- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Цилиндр и конус. Усеченный конус. Решение задач
Содержание
- 1. Презентация Цилиндр и конус. Усеченный конус. Решение задач
- 2. Цель урока сегодня:Рассмотреть понятие цилиндра, конуса, усеченного
- 3. Окружность -Окружностью называется геометрическая фигура,состоящая из всех
- 4. Примеры цилиндровСлово цилиндр - означает от греческого слова “валик”, “каток”.
- 5. Конусные фигуры в бытуФормы конуса в профессии «Повара, кондитера»
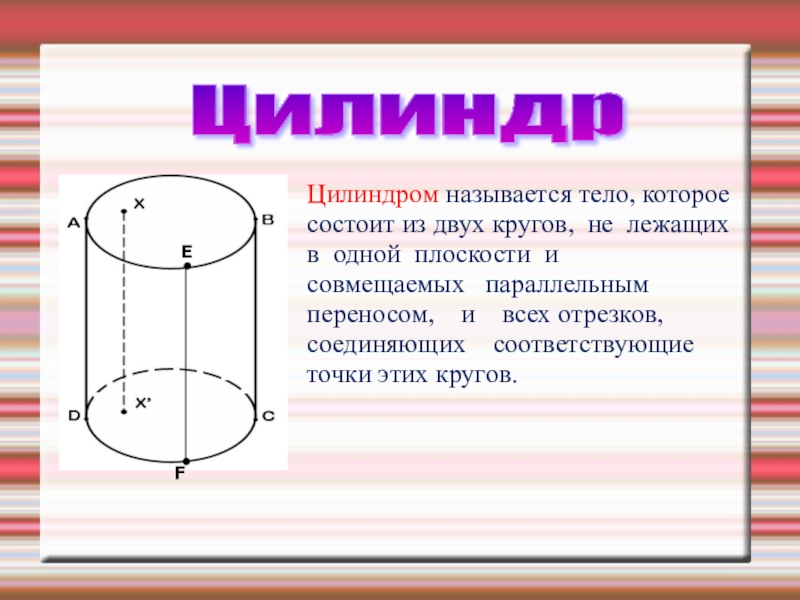
- 6. Цилиндром называется тело, которое состоит из двух
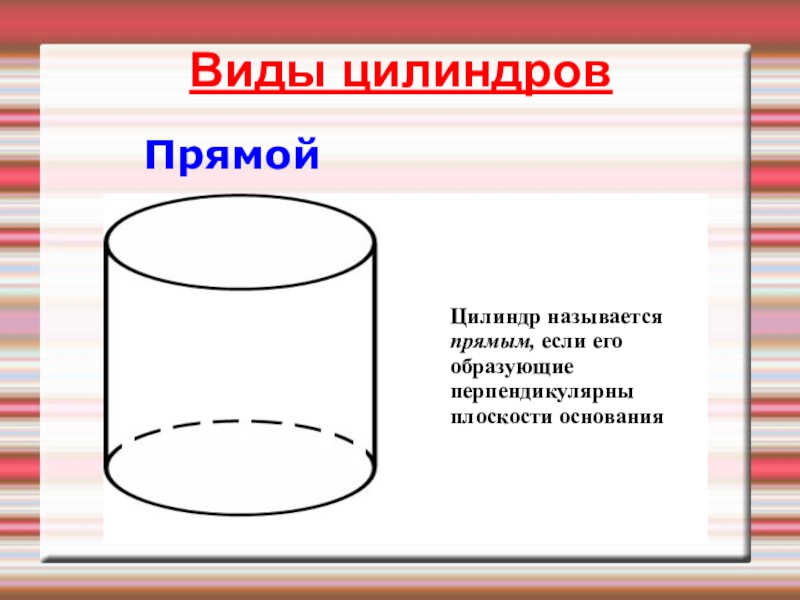
- 7. ПрямойЦилиндр называется прямым, если его образующие перпендикулярны плоскости основанияВиды цилиндров
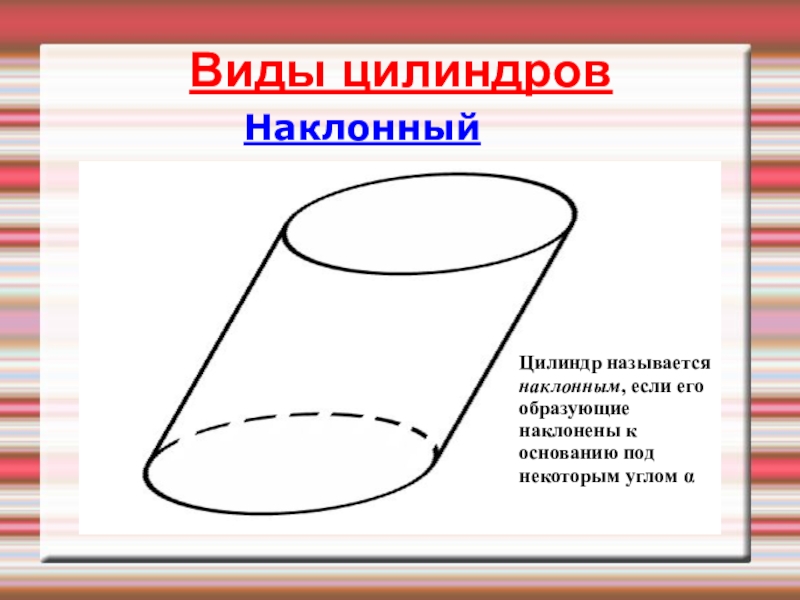
- 8. НаклонныйЦилиндр называется наклонным, если его образующие наклонены к основанию под некоторым углом αВиды цилиндров
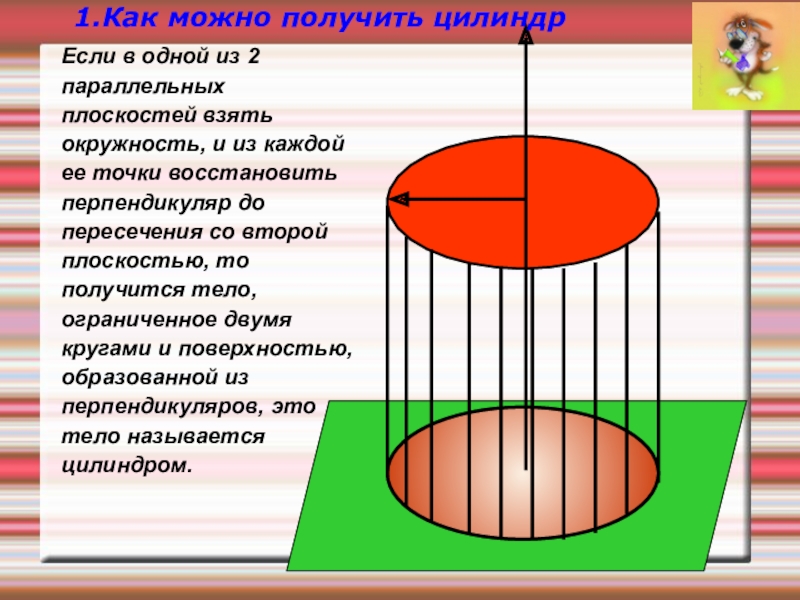
- 9. Если в одной из 2 параллельных плоскостей
- 10. А можно так получить цилиндрВращением прямоугольника вокруг
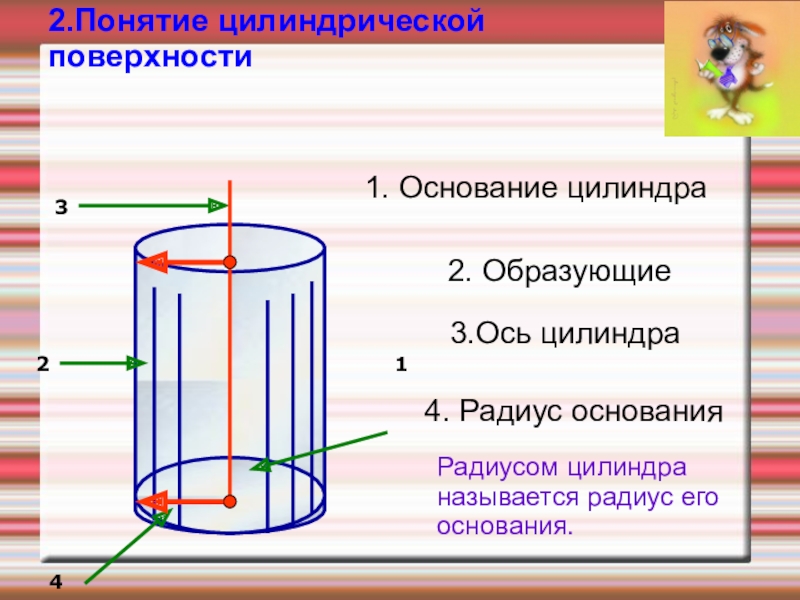
- 11. 2.Понятие цилиндрической поверхности12341. Основание цилиндра2. Образующие3.Ось цилиндра4. Радиус основания4Радиусом цилиндра называется радиус его основания.
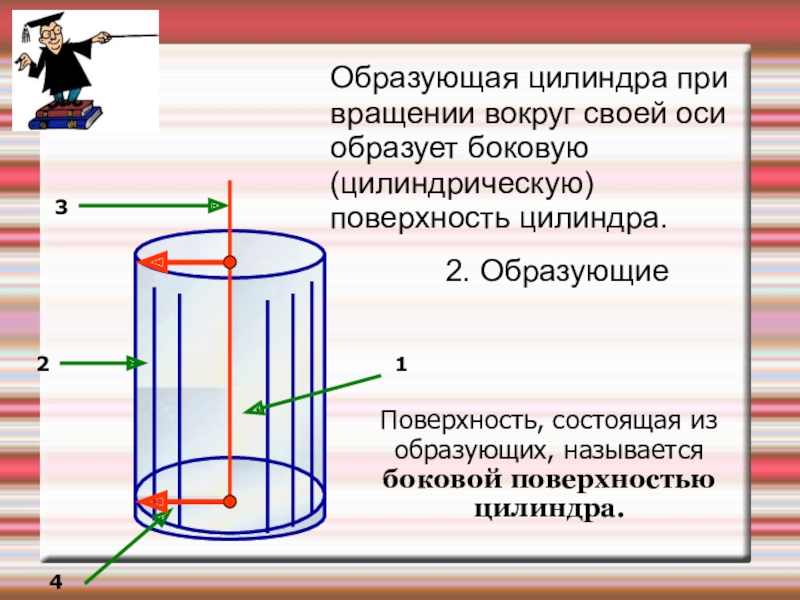
- 12. Образующая цилиндра при вращении вокруг своей оси
- 13. Понятие цилиндрической поверхности, цилиндра
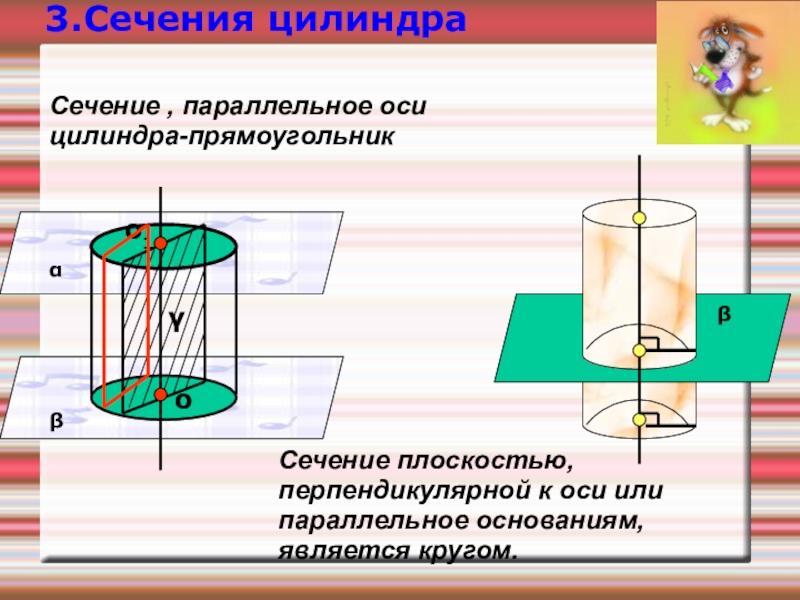
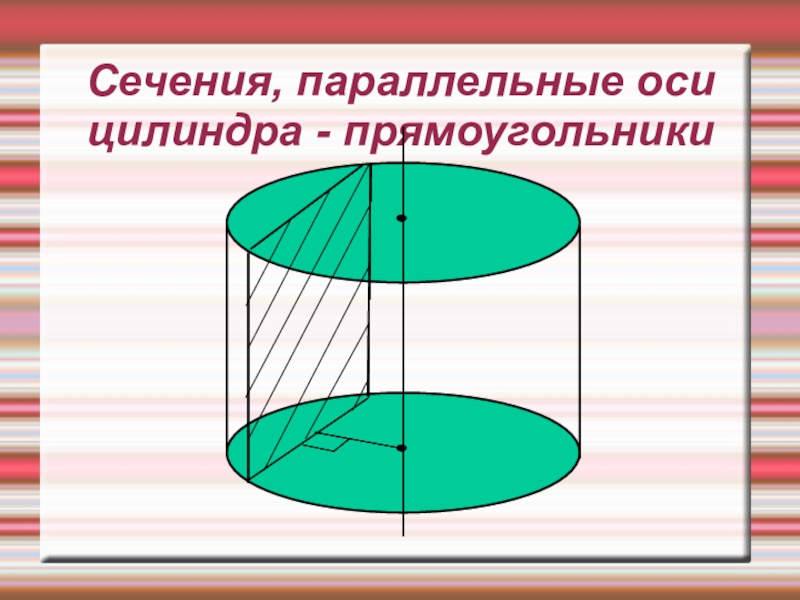
- 14. Сечение плоскостью, перпендикулярной к оси или параллельное основаниям, является кругом.βαβоо1γ3.Сечения цилиндраСечение , параллельное оси цилиндра-прямоугольник
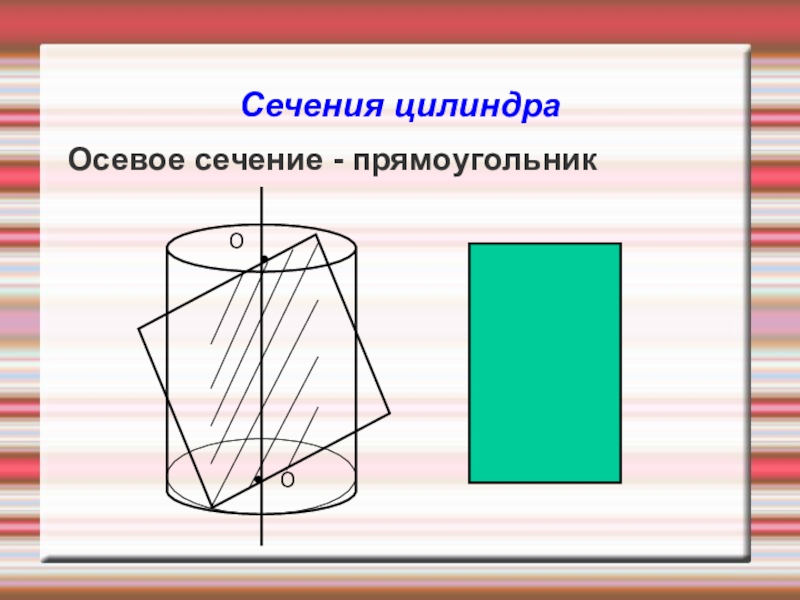
- 15. Сечения цилиндра Осевое сечение - прямоугольникОО
- 16. Сечения, параллельные оси цилиндра - прямоугольники
- 17. Разверткой боковой поверхности цилиндра является прямоугольник со
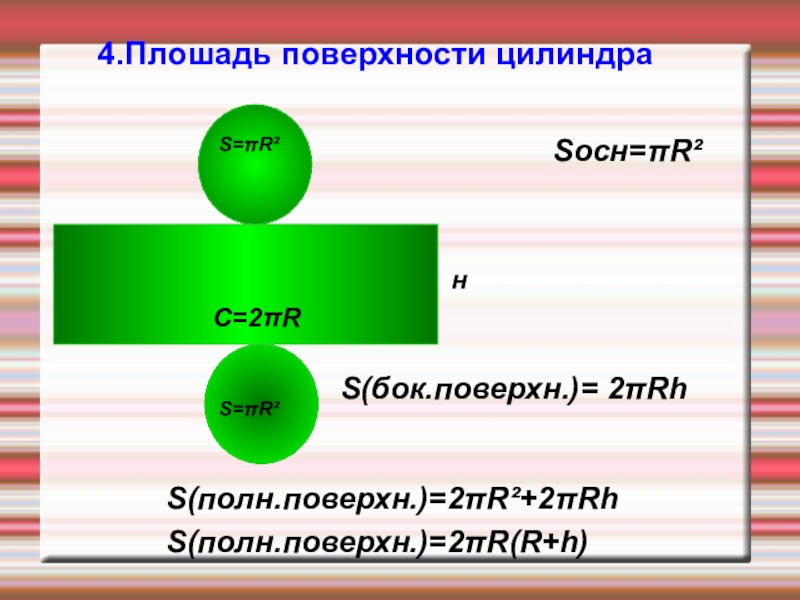
- 18. 4.Плошадь поверхности цилиндраS(полн.поверхн.)=2πR(R+h)S(бок.поверхн.)= 2πRhSосн=πR²нС=2πRS=πR²S=πR²S(полн.поверхн.)=2πR²+2πRh
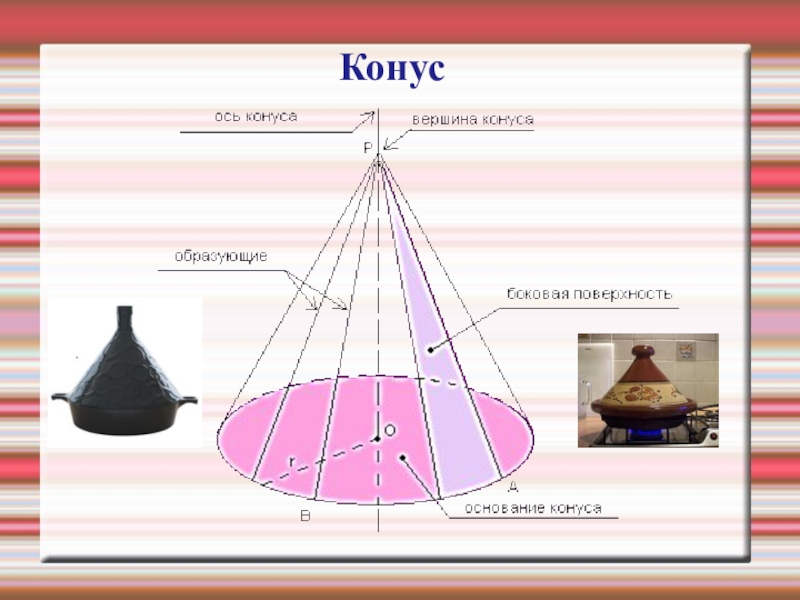
- 19. Конус -это тело, ограниченное конической поверхностью и кругом с границей L
- 20. Конус
- 21. Конус получен вращением прямоугольного треугольника АВС вокруг катета АВ
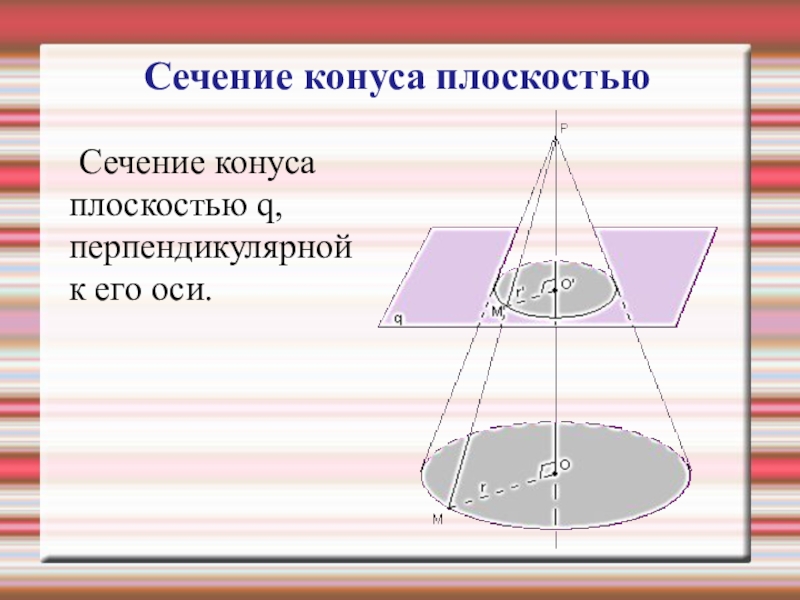
- 22. Осевое сечение конуса Если секущая
- 23. Сечение конуса плоскостью q, перпендикулярной
- 24. Площадь поверхности конусаЗа площадь боковой поверхности конуса
- 25. Конус можно рассмотреть в различных предметах, начиная с обычного мороженого и заканчивая техникой .
- 26. Нахождение конуса в природе В природе мы
- 27. «Конусами» называется семейство морских моллюсков. Конусов свыше
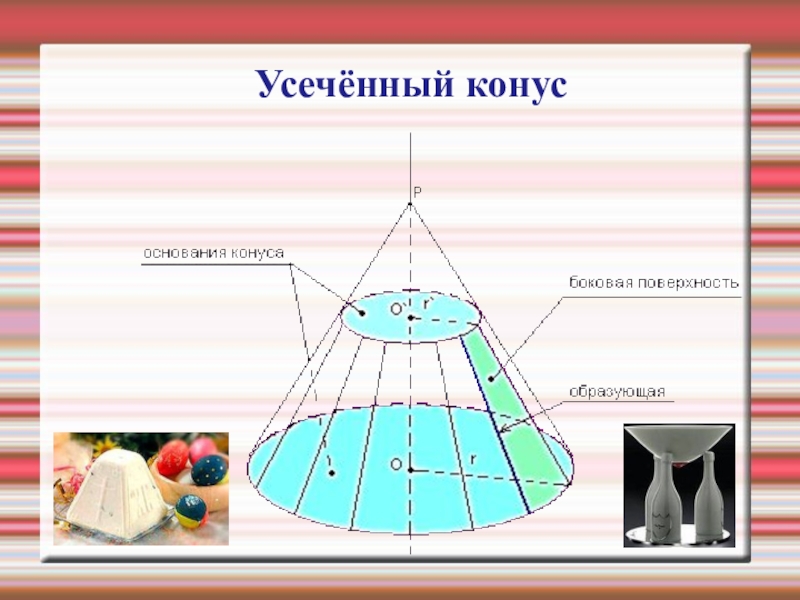
- 28. Усечённый конус
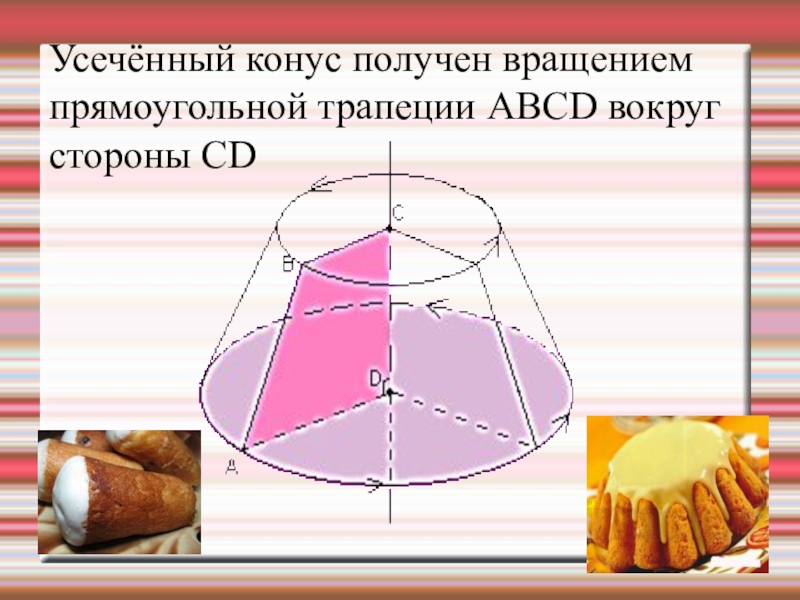
- 29. Усечённый конус получен вращением прямоугольной трапеции АВСD вокруг стороны CD
- 30. Площадь боковой поверхности усечённого конусаравна произведению полусуммы
- 31. Задача №1:Найти площадь полной поверхности цилиндраАВС45ºАВС- прямоугольныйАВС- равнобедренный5ВС=АС=5r=2,5S=2π·2,5(5 + 2,5)= 5π·7,5 = 37,5πАВСS=2πr(h+r)АВСАВСrРешение задач
- 32. Задача №2:Площадь осевого сечения цилиндра равна
- 33. Решение задач на нахождение площадей боковой и полной поверхности конуса, усечённого конуса rlРешение задач
- 34. Решение задач на нахождение площадей боковой и
- 35. Подведем итог по теме:Какая фигура называется цилиндром?
- 36. Подведем итог по теме:10.Что такое конус?11.При вращении
- 37. Спасибо за внимание!
Цель урока сегодня:Рассмотреть понятие цилиндра, конуса, усеченного конуса, их элементов, научиться решению задач по нахождению элементов цилиндра, конуса. Рассмотреть понятие площади боковой поверхности и полной поверхности цилиндра, конуса и усеченного конуса, научиться решать задачи на
Слайд 1
«Цилиндр и конус.
Усеченный конус.
Решение задач »
Разработала: Преподаватель математики Зайцева Светлана Егоровна.
Слайд 2Цель урока сегодня:
Рассмотреть понятие цилиндра, конуса, усеченного конуса, их элементов, научиться
решению задач по нахождению элементов цилиндра, конуса.
Рассмотреть понятие площади боковой поверхности и полной поверхности цилиндра, конуса и усеченного конуса, научиться решать задачи на их нахождение
Рассмотреть понятие площади боковой поверхности и полной поверхности цилиндра, конуса и усеченного конуса, научиться решать задачи на их нахождение
Слайд 3
Окружность -
Окружностью называется геометрическая фигура,состоящая из всех точек плоскости, расположенных на
заданном расстоянии от данной точки
Треугольник -
Геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и соединяющих их отрезков
Слайд 6Цилиндром называется тело, которое состоит из двух кругов, не лежащих в
одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Цилиндр
Слайд 7Прямой
Цилиндр называется прямым, если его образующие перпендикулярны плоскости основания
Виды цилиндров
Слайд 8Наклонный
Цилиндр называется наклонным, если его образующие наклонены к основанию под некоторым
углом α
Виды цилиндров
Слайд 9
Если в одной из 2 параллельных плоскостей взять окружность, и из
каждой ее точки восстановить перпендикуляр до пересечения со второй плоскостью, то получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров, это тело называется цилиндром.
1.Как можно получить цилиндр
Слайд 10
А можно так получить цилиндр
Вращением прямоугольника вокруг одной из его сторон
Круги,
лежащие в параллельных плоскостях, называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей оснований –называются образующими цилиндра.
Слайд 112.Понятие цилиндрической
поверхности
1
2
3
4
1. Основание цилиндра
2. Образующие
3.Ось цилиндра
4. Радиус основания
4
Радиусом цилиндра называется
радиус его основания.
Слайд 12Образующая цилиндра при вращении вокруг своей оси образует боковую (цилиндрическую) поверхность
цилиндра.
1
2
3
4
4
2. Образующие
Поверхность, состоящая из образующих, называется боковой поверхностью цилиндра.
Слайд 14Сечение плоскостью, перпендикулярной к оси или параллельное основаниям, является кругом.
β
α
β
о
о1
γ
3.Сечения цилиндра
Сечение
, параллельное оси цилиндра-прямоугольник
Слайд 17Разверткой боковой поверхности цилиндра является прямоугольник со сторонами Н и С,
где Н – высота цилиндра, а С – длина окружности основания.
н
С=2πR
S=πR²
S=πR²
Слайд 184.Плошадь поверхности цилиндра
S(полн.поверхн.)=2πR(R+h)
S(бок.поверхн.)= 2πRh
Sосн=πR²
н
С=2πR
S=πR²
S=πR²
S(полн.поверхн.)=2πR²+2πRh
Слайд 22Осевое сечение конуса
Если секущая плоскость проходит через ось
конуса, то сечение представляет собой равнобедренный треугольник, основание которого- диаметр основания конуса, а боковые стороны- образующие конуса. Это сечение- осевое.
Слайд 24
Площадь поверхности конуса
За площадь боковой поверхности конуса принимается площадь её развертки.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. S=πrl
Площадь полной поверхности конуса- сумма площадей боковой поверхности и основания.S=πr(l+r)
Слайд 25 Конус можно рассмотреть в различных предметах, начиная с обычного мороженого
и заканчивая техникой .
Слайд 26Нахождение конуса в природе
В природе мы часто встречаем конус. Например, в
песчаной пустыне Сахаре, где сами холмы представляют собой конус.
Слайд 27«Конусами» называется семейство морских моллюсков. Конусов свыше 500 видов. Живут в
тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи. Раковины используются как украшения, сувениры.
Слайд 30Площадь боковой поверхности усечённого конуса
равна произведению полусуммы длин окружностей оснований на
образующую:
S = π (r + r₁) l
S = π (r + r₁) l
Слайд 31
Задача №1:Найти площадь полной поверхности цилиндра
А
В
С
45º
АВС
- прямоугольный
АВС
- равнобедренный
5
ВС=АС=5
r=2,5
S=2π·2,5(5 + 2,5)= 5π·7,5
= 37,5π
АВС
S=2πr(h+r)
АВС
АВС
r
Решение задач
Слайд 32
Задача №2:Площадь осевого сечения цилиндра равна 10 м2, а площадь
основания равна 5 м2. Найдите высоту цилиндра.
А
В
С
D
O
O1
R
H
R=
H=
м
Слайд 33Решение задач на нахождение площадей боковой и полной поверхности конуса, усечённого
конуса
r
l
Решение задач
Слайд 34Решение задач на нахождение площадей боковой и полной поверхности конуса, усечённого
конуса.
Задача 2. Сколько потребуется посыпки на торт «Муравейник» диаметром основания 26 см, и высотой 15 см, если на каждый квадратный сантиметр ее требуется 3 г.
Рекомендации к решению: Торт «Муравейник» имеет форму конуса, вся посыпка представляет собой боковую поверхность. Зная диаметр найдем радиус, зная высоту и радиус найдем образующую, а затем и площадь боковой поверхности, т.е. площадь поверхности посыпки.
Слайд 35Подведем итог по теме:
Какая фигура называется цилиндром?
Почему цилиндр называют телом
вращения?
Назовите виды цилиндров?
Назовите элементы цилиндра.
Что представляет собой развертка цилиндра?
Как найти площадь боковой поверхности цилиндра?
Как найти площадь полной поверхности цилиндра?
Назовите основные виды сечений цилиндра. Какая фигура получается в каждом случае?
Приведите примеры использования цилиндров.
Назовите виды цилиндров?
Назовите элементы цилиндра.
Что представляет собой развертка цилиндра?
Как найти площадь боковой поверхности цилиндра?
Как найти площадь полной поверхности цилиндра?
Назовите основные виды сечений цилиндра. Какая фигура получается в каждом случае?
Приведите примеры использования цилиндров.
Слайд 36Подведем итог по теме:
10.Что такое конус?
11.При вращении какой фигуры получается конус,
усеченный конус?
12.Как надо пересечь конус плоскостью, чтобы в сечении получить: а) равнобедренный треугольник, б) круг.
13.Как получить усеченный конус из полного конуса?
14.Назовите основные элементы конуса, усеченного конуса.
15.Сформулируйте теорему Пифагора.
16.Как находится площадь:
а) боковой поверхности конуса?
б)Полной поверхности конуса?
в)Полной поверхности усеченного конуса?
12.Как надо пересечь конус плоскостью, чтобы в сечении получить: а) равнобедренный треугольник, б) круг.
13.Как получить усеченный конус из полного конуса?
14.Назовите основные элементы конуса, усеченного конуса.
15.Сформулируйте теорему Пифагора.
16.Как находится площадь:
а) боковой поверхности конуса?
б)Полной поверхности конуса?
в)Полной поверхности усеченного конуса?
