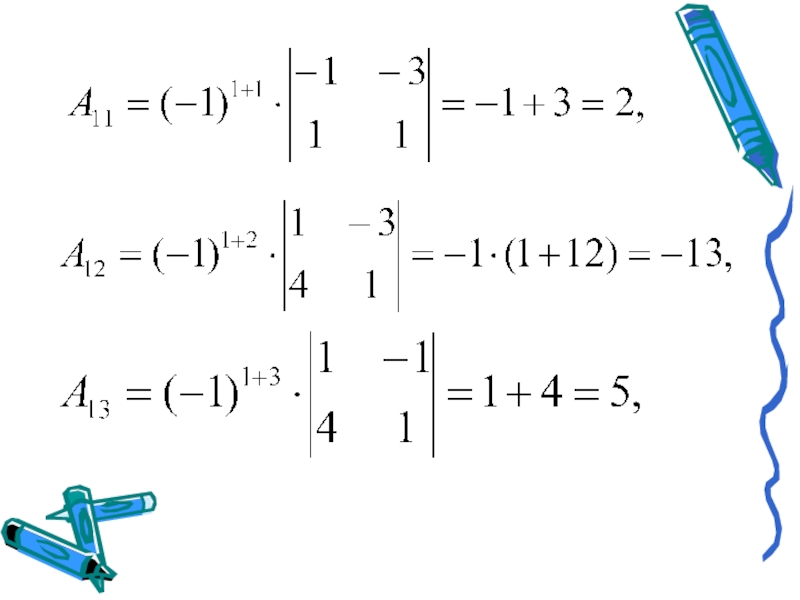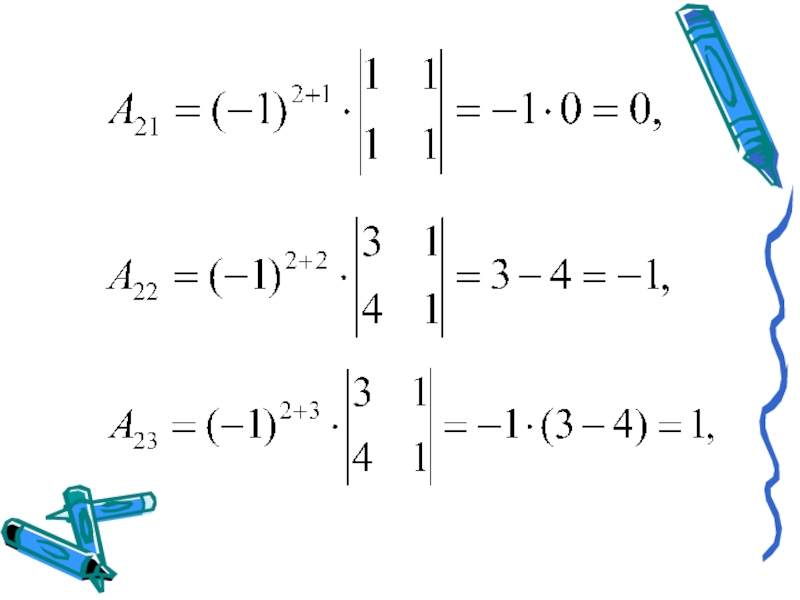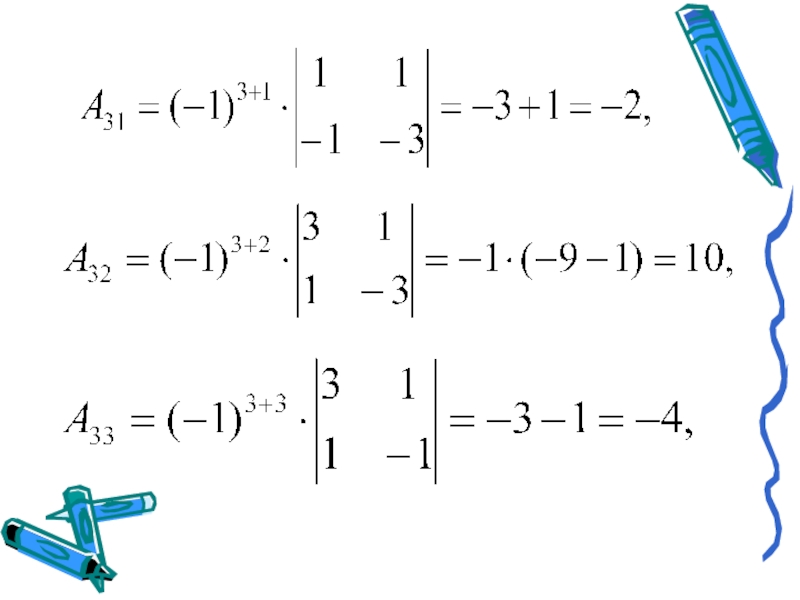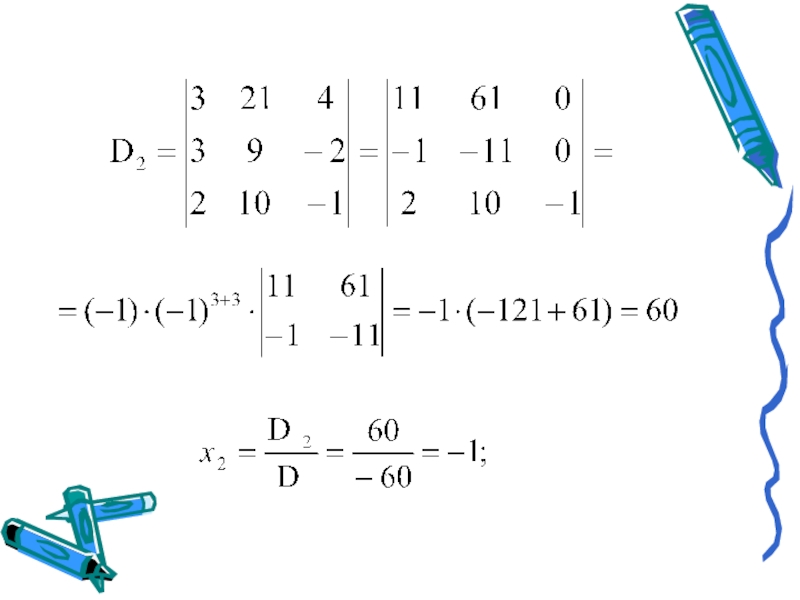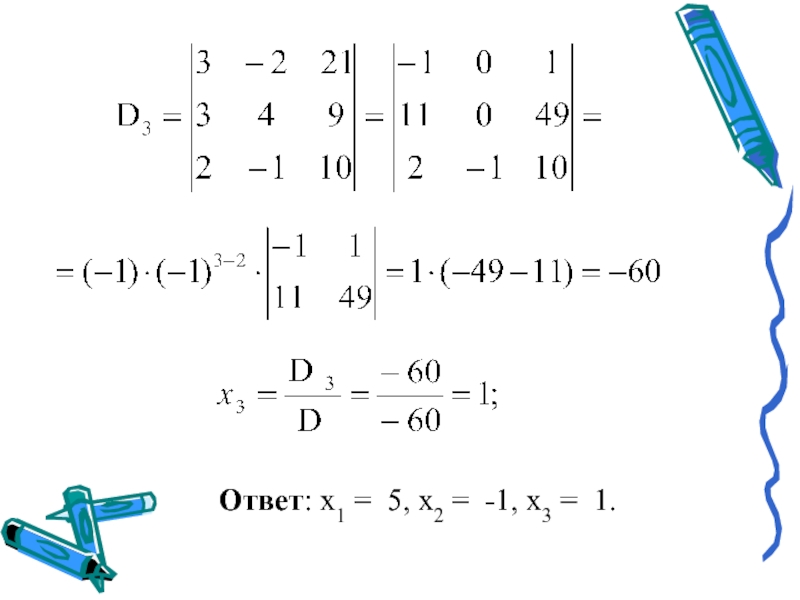Презентация, доклад Решение систем линейных уравнений

Содержание

1. Презентация Решение систем линейных уравнений
2. Решение систем линейных уравнений
3. Уравнение
4. Методы решения:1)Матричный метод решения.2)Метод Крамера.3) Метод Гаусса
5. 1)Матричный метод решения.Запишем заданную систему в матричном
6. 1)Матричный метод решения.Поэтому, чтобы найти неизвестную матрицу Х надо
7. Пример 1. Решить систему матричным способом.Решение: Решим
8. Т.к. матрица невырожденная (Δ= – 2), то X = A-1B.
9. Слайд 9
10. Слайд 10
11. Слайд 11
12. Тогда A-1 = Получим X = A-1B
13. 2)Метод Крамера.Метод Крамера (теорема Крамера) — способ
14. где вместо -го столбца стоит
15. D 0, значит, система
16. Слайд 16
17. Ответ: x1 = 5, x2 = -1, x3 = 1.
18. 3) Метод Гаусса Метод Гаусса - Метод
19. Пример 3. Исследовать систему и решить ее
20. Слайд 20
21. (привели матрицу (A,B) к матрице (
22.
23. ⇒ решение найдено верно.
24. еАРНВСТВОНРАЕЛ
25. ЦА ЬТР=ТДНАОДИН1ДР
26. ТЬЕАТЬЕ21,2ДВНАДЦАПЛЯ
27. РТЬНАЦАРДДЬТПЯТ
28. ОСИЛЧОСИЛАЧ5,2,1,3,
29. 2,3,АДТоТСАТОКДЕЛЬОКЗАТВОСТ
30. Спасибо за внимание!

Решение систем линейных уравнений

Главная
Математика
Презентация Решение систем линейных уравнений

Слайд 1Д
ЙНИК
ЧА
А

Д

ЗА
А

Слайд 2Решение систем линейных уравнений

Слайд 3Уравнение

Слайд 4Методы решения:
1)Матричный метод решения.
2)Метод Крамера.
3) Метод Гаусса

Слайд 51)Матричный метод решения.
Запишем заданную систему в матричном виде:
АХ=В,
где А

– основная матрица коэффициентов системы;
Х – матрица-столбец неизвестных;
В – матрица-столбец свободных членов.
Если матрица А невырожденная (det А=Δ≠0), то тогда с помощью операций над матрицами выразим неизвестную матрицу Х . Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому умножив последнее равенство на матрицу слева:

1)Матричный метод решения.Запишем заданную систему в матричном виде: АХ=В, где А – основная матрица коэффициентов системы; Х

Слайд 61)Матричный метод решения.
Поэтому, чтобы найти неизвестную матрицу Х надо найти обратную матрицу к

матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.

1)Матричный метод решения.Поэтому, чтобы найти неизвестную матрицу Х надо найти обратную матрицу к матрице системы и умножить ее справа

Слайд 7Пример 1. Решить систему матричным способом.

Решение: Решим систему линейных уравнений
матричным

методом. Обозначим

Тогда данную систему можно записать в виде: АХ=В.

Слайд 8

Т.к. матрица невырожденная (Δ= – 2), то X = A-1B.

Слайд 9

Слайд 10

Слайд 11

Слайд 12Тогда A-1 =

Получим X = A-1B =

Ответ: х1 = –1,

х2 = 4, х3 = 1.

Слайд 132)Метод Крамера.
Метод Крамера (теорема Крамера) — способ решения квадратных СЛАУ с

ненулевым определителем основной матрицы.
Теорема Крамера. Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера:

где

- определитель матрицы системы,

2)Метод Крамера.Метод Крамера (теорема Крамера) — способ решения квадратных СЛАУ с ненулевым определителем основной матрицы.Теорема Крамера. Если определитель

Слайд 14где вместо
-го столбца стоит

столбец правых частей.

Пример 2. Решить систему по формулам Крамера.

Решение: Решим систему по формулам Крамера.

где вместо -го столбца стоит столбец правых частей.Пример 2. Решить

Слайд 15D 0, значит, система имеет

единственное решение.

Слайд 16

Слайд 17

Ответ: x1 = 5, x2 = -1, x3 = 1.

Слайд 183) Метод Гаусса
Метод Гаусса - Метод последовательного исключения неизвестных. Метод Гаусса

включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный - методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.

3) Метод Гаусса Метод Гаусса - Метод последовательного исключения неизвестных. Метод Гаусса включает в себя прямой (приведение расширенной

Слайд 19Пример 3. Исследовать систему и решить ее методом Гаусса, если она

совместна

Решение: Дана неоднородная линейная система из 4-х уравнений с 4-мя неизвестными (m=n=4).
1) Определим, совместна или нет система (*). Вычисляем для этого ранги расширенной и основной матриц системы: Rg(A,B) и RgA.

Слайд 20

Слайд 21(привели матрицу (A,B) к матрице ( ),

имеющую ступенчатую форму).
Итак, Rg(A, B) = Rg( ) = 4, RgA= Rg = 4 ⇒ RgA= Rg(A,B) = 4. Следовательно система (*) совместна. Т.к. Rg A= n (n = 4) ⇒ система имеет единственное решение.
Найдем все решения системы (*). Для этого перейдем
к следующей эквивалентной системе.