- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по темеАксиомы стереометрии
Содержание
- 1. Презентация по темеАксиомы стереометрии
- 2. ГеометрияПланиметрияСтереометрия stereos телесный, твердый, объемный, пространственный
- 3. Стереометрия.Раздел геометрии, в котором изучаются свойства фигур в пространстве.Основные фигуры в пространстве:АТочка.аПрямая.Плоскость.
- 4. 1. Точки. Их обозначают латинскими заглавными буквами:
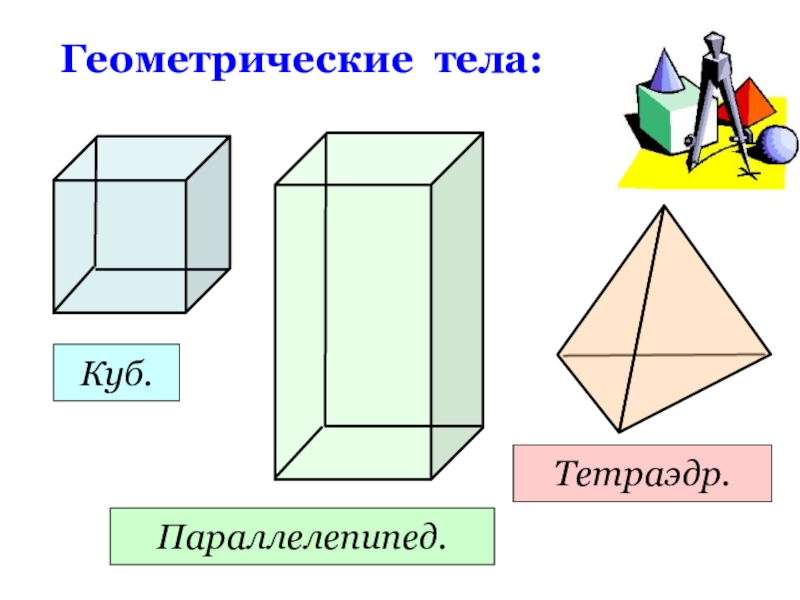
- 5. Геометрические тела:Куб.Параллелепипед.Тетраэдр.
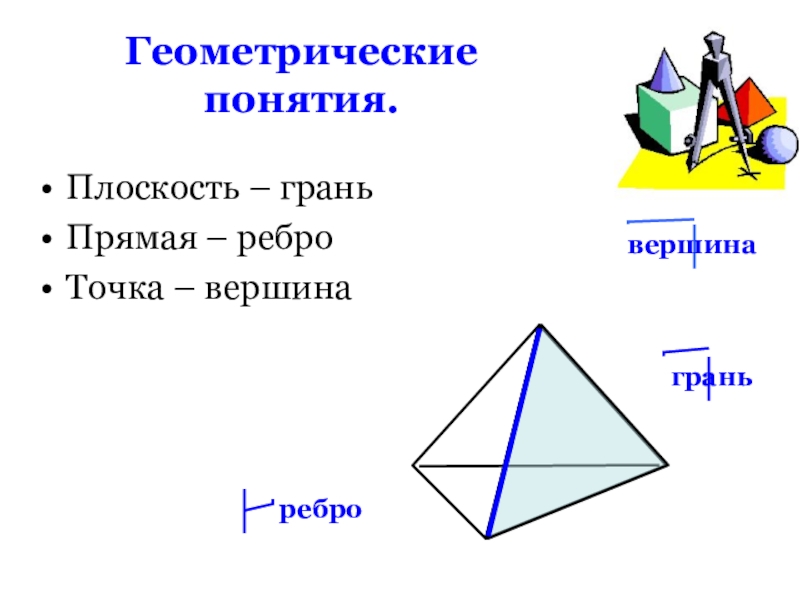
- 6. Геометрические понятия.Плоскость – граньПрямая – реброТочка – вершинавершинаграньребро
- 7. Аксиома(от греч. axíõma – принятие положения)исходное положение научной теории, принимаемое без доказательства
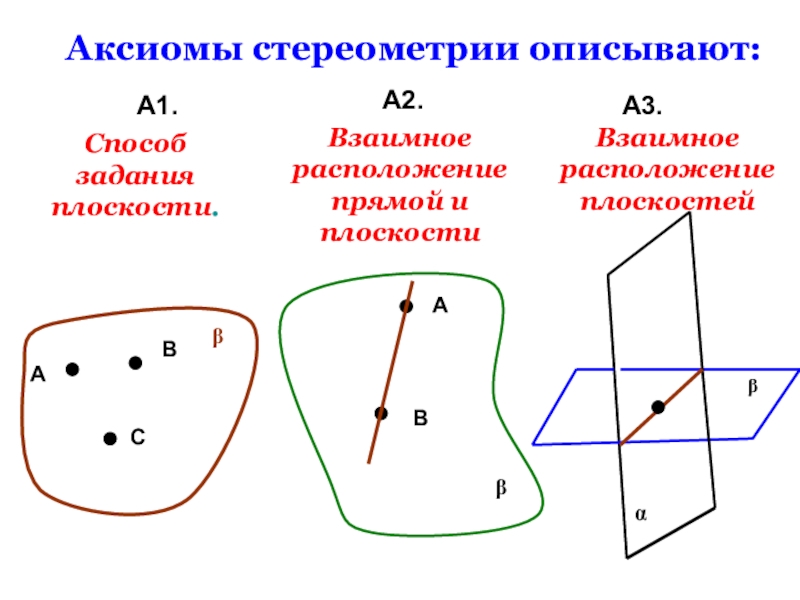
- 8. Аксиомы стереометрии описывают:А1.А2. А3. АВСβСпособ задания плоскости.βАВВзаимное расположение прямой и плоскостиαβВзаимное расположение плоскостей
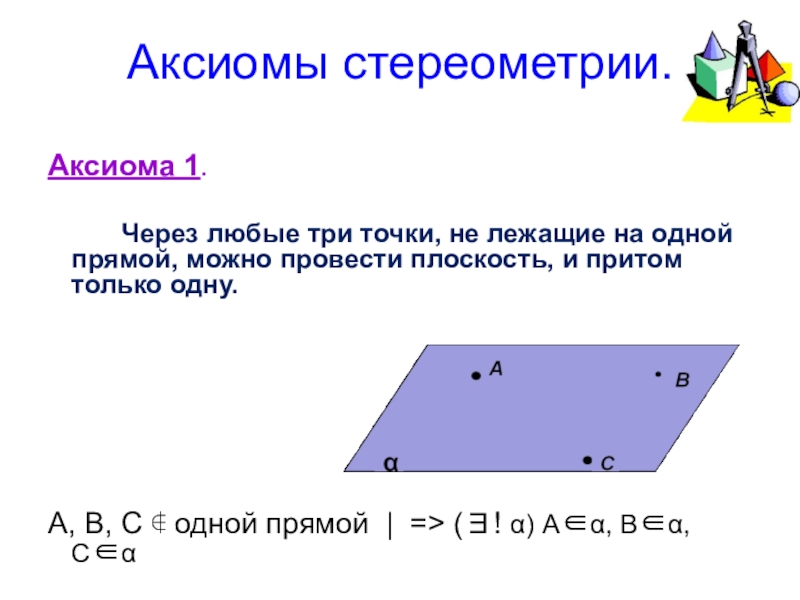
- 9. Аксиома 1.
- 10. A ∉ a | => (∃! β)
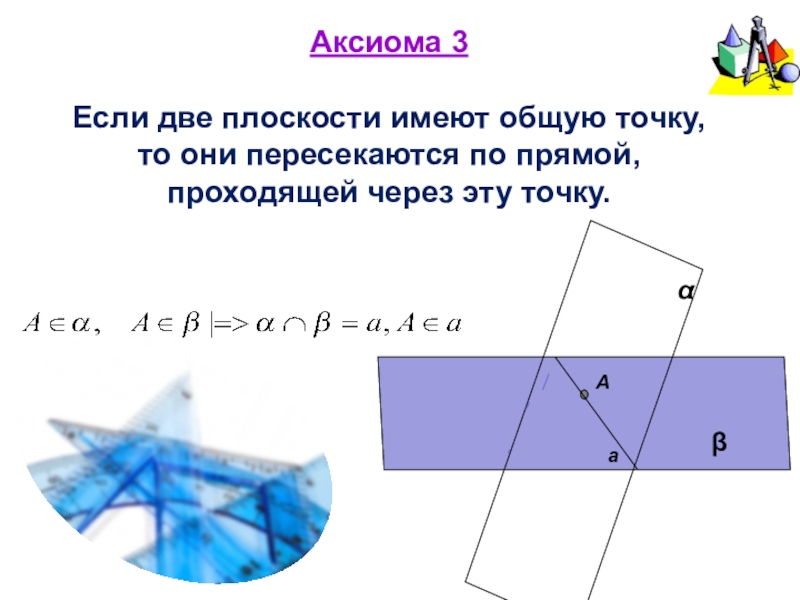
- 11. Аксиома 3 Если две плоскости имеют
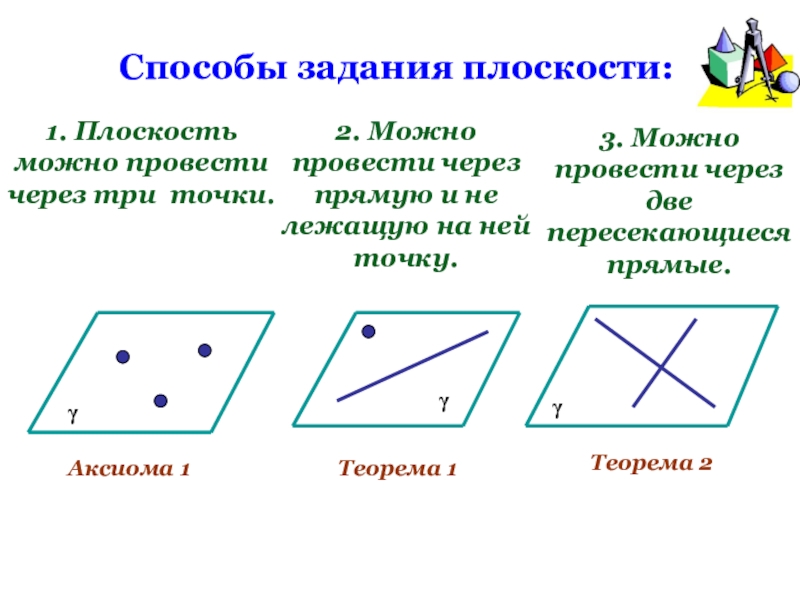
- 12. Способы задания плоскости:1. Плоскость можно провести через
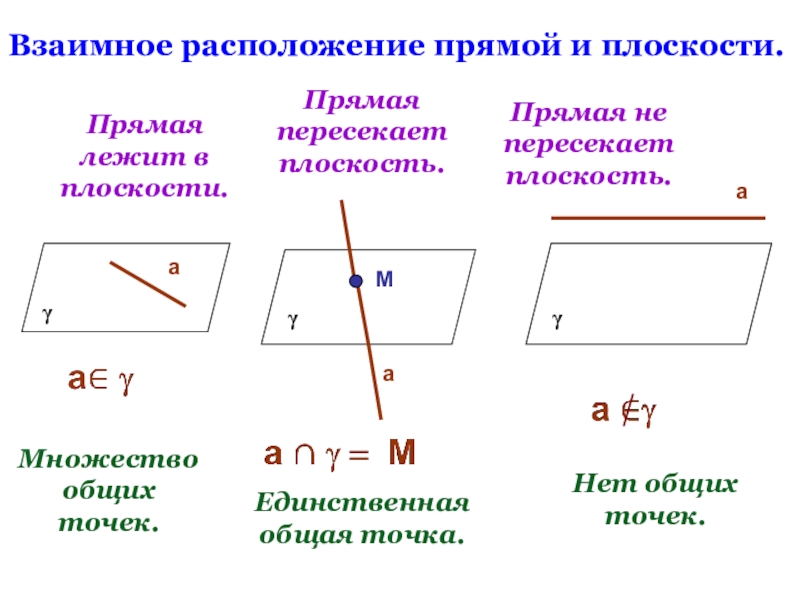
- 13. Взаимное расположение прямой и плоскости.Прямая лежит в
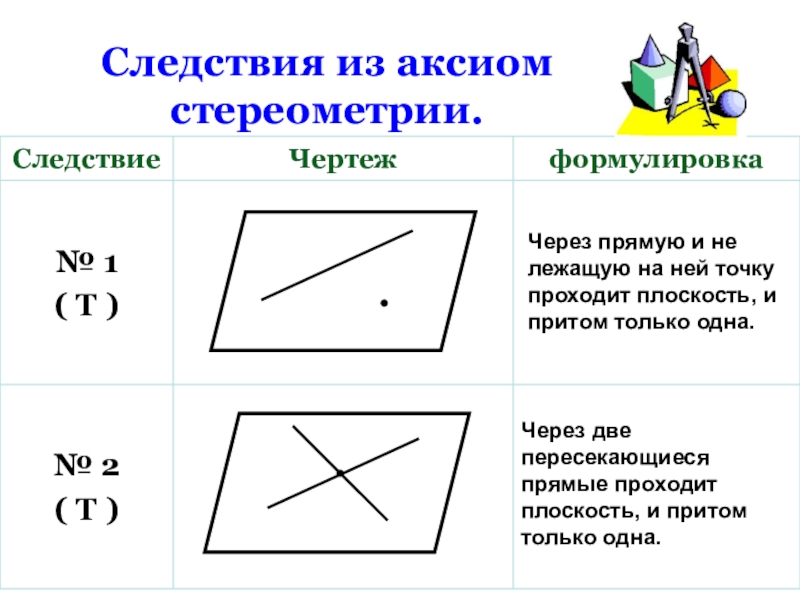
- 14. Следствия из аксиом стереометрии.Через прямую и не
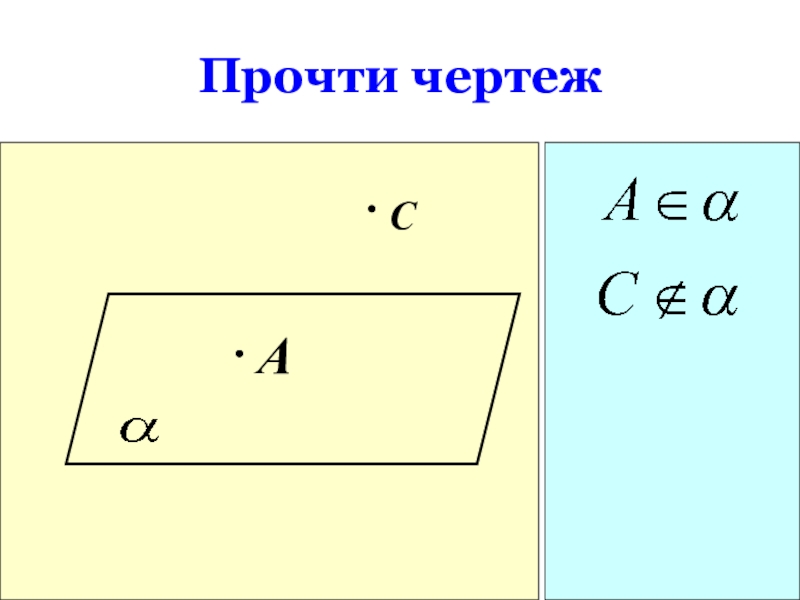
- 15. Прочти чертежAС
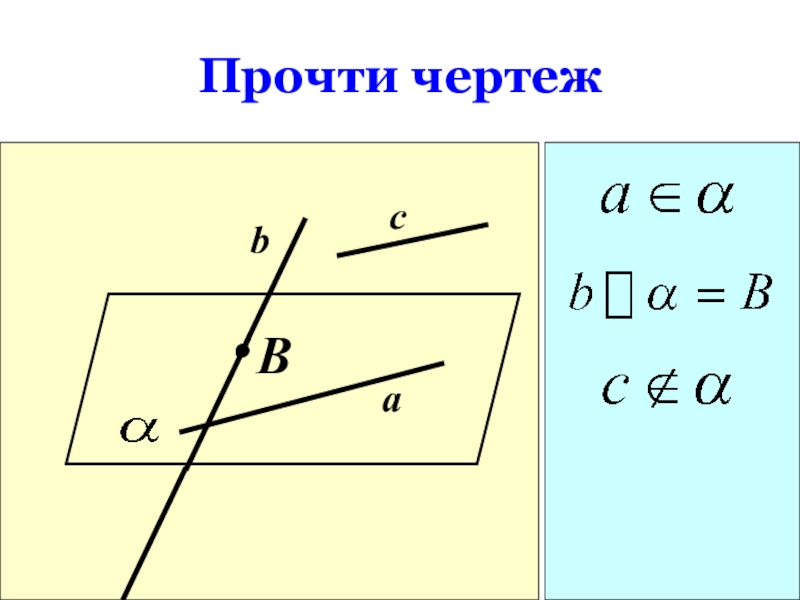
- 16. Прочти чертежBcba
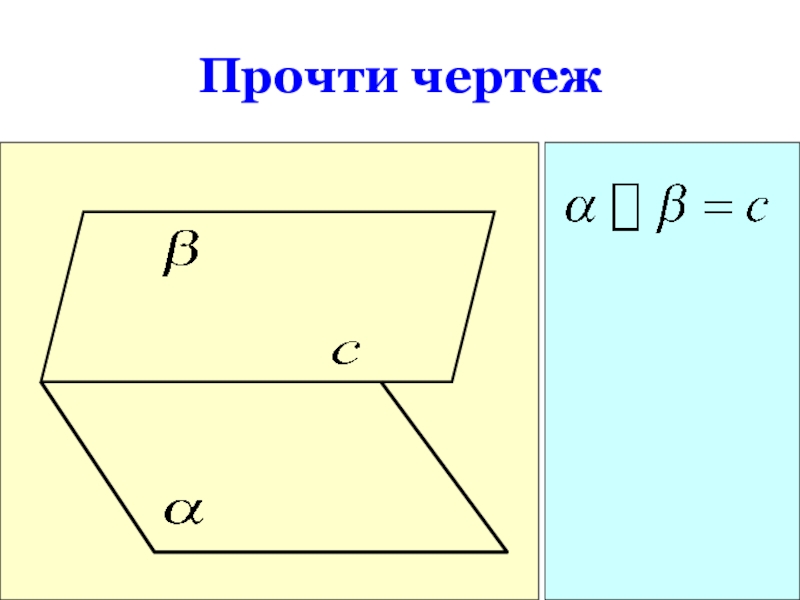
- 17. Прочти чертеж
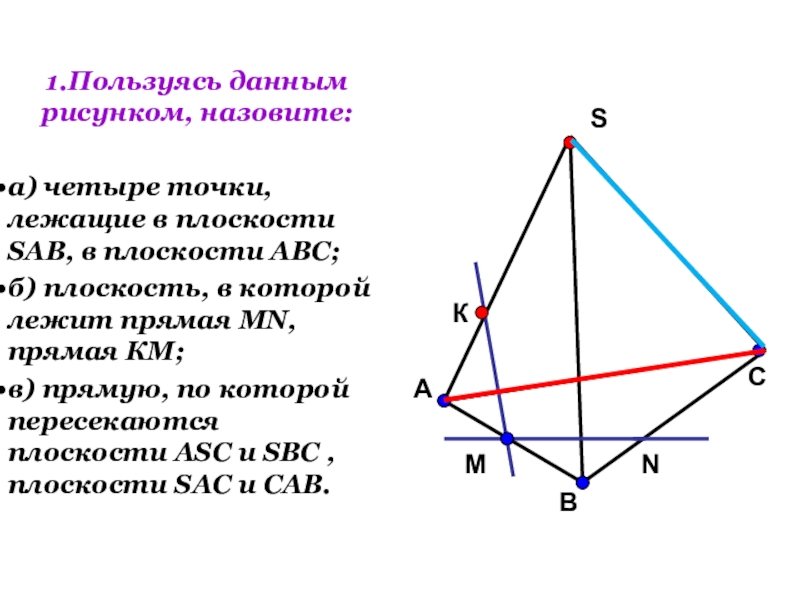
- 18. 1.Пользуясь данным рисунком, назовите:а) четыре точки, лежащие
- 19. 2.Пользуясь данным рисунком, назовите:а) две плоскости, содержащие
- 20. 3.Пользуясь данным рисунком, назовите:а) три плоскости, содержащие прямую В1С; б) три плоскости, содержащие прямую АВ1;
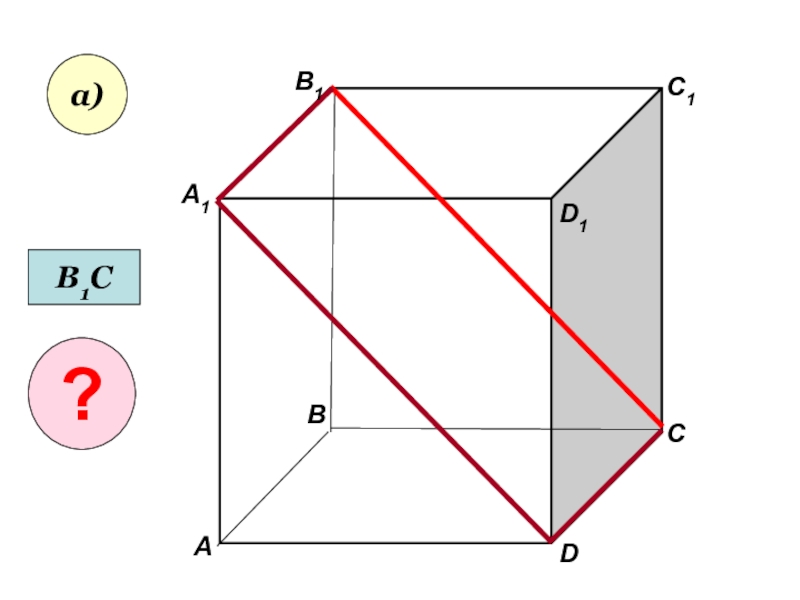
- 21. АА1ВВ1СD1DC1а)В1С?
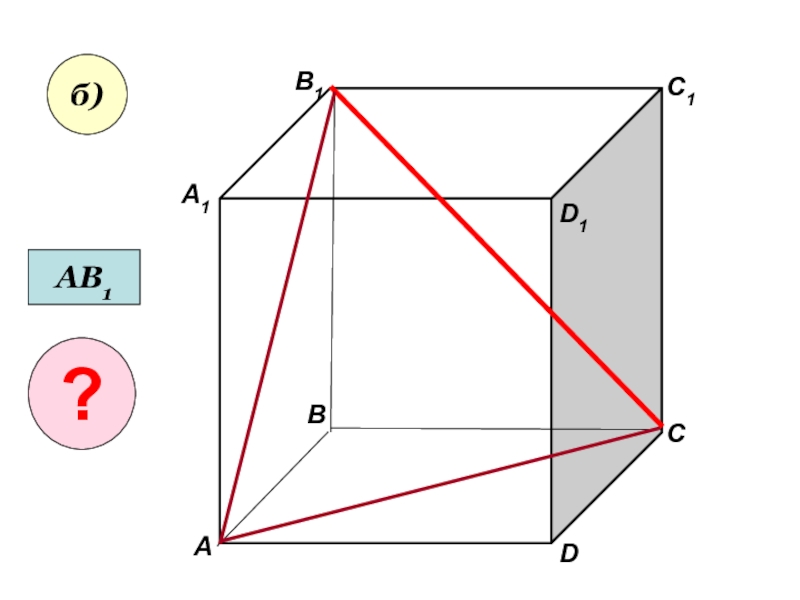
- 22. АА1ВВ1СD1DC1б)АВ1?
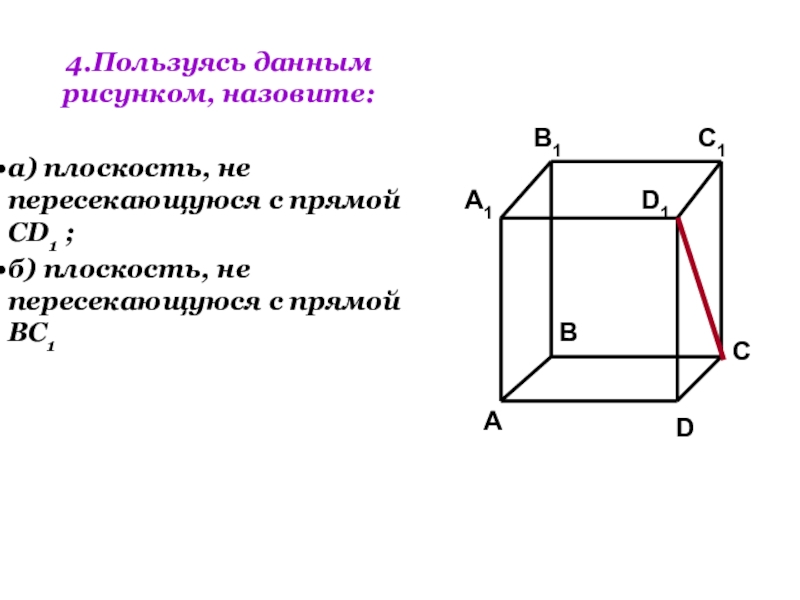
- 23. 4.Пользуясь данным рисунком, назовите:а) плоскость, не пересекающуюся
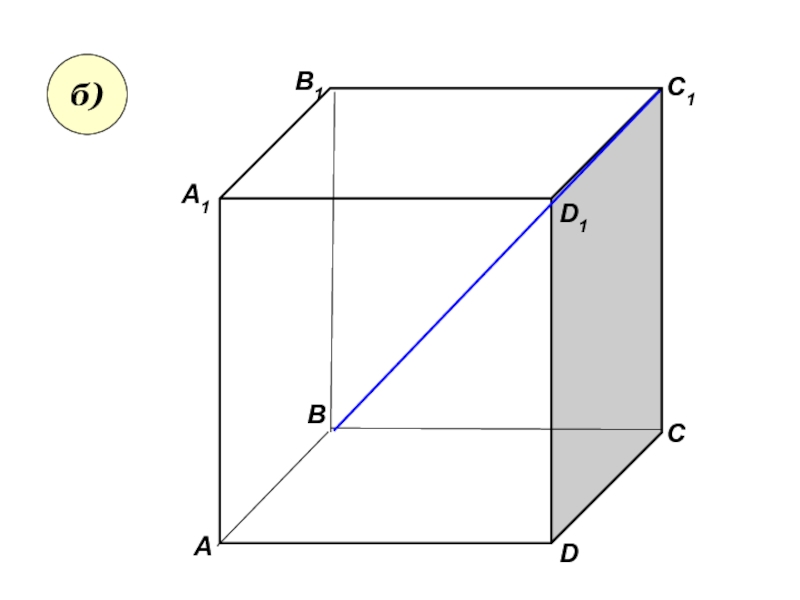
- 24. АА1ВВ1СD1DC1б)
- 25. Спасибо за внимание!
ГеометрияПланиметрияСтереометрия stereos телесный, твердый, объемный, пространственный
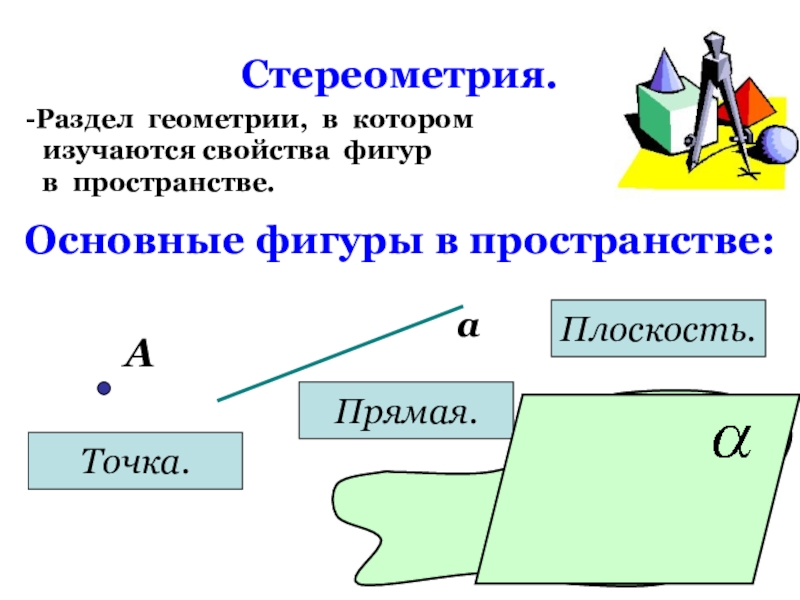
Слайд 3Стереометрия.
Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные
фигуры в пространстве:
А
Точка.
а
Прямая.
Плоскость.
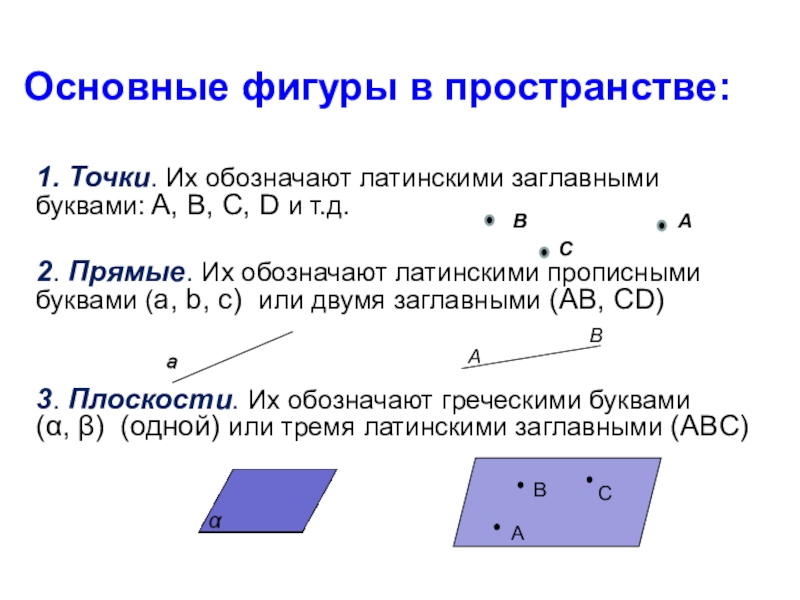
Слайд 41. Точки. Их обозначают латинскими заглавными буквами: A, B, C, D
и т.д.
2. Прямые. Их обозначают латинскими прописными буквами (a, b, c) или двумя заглавными (AB, CD)
3. Плоскости. Их обозначают греческими буквами (α, β) (одной) или тремя латинскими заглавными (ABC)
2. Прямые. Их обозначают латинскими прописными буквами (a, b, c) или двумя заглавными (AB, CD)
3. Плоскости. Их обозначают греческими буквами (α, β) (одной) или тремя латинскими заглавными (ABC)
Основные фигуры в пространстве:
Слайд 7Аксиома
(от греч. axíõma – принятие положения)
исходное положение научной теории, принимаемое без
доказательства
Слайд 8Аксиомы стереометрии описывают:
А1.
А2.
А3.
А
В
С
β
Способ задания плоскости.
β
А
В
Взаимное расположение прямой и плоскости
α
β
Взаимное
расположение плоскостей
Слайд 9Аксиома 1.
Через любые три точки,
не лежащие на одной прямой, можно провести плоскость, и притом только одну.
A, B, C ∉ одной прямой | => (∃! α) A∈α, B∈α, C∈α
A, B, C ∉ одной прямой | => (∃! α) A∈α, B∈α, C∈α
Аксиомы стереометрии.
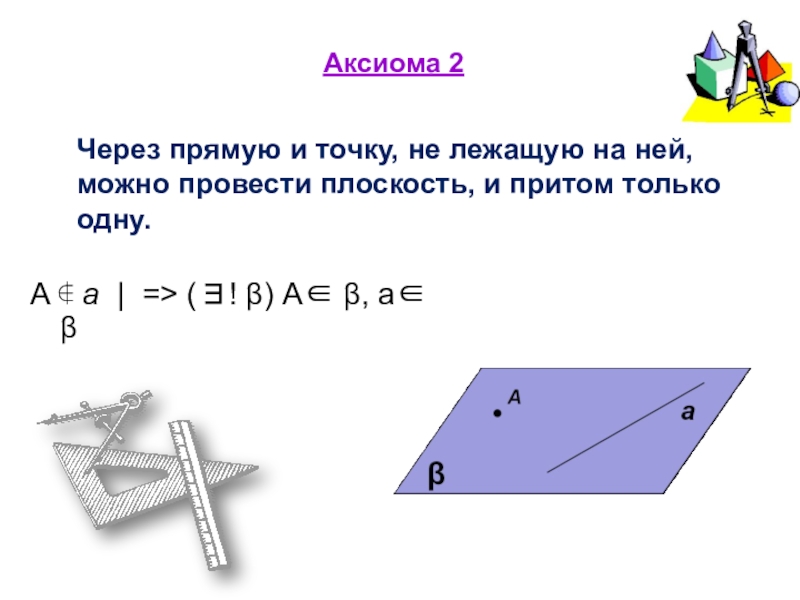
Слайд 10A ∉ a | => (∃! β) A∈ β, a∈ β
Аксиома 2
Через прямую и точку, не лежащую на ней, можно провести плоскость, и притом только одну.
Слайд 11Аксиома 3 Если две плоскости имеют общую точку, то они пересекаются по
прямой, проходящей через эту точку.
Слайд 12Способы задания плоскости:
1. Плоскость можно провести через три точки.
2. Можно провести
через прямую и не лежащую на ней точку.
Аксиома 1
Теорема 1
Теорема 2
3. Можно провести через две пересекающиеся прямые.
Слайд 13Взаимное расположение прямой и плоскости.
Прямая лежит в плоскости.
Прямая пересекает плоскость.
Прямая не
пересекает плоскость.
Множество общих точек.
Единственная общая точка.
Нет общих точек.
γ
а
γ
а
М
γ
а
Слайд 14Следствия из аксиом стереометрии.
Через прямую и не лежащую на ней точку
проходит плоскость, и притом только одна.
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Слайд 181.Пользуясь данным рисунком, назовите:
а) четыре точки, лежащие в плоскости SAB, в
плоскости АВС;
б) плоскость, в которой лежит прямая MN, прямая КМ;
в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.
б) плоскость, в которой лежит прямая MN, прямая КМ;
в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.
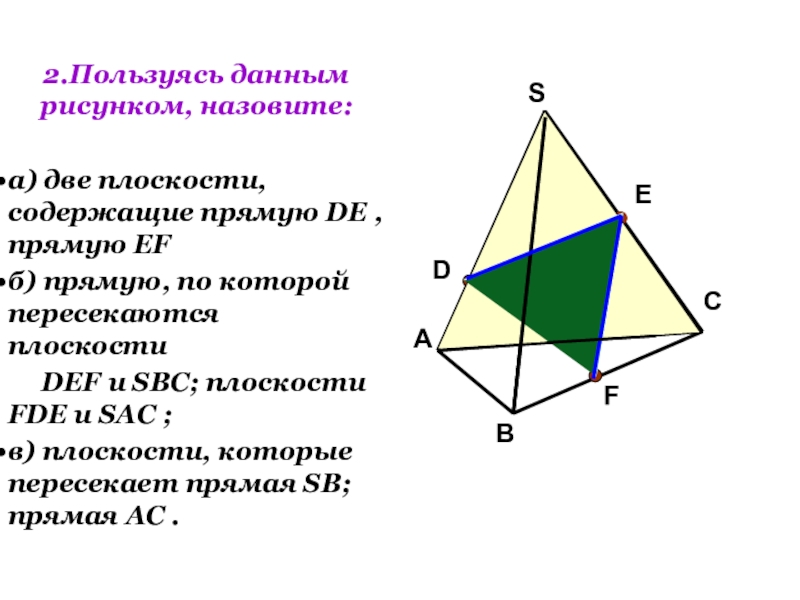
Слайд 192.Пользуясь данным рисунком, назовите:
а) две плоскости, содержащие прямую DE , прямую
EF
б) прямую, по которой пересекаются плоскости
DEF и SBC; плоскости FDE и SAC ;
в) плоскости, которые пересекает прямая SB; прямая AC .
б) прямую, по которой пересекаются плоскости
DEF и SBC; плоскости FDE и SAC ;
в) плоскости, которые пересекает прямая SB; прямая AC .
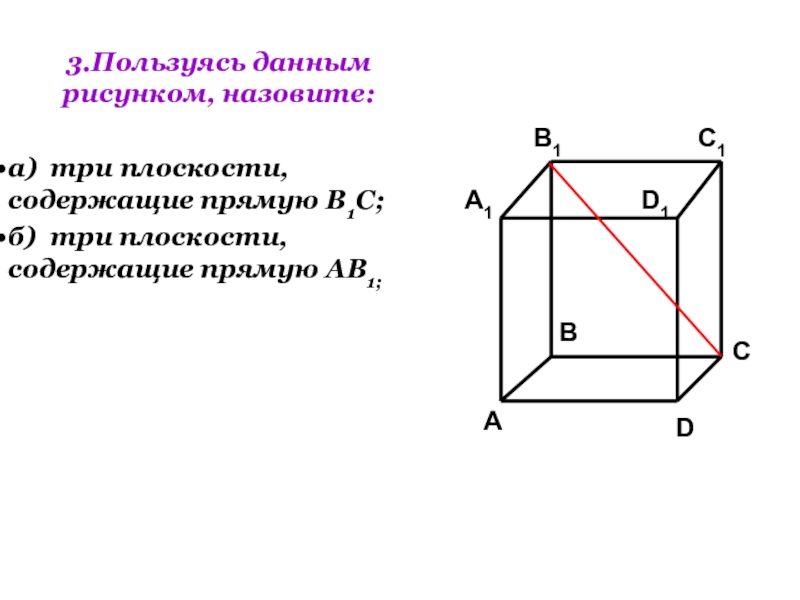
Слайд 203.Пользуясь данным рисунком, назовите:
а) три плоскости, содержащие прямую В1С;
б) три
плоскости, содержащие прямую АВ1;
Слайд 234.Пользуясь данным рисунком, назовите:
а) плоскость, не пересекающуюся с прямой CD1 ;
б) плоскость, не пересекающуюся с прямой BC1
