- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Отрицательные числа
Содержание
- 1. Презентация по теме: Отрицательные числа
- 2. Зачатки счета теряются в глубине веков, когда
- 3. Все началось в Китае во II в.
- 4. Китайский ученый Чжан Цань в книге «Арифметика
- 5. С ними производили вычисления и даже
- 6. Брахмагупта,астроном VII века, установил правила арифметических операций
- 7. В Европеотрицательные числа не признавали очень долго,
- 8. Ни египтяне, ни вавилоняне, ни древние
- 9. В Западной Европе отрицательные числа начинают
- 10. В 1544 году Михаил Штифель в книге
- 11. В 1685 году английский математик Джон Уоллис
- 12. Рене Декарттоже в XVII веке предложил откладывать
- 13. Гаусс, Уильман Гамильтон и Герман ГрассманВ 1831
- 14. Понадобилось несколько лет, чтобы идея Уоллиса получила
- 15. Числовая осьТока O разбивает прямую на два
- 16. КоординатыПрямую с выбранными на ней началом
- 17. Применение отрицательных чиселНапример, при указании численного значения
- 18. В географиивысота гор измеряется с помощью
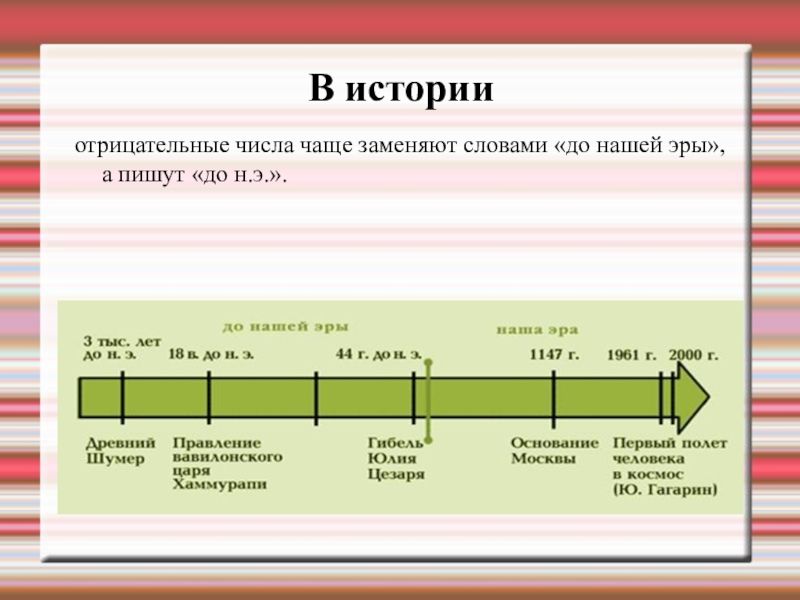
- 19. В историиотрицательные числа чаще заменяют словами «до нашей эры», а пишут «до н.э.».
- 20. «Сложение отрицательных чисел и чисел с
- 21. Правила сложения положительных и отрицательных
- 22. Правила умножения можно истолковать и таким
- 23. Презентация подготовлена по материалам интернета.Конец.Спасибо за внимание.
Слайд 1История появления отрицательных чисел
Работа
Муравлева Эльдара, ученика 6 класса
РЦДО
Руководитель
Ходина
2015 год
Слайд 2Зачатки счета теряются в глубине веков, когда ещё не было письменности.
История возникновения отрицательных чисел очень давняя и долгая. Они появились намного позже натуральных чисел и обыкновенных дробей. Решение уравнений и понятие «долга» при торговых расчетах привело к появлению отрицательных чисел.
Первые представления об отрицательных числах возникли еще до нашей эры, но люди долгое время не признавали их существования.
Слайд 3Все началось в Китае во II в. до н. э.
У
Китайцы размещали палочки на разграфленной доске так, чтобы каждое число занимало отдельную ячейку, а каждая колонка соответствовала одному уравнению. Решали уравнения, передвигая бамбуковые палочки. Если решение состояло из обычных палочек, это было истинное число, оно принималось. Если решение состояло из черных палочек, это было ложное число, и оно отбрасывалось.
Слайд 4Китайский ученый Чжан Цань в книге «Арифметика в девяти главах» приводит
Слайд 5С ними производили вычисления
и даже использовали в торговых расчетах.
Пример
Вы имеете
Результатом вычитания 4000 – 6000 является число 2000 со знаком «минус».
Это отрицательное число указывает на то, что у вас образовался долг 2000 рублей.
А в Индии
они использовались очень широко
Слайд 6Брахмагупта,
астроном VII века, установил правила арифметических операций с положительными
и отрицательными
Он описывал точное значение имущества и долга с помощью нуля и других девяти цифр, которые легли в основу десятичного представления чисел, используемого в настоящее время.
«Долг минус нуль ― это долг.
Имущество минус нуль ―
это имущество.
Нуль минус нуль ― это нуль.
Долг, вычтенный из нуля, ―
это имущество.
Имущество, вычтенное из нуля, ―
это долг.»
Слайд 7В Европе
отрицательные числа
не признавали очень долго,
их считали «мнимыми»
и
Слайд 8
Ни египтяне, ни вавилоняне, ни древние греки
отрицательных чисел не
Исключение составлял Диофант, который
в III веке н.э. рассматривал отрицательные числа
как «вычитаемые»,
а положительные
как «прибавляемые»
и уже умел умножать их и знал
правило знаков.
Слайд 9
В Западной Европе отрицательные числа
начинают использоваться только с XIII в.
Их описал Леонардо Пизанский (Фибоначчи)
в 1202 году в своем произведении
«Книга Абака».
При этом они обозначались словами
или сокращенными словами
как наименования
в именованных числах.
Слайд 10
В 1544 году Михаил Штифель в книге
«Полная арифметика» впервые ввел
«Нуль находится между абсурдными и истинными числами».
Слайд 11В 1685 году английский математик Джон Уоллис в своём труде
«Трактат
Он показал, что отрицательные числа нельзя считать
«ни бесполезными, ни абсурдными».
Числовая ось
«...если человек отойдет от ноля вперед на пять ярдов, а затем вернется назад на восемь ярдов, то он «переместится на позицию, которая на 3 ярда дальше, чем ничто. А значит, -3 ― это та же точка на линии, что и +3, но не вперед, как должно быть, а назад».
Слайд 12Рене Декарт
тоже в XVII веке предложил откладывать отрицательные числа на цифровой
многие ученые отрицали их.
Слайд 13Гаусс,
Уильман Гамильтон и Герман Грассман
В 1831 году Гаусс назвал отрицательные числа
абсолютно
А то, что не все действия с ними можно совершать, не считал чем -то страшным
(с дробями, например, тоже не все действия можно делать).
С этого времени отрицательные числа получили всеобщее признание
и современную форму обозначения.
Слайд 14Понадобилось несколько лет, чтобы идея Уоллиса получила широкое распространение, но теперь
Сейчас уже никто не сомневается в их реальности.
Мы принимаем отрицательные числа с числовой осью, а затем узнаем поразительную новость:
Минус, умноженный на минус, дает плюс. Вот это да!
Современное понимание отрицательных чисел
Слайд 15
Числовая ось
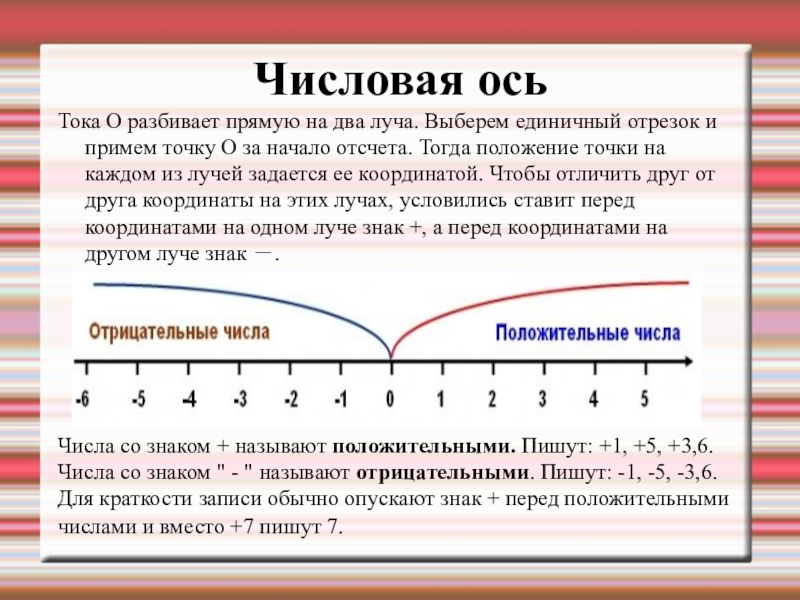
Тока O разбивает прямую на два луча. Выберем единичный отрезок
Числа со знаком + называют положительными. Пишут: +1, +5, +3,6. Числа со знаком " - " называют отрицательными. Пишут: -1, -5, -3,6.
Для краткости записи обычно опускают знак + перед положительными числами и вместо +7 пишут 7.
Слайд 16
Координаты
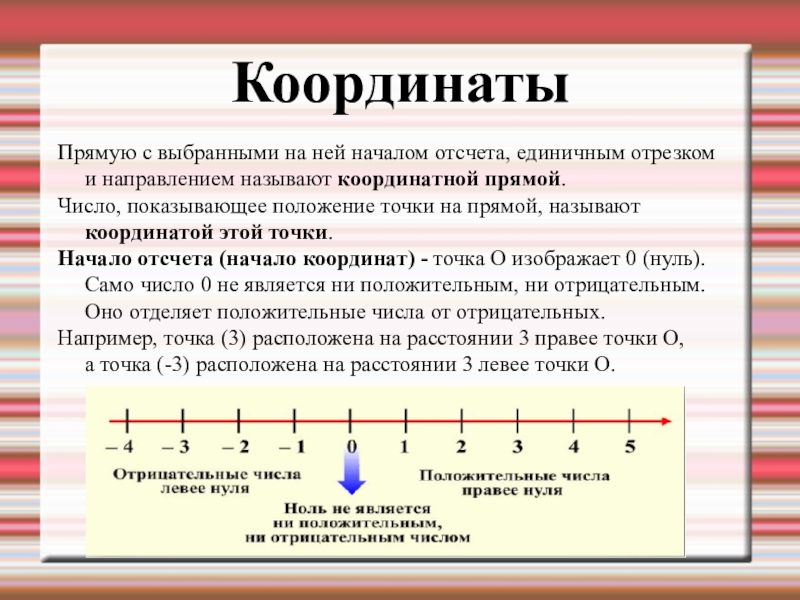
Прямую с выбранными на ней началом отсчета, единичным отрезком
и
Число, показывающее положение точки на прямой, называют координатой этой точки.
Начало отсчета (начало координат) - точка O изображает 0 (нуль). Само число 0 не является ни положительным, ни отрицательным. Оно отделяет положительные числа от отрицательных.
Например, точка (3) расположена на расстоянии 3 правее точки О, а точка (-3) расположена на расстоянии 3 левее точки О.
Слайд 17Применение отрицательных чисел
Например, при указании численного значения температуры приходится дополнительно пояснять:
Больше всего отрицательные числа встречаются в точных науках, в математике и физике.
У них множество разных областей применения,
кроме подсчета долгов, от графиков до термометров.
Слайд 18В географии
высота гор измеряется
с помощью положительных чисел (выше уровня моря),
Слайд 20«Сложение отрицательных чисел
и чисел с разными знаками»
Если уж захочется
Если числа с разными знаками дадут, Чтоб найти их сумму, все мы тут как тут. Больший модуль быстро очень выбираем. Из него мы меньший вычитаем. Самое же главное – знак не позабыть! - Вы какой поставите? – мы хотим спросить - Вам секрет откроем, проще дела нет, Знак, где модуль больше, запиши в ответ.
Слайд 21Правила сложения
положительных
и отрицательных чисел
Минус с минусом сложить,
Можно
Слайд 22Правила умножения
можно истолковать и таким образом:
«Друг моего друга - мой
«Враг моего врага - мой друг»: ─ ∙ ─ = +.
«Друг моего врага - мой враг»: + ∙ ─ = ─.
«Враг моего друга – мой враг»: ─ ∙ + = ─.
Или:
Знак умножения есть точка, в ней три знака:
_ + _ , + _ _ , + _+
Прикрой из них два, третий даст ответ. Например. Как определить знак произведения 2∙(-3)?
Закроем руками знаки «плюс» и «минус». Остаётся знак «минус»