- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Пропорция (6 класс)
Содержание
- 1. Презентация по математике Пропорция (6 класс)
- 2. Тема урока. ПРОПОРЦИИ. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ПРОПОРЦИИ.
- 3. Цели урока:Проверить умение находить неизвестный член пропорции.Отработать
- 4. Что такое пропорция? крайниеa:b=c:dсредние
- 5. Основное свойство пропорцииa*d=b*c
- 6. Найти неизвестный член пропорции х : 5
- 7. Из истории развития математики
- 8. BCAЗолотым сечением и даже «божественной пропорцией» называли
- 9. Знаменитый зодчий Ле Корбюзье нашел это отношение во многих пропорциях человеческой фигуры.
- 10. Золотое сечение чаще всего применяется в произведениях
- 11. Красивейшее произведение древнегреческой архитектуры – Парфенон –
- 12. Какие величины называются прямо пропорциональными? Что можно
- 13. Задача 2. Расфасовали 13,6 т
- 14. Какие величины называются обратно пропорциональными? Что можно
- 15. Задача 4. Теплоход «Ракета» прошел расстояние
- 16. Самостоятельная работа
- 17. ОТВЕТЫВариант №1 Вариант №2 Вариант №3
- 18. Домашнее задание№ 848 (1,2), № 823 (1).
Слайд 1УРОК МАТЕМАТИКИ В 6 КЛАССЕ подготовила учитель математики МБОУ «Гимназия №1» Рузаевского
Слайд 3Цели урока:
Проверить умение находить неизвестный член пропорции.
Отработать навыки решения задач с
Научить практическому применению знаний, полученных на уроке.
Слайд 6Найти неизвестный член пропорции
х : 5 = 24 : 4
3 : 4 = х : 20
5 : 8 = 20 : х
0,2 : 0,3 = 1,2 :х
х = 30
х = 2
х = 15
х = 32
х = 1,8
Слайд 8
B
C
A
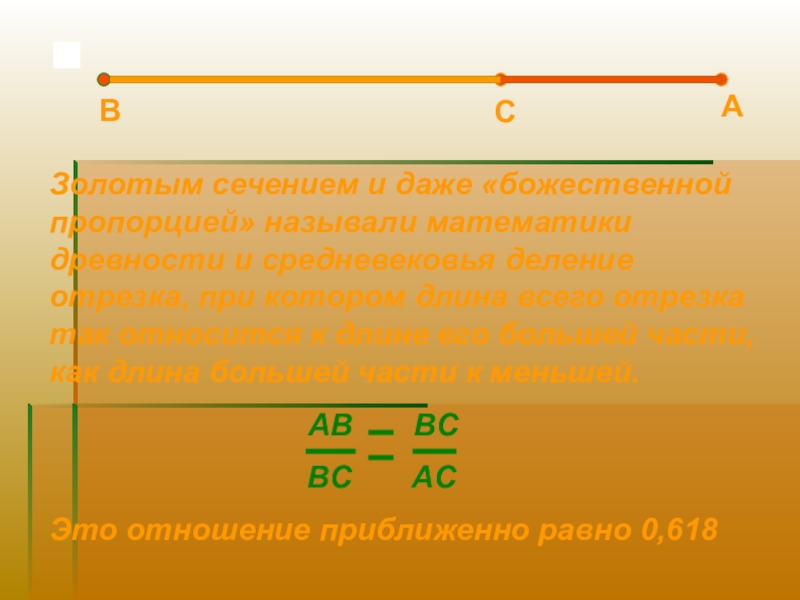
Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья
AB BC
BC AC
Это отношение приближенно равно 0,618
Слайд 10Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается в
Слайд 11Красивейшее произведение древнегреческой архитектуры – Парфенон – построено в V в.
Слайд 12Какие величины называются прямо пропорциональными?
Что можно сказать об отношениях этих величин?
Задача
При выпечке хлеба из килограмма ржаной муки пекарь получает 1,4 кг хлеба. Сколько килограммов муки расходуется на выпечку
21 ц хлеба?
1 кг муки – 1,4 кг хлеба
х кг муки – 2100 кг хлеба
Слайд 13 Задача 2.
Расфасовали 13,6 т зерна, что составляет 54%
13,6 т зерна – 54%
Х т зерна – 27%
54%
19%
?
Слайд 14Какие величины называются обратно пропорциональными? Что можно сказать об отношениях этих
Задача 3.
Пять каменщиков могут закончить работу за 9 дней. Инженер попросил ускорить работу и для этого добавил еще 10 каменщиков. За какое время они закончат работу, считая, что все каменщики будут работать с одинаковой производительностью?
5 кам. – 9 дней
15 кам. – х дней
Слайд 15 Задача 4.
Теплоход «Ракета» прошел расстояние между пристанями со скоростью
50 км/ч – 4,8 ч
Х км/ч – 3,2 ч
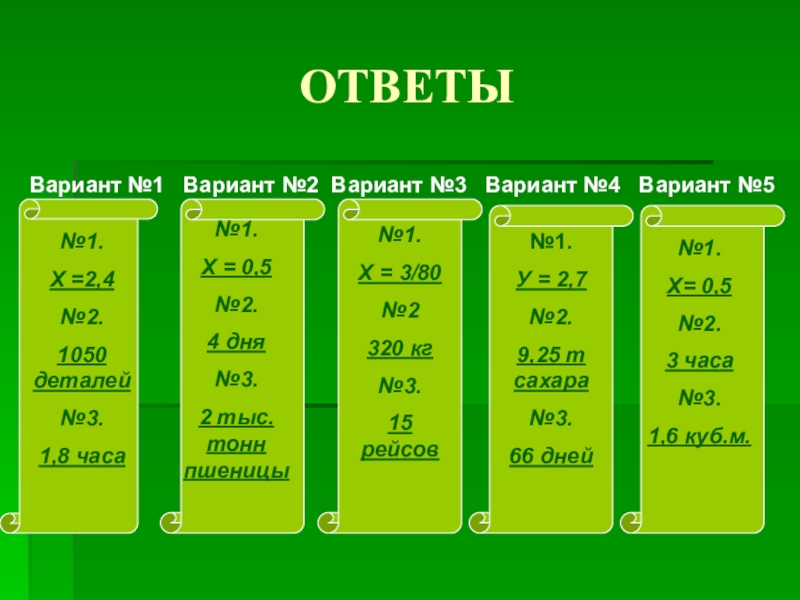
Слайд 17ОТВЕТЫ
Вариант №1 Вариант №2 Вариант №3 Вариант №4
№1.
Х= 0,5
№2.
3 часа
№3.
1,6 куб.м.
№1.
У = 2,7
№2.
9,25 т сахара
№3.
66 дней
№1.
Х = 3/80
№2
320 кг
№3.
15 рейсов
№1.
Х = 0,5
№2.
4 дня
№3.
2 тыс. тонн пшеницы
№1.
Х =2,4
№2.
1050 деталей
№3.
1,8 часа