- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Правильные многогранники
Содержание
- 1. Презентация по математике Правильные многогранники
- 2. Правильных многогранников вызывающе мало, но этот
- 3. сколько правильных многогранников существует?Пусть при одной вершине
- 4. Начиная с n=7 угол станет меньше 60о , а такого правильного n-угольника не существует.
- 5. Грани правильного многогранника – правильные треугольники, тогда
- 6. Грани правильного многогранника –квадраты, тогда
- 7. Грани правильного многогранника – правильные пятиугольники, тогда
- 8. Начиная с правильного шестиугольника
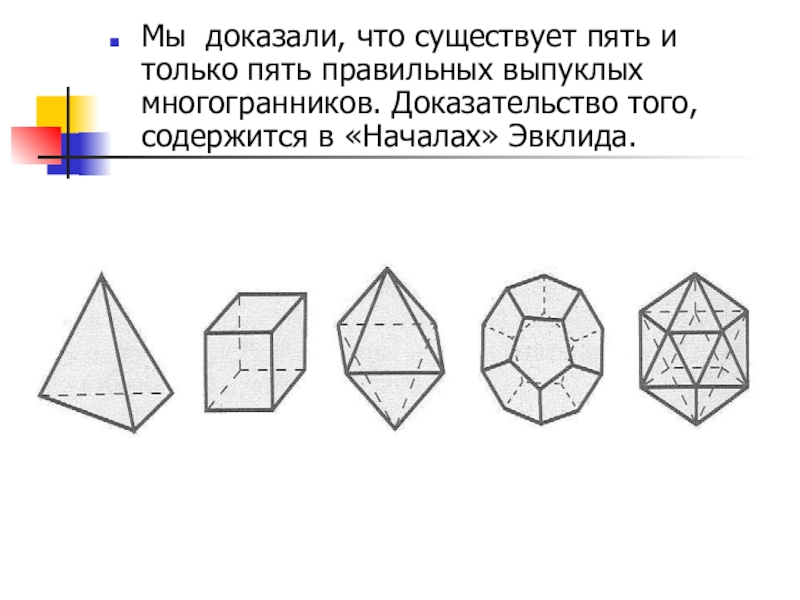
- 9. Мы доказали, что существует пять и только
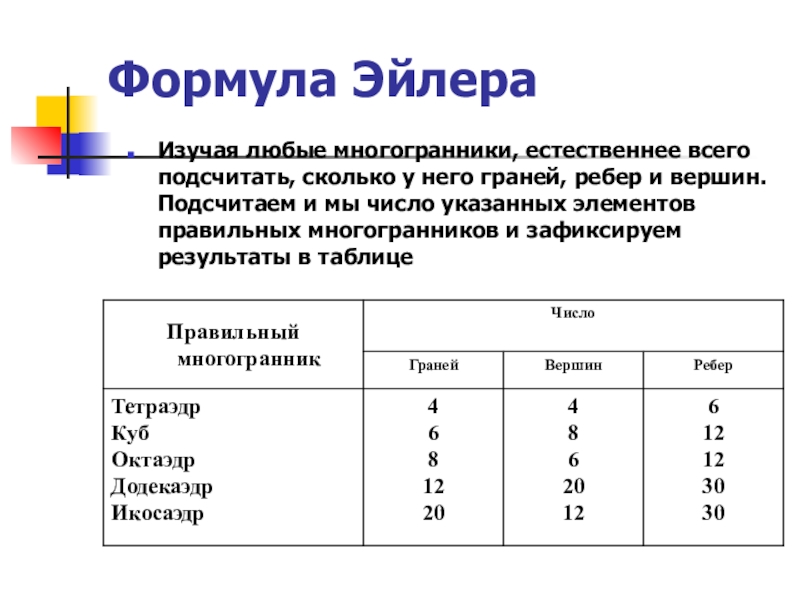
- 10. Формула Эйлера Изучая любые многогранники, естественнее всего
- 11. Сумма числа граней и вершин равна числу
- 12. Тетраэдр и его свойства Тетраэдр
- 13. Гексаэдр и его свойства Куб составлен из
- 14. Октаэдр.Октаэдр составлен из восьми равносторонних треугольников. Каждая
- 15. Икосаэдр Икосаэдр составлен из двадцати равносторонних треугольников.
- 16. Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая
- 17. Двойственность или сопряженность правильных многогранников.Если центры граней
- 18. вопросыКакое из перечисленных геометрических тел не является
- 19. Выберите верное утверждение:А)
- 20. 3.Найдите длину ребра куба, если длина его
- 21. А) правильный тетраэдр не имеет центра симметрии;Б)
- 22. Литература.1. Учебник. Л.С. Атанасян, В.Ф.
Слайд 1Правильные многогранники
Многогранник называется правильным, если:
он выпуклый,
в каждой вершине сходится одинаковое число граней,
все его двухгранные углы равны.
Слайд 2Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд
Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика.
Некоторые из правильных тел встречаются в природе в виде кристаллов,
другие – в виде вирусов (которые можно рассмотреть с помощью электронного микроскопа).
Пчелы строили шестиугольные соты задолго до появления человека,
а в истории цивилизации создание многогранных тел (подобных пирамидам) наряду с другими видами пластических искусств уходит в глубь веков.
Слайд 3сколько правильных многогранников существует?
Пусть при одной вершине сходится n – рёбер,
И все они равны между собой.
Пусть х – один из плоских углов, тогда сумма плоских углов при вершине – nx.
По свойству плоских углов nx<
Угол правильного n – угольника равен
360о
Слайд 5Грани правильного многогранника – правильные треугольники, тогда =
1. 60о * 3 = 180о < 360о , 4 грани - тетраэдр.
2. 60о * 4 = 240о < 360о , 8 граней – октаэдр.
3. 60о * 5 = 300о < 360о , 20 граней – икосаэдр.
60о * 6 = 360о
это противоречит теореме о сумме плоских углов многогранного угла,
значит больше правильных многогранников, грани которых – правильные треугольники не существует.
Слайд 6Грани правильного многогранника –квадраты, тогда
1. 90о * 3 = 270о < 360о - 6 граней – гексаэдр (куб).
2. 90о * 4 = 360о
значит больше правильных многогранников, грани которых
– квадраты не существует.
Слайд 7Грани правильного многогранника – правильные пятиугольники, тогда =
108о * 3 = 324о < 360о - 12граней –
додекаэдр.
108о * 4 > 360о
значит больше правильных многогранников, грани которых –
правильные пятиугольники не существует.
Слайд 8Начиная с правильного шестиугольника >120о
Cледовательно n* >360о (n>3),
Поэтому правильных многогранников,
грани которых – правильные многоугольники с числом сторон больше 5 ,
не существует!
о
Слайд 9
Мы доказали, что существует пять и только пять правильных выпуклых многогранников.
Слайд 10Формула Эйлера
Изучая любые многогранники, естественнее всего подсчитать, сколько у него
Слайд 11Сумма числа граней и вершин равна числу ребер, увеличенному на 2:
Эта формула была подмечена уже Декартом в 1640 году, а позднее переоткрыта Эйлером (1752), имя которого с тех пор она и носит. Формула Эйлера верна для любых выпуклых многогранников.
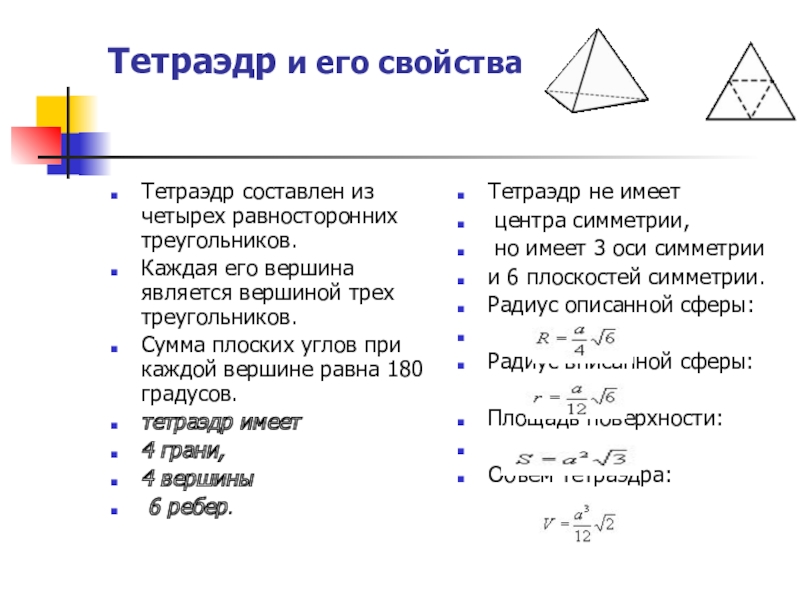
Слайд 12Тетраэдр и его свойства
Тетраэдр составлен из четырех равносторонних треугольников.
Каждая
Сумма плоских углов при каждой вершине равна 180 градусов.
тетраэдр имеет
4 грани,
4 вершины
6 ребер.
Тетраэдр не имеет
центра симметрии,
но имеет 3 оси симметрии
и 6 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем тетраэдра:
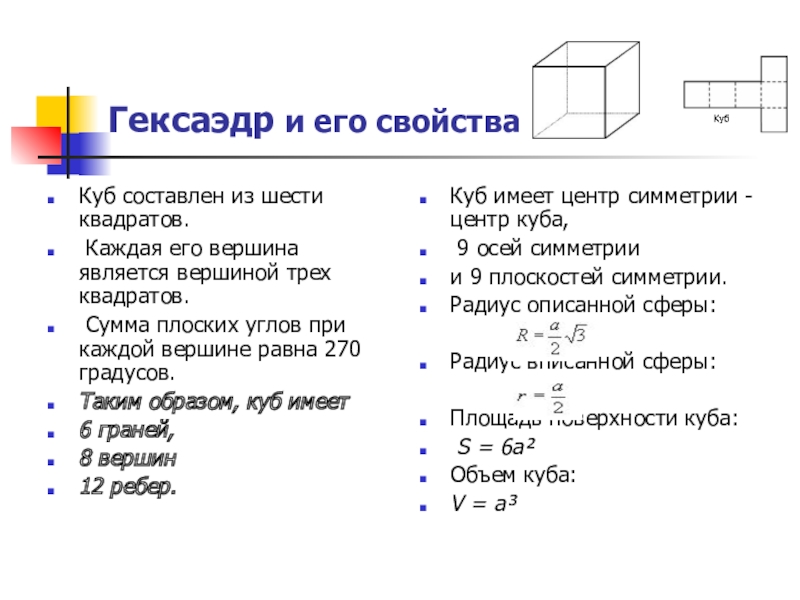
Слайд 13Гексаэдр и его свойства
Куб составлен из шести квадратов.
Каждая его
Сумма плоских углов при каждой вершине равна 270 градусов.
Таким образом, куб имеет
6 граней,
8 вершин
12 ребер.
Куб имеет центр симметрии - центр куба,
9 осей симметрии
и 9 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности куба:
S = 6a²
Объем куба:
V = a³
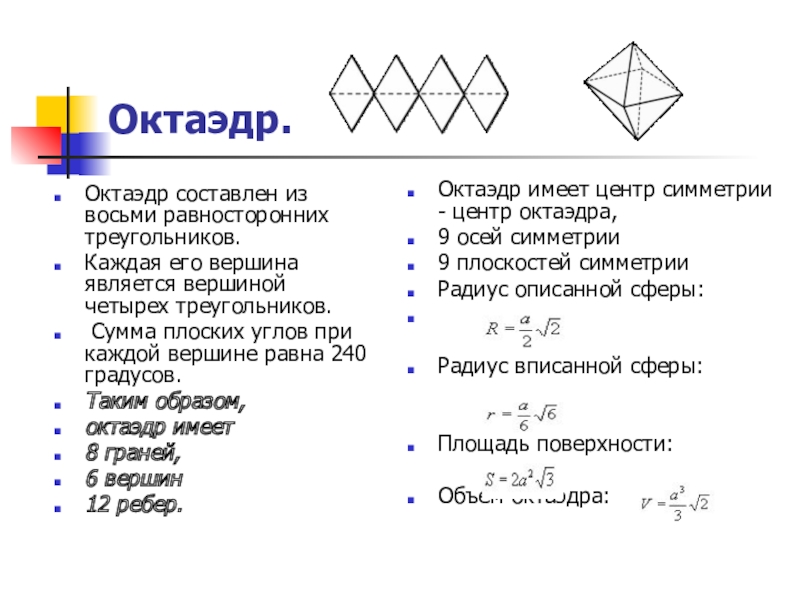
Слайд 14Октаэдр.
Октаэдр составлен из восьми равносторонних треугольников.
Каждая его вершина является вершиной
Сумма плоских углов при каждой вершине равна 240 градусов.
Таким образом,
октаэдр имеет
8 граней,
6 вершин
12 ребер.
Октаэдр имеет центр симметрии - центр октаэдра,
9 осей симметрии
9 плоскостей симметрии
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем октаэдра:
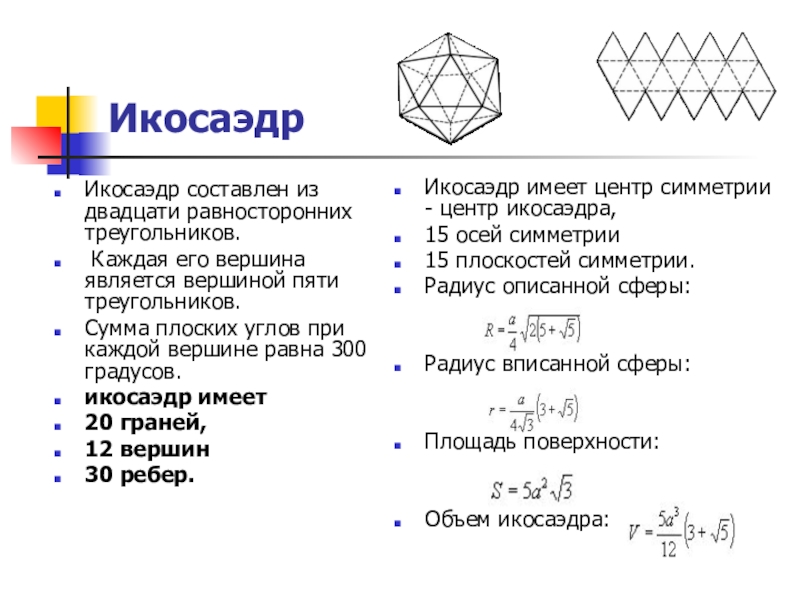
Слайд 15Икосаэдр
Икосаэдр составлен из двадцати равносторонних треугольников.
Каждая его вершина является
Сумма плоских углов при каждой вершине равна 300 градусов.
икосаэдр имеет
20 граней,
12 вершин
30 ребер.
Икосаэдр имеет центр симметрии - центр икосаэдра,
15 осей симметрии
15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем икосаэдра:
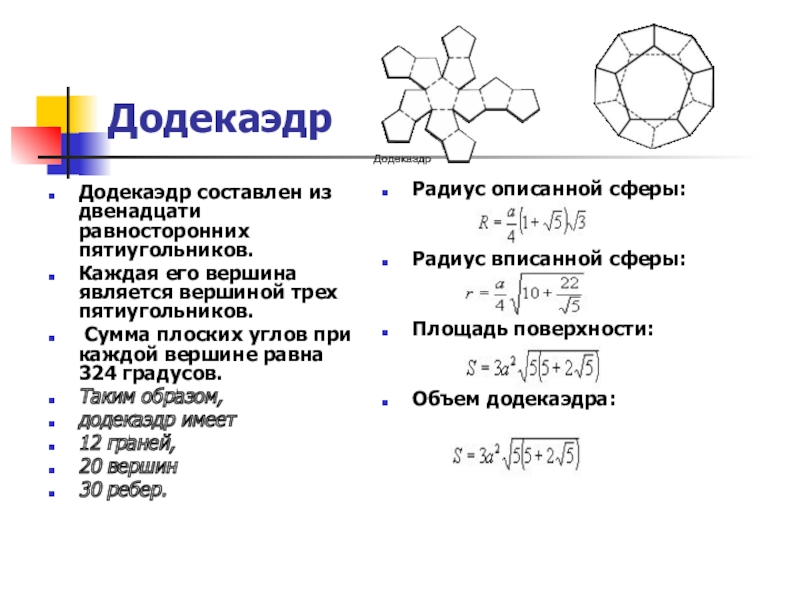
Слайд 16Додекаэдр составлен из двенадцати равносторонних пятиугольников.
Каждая его вершина является вершиной
Сумма плоских углов при каждой вершине равна 324 градусов.
Таким образом,
додекаэдр имеет
12 граней,
20 вершин
30 ребер.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем додекаэдра:
Додекаэдр
Слайд 17Двойственность или сопряженность правильных многогранников.
Если центры граней куба соединить отрезками, то
То есть вписанный в куб октаэдр.
Обратно: центры граней октаэдра являются вершинами вписанного куба.
Двойственными являются икосаэдр и додекаэдр.
Тетраэдр двойственен сам себе.
Слайд 18вопросы
Какое из перечисленных геометрических тел не является правильным многогранником:
А) правильный тетраэдр;
Б)
В) правильная призма;
Г) правильный додекаэдр;
Д) правильный октаэдр
Ответ: в
Слайд 19
Выберите верное утверждение:
А) выпуклый многогранник называется правильным, если его грани
Б) правильная треугольная пирамида и правильный тетраэдр – это одно и то же;
В) из всех правильных многогранников только правильный тетраэдр имеет центр симметрии;
Г) не существует правильного многогранника, гранями которого являются правильные шестиугольники;
Д) правильный тетраэдр состоит из 8 правильных треугольников.
Ответ: Г
Слайд 20
3.Найдите длину ребра куба, если длина его диагонали равна 15 см.
Ответ: (5 )
4. Найдите площадь полной поверхности правильного октаэдра, если его ребро равно 6 см.
Ответ: 72
Слайд 21А) правильный тетраэдр не имеет центра симметрии;
Б) центры граней правильного октаэдра
В) центры граней куба являются вершинами правильного тетраэдра;
Г) правильный додекаэдр состоит из 12 правильных пятиугольников;
Д) сумма плоских углов при каждой вершине куба равна 270.
ответ: В
5. Какое из следующих утверждений неверно:
Слайд 22
Литература.
1. Учебник. Л.С. Атанасян, В.Ф. Бутузов, и др. Геометрия, 10-11
2. Пособие для поступающих в вузы .Кутасов А.Д., Пиголкина Т.С. и др.. М., «Наука», 1985.
3.Информатика: Лабораторный практикум. Создание текстовых документов в текстовом редакторе Microsoft Word 2000/ Авт.-сост. В.Н. Голубцов, А.К.Козырев и др., Саратов: Лицей, 2003.
4.Сборник конкурсных задач по математике для поступающих в вузы под ред. Сканави М.И., Санкт-Петербург, 1994.
5. Интернет – сайты.
7. Курант Р., Роббинс Г. Что такое математика? М., 1967.
8. Кованцов Н.И. Математика и романтика. Киев, 1976.
9. Кокстер Г.С.М. Введение в геометрию. М., 1966.
10. Смирнова И.М. В мире многогранников. М., 1990.
11. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. М., 1992.
12. Энциклопедический словарь юного математика. М., 1989.