- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Последовательность Фибоначчи (6 класс)
Содержание
- 1. Презентация по математике Последовательность Фибоначчи (6 класс)
- 2. Ребята, что такое последовательность?Последовательность – одно из
- 3. Последовательность Фибоначчи описана итальянским математиком 13 века.
- 4. Последовательность Фибоначчи начинается с двух единиц, каждое
- 5. 5+8=13 1,1,2,3,5,8,13Ребята, составьте сами еще
- 6. Ребята, давайте поделим число из последовательности на
- 7. Частное от деления любого числа последовательности на
- 8. Рассмотрим цветок подсолнечника (или просто подсолнух)
- 9. Ребята, что мы видим?Семена расположены по спиралям
- 10. В структуре цветка появились два идущих друг
- 11. Еще примерыКоличество лепестков многих цветов - это
- 12. Еще примеры
- 13. Еще примерыВ 1968г. Американский математик Альфред Броссо
- 14. Задача про кроликовСколько пар кроликов будет у
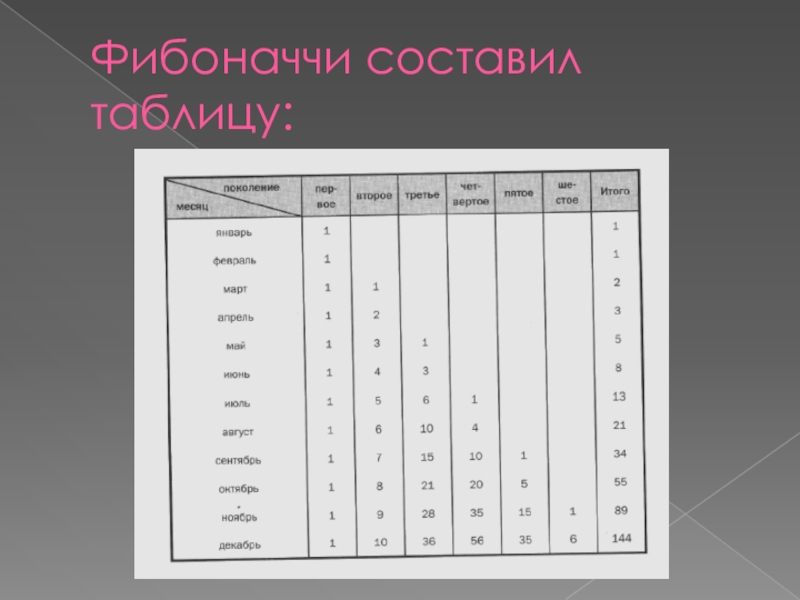
- 15. Фибоначчи составил таблицу:
- 16. ИтогиРебята, давайте вспомним:По какому закону составлена последовательность
Ребята, что такое последовательность?Последовательность – одно из основных понятий математики. Сегодня нас интересует, прежде всего числовая последовательность.Числовая последовательность состоит из чисел, каждое из которых получено по определенному закону. Каждое число последовательности называется членом последовательности и имеет
Слайд 1Презентация «Последовательность Фибоначчи»
Регнер Сергей Александрович
Учитель математики
МОУ СОШ № 13 г.Копейска
Слайд 2Ребята, что такое последовательность?
Последовательность – одно из основных понятий математики.
Сегодня
нас интересует, прежде всего числовая последовательность.
Числовая последовательность состоит из чисел, каждое из которых получено по определенному закону.
Каждое число последовательности называется членом последовательности и имеет свой номер (т.е. стоит на первом месте, значит номер один, на втором месте – номер два и т.д.)
Числовая последовательность состоит из чисел, каждое из которых получено по определенному закону.
Каждое число последовательности называется членом последовательности и имеет свой номер (т.е. стоит на первом месте, значит номер один, на втором месте – номер два и т.д.)
Слайд 3Последовательность Фибоначчи описана итальянским математиком 13 века.
Леона́рдо Пиза́нский (около 1170
года - около 1250 года) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи.
Слайд 4Последовательность Фибоначчи начинается с двух единиц, каждое следующее число равно сумме
двух предыдущих.
Вот она: 1,1,
1+1=2 1,1,2
2+1=3 1,1,2,3
3+2=5 1,1,2,3,5
5+3=8 1,1,2,3,5,8
Вот она: 1,1,
1+1=2 1,1,2
2+1=3 1,1,2,3
3+2=5 1,1,2,3,5
5+3=8 1,1,2,3,5,8
Слайд 55+8=13 1,1,2,3,5,8,13
Ребята, составьте сами еще 4 члена этой последовательности,
что мы получим?
1,1,2,3,5,8,13,21,34,55,89,…
Оказывается эта последовательность связана с золотым сечением и числом Фи.
1,1,2,3,5,8,13,21,34,55,89,…
Оказывается эта последовательность связана с золотым сечением и числом Фи.
Слайд 6Ребята, давайте поделим число из последовательности на предыдущее число, т.е.
второй
член на первый,
потом третий на второй,
Затем четвертый на третий….
Что мы получим?
потом третий на второй,
Затем четвертый на третий….
Что мы получим?
Слайд 7Частное от деления любого числа последовательности на предшествующее ему число будет
стремиться к числу Фи.
Для сорокового числа последовательности частное совпадет с «золотым» числом с точностью до четырнадцатого знака после запятой.
Связи между золотым сечением и числами Фибоначчи многочисленны и неожиданные.
Для сорокового числа последовательности частное совпадет с «золотым» числом с точностью до четырнадцатого знака после запятой.
Связи между золотым сечением и числами Фибоначчи многочисленны и неожиданные.
Слайд 9Ребята, что мы видим?
Семена расположены по спиралям двух видов: по часовой
и против часовой стрелки. Если мы посчитаем спирали по часовой стрелке и против, то получим два числа 21 и 34. Где мы уже встречали эти числа?
Слайд 10В структуре цветка появились два идущих друг за другом числа из
последовательности Фибоначчи.
Если мы проведем такой эксперимент с другим цветком мы получим другую пару чисел, например, 55 и 89.
Если мы проведем такой эксперимент с другим цветком мы получим другую пару чисел, например, 55 и 89.
Слайд 11Еще примеры
Количество лепестков многих цветов - это числа из последовательности Фибоначчи:
Например,
у сирени – 3 лепестка
Лютик- 5
Шиповник-8
Календула -15
Ромашка -21или 34, 55, 89.
Лютик- 5
Шиповник-8
Календула -15
Ромашка -21или 34, 55, 89.
Слайд 13Еще примеры
В 1968г. Американский математик Альфред Броссо изучил 4290 шишек десяти
различных видов и доказал, что с незначительным исключением, проявляется последовательность Фибоначчи.
Слайд 14Задача про кроликов
Сколько пар кроликов будет у нас через год, если
в январе у нас была одна пара, которая каждый месяц производит на свет другую пара. Начиная с марта пара, в свою очередь, производит собственное потомство каждый месяц, начиная со второго месяца.
Слайд 16Итоги
Ребята, давайте вспомним:
По какому закону составлена последовательность Фибоначчи?
Как она связана с
числом Фи?
Где в природе мы встречаем числа из последовательность Фибоначчи?
Где в природе мы встречаем числа из последовательность Фибоначчи?