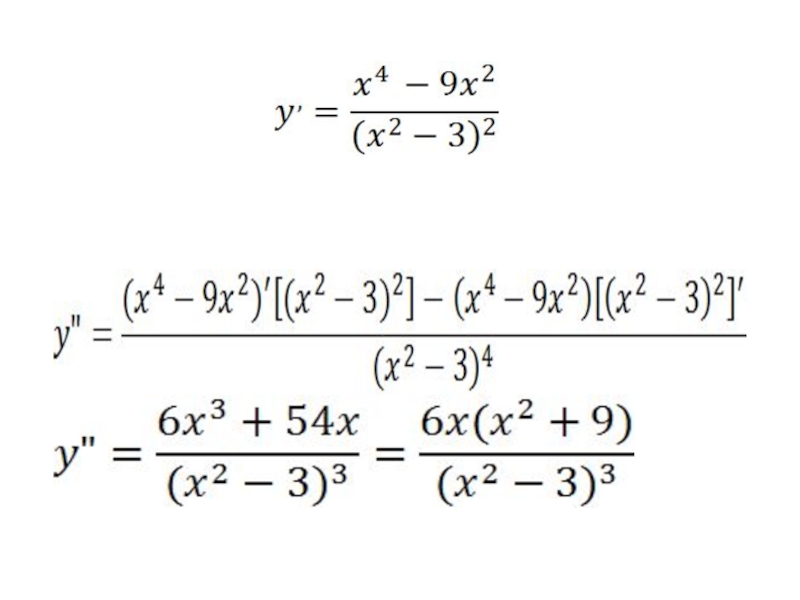- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Полное исследование и построение графика функции
Содержание
- 1. Презентация по математике Полное исследование и построение графика функции
- 2. Исследовать и построить график функции:
- 3. 1. Область определения функции. Найдем D(y) Функция существует при График имеет три ветви.
- 4. 2. Четность функции. Выясним является функция четной,
- 5. Получили, что
- 6. 3. Точки пересечения графика функции с осями
- 7. 4.Промежутки знакапостоянстваНайдем корни числителя и знаменателя, нанесем их на числовую ось и расставим знаки:
- 8. 5.Промежутки монотонности функции и ее экстремумы.
- 9. Приравняем производную к нулю:x=0 x=3 x=-3
- 10. Определим критические точки, для чего знаменатель приравняем
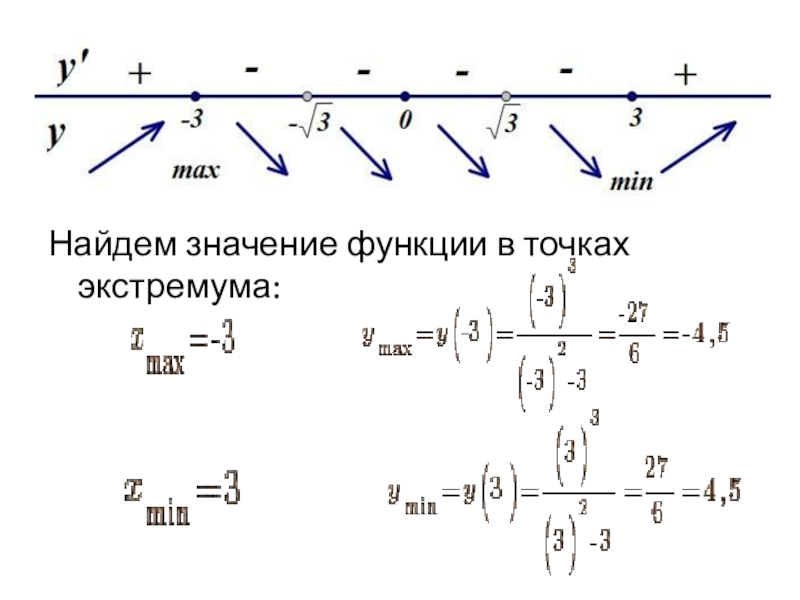
- 11. Найдем значение функции в точках экстремума:
- 12. 6.Выпуклость, вогнутость и точки перегиба функции. Для
- 13. Слайд 13
- 14. Определяем критические и стационарные точки. Критическими
- 15. Слайд 15
- 16. 7. Асимптоты функцииВертикальные асимптоты это прямые Уравнение горизонтальной
- 17. Найдем наклонную асимптоту. Уравнение наклонной асимптоты
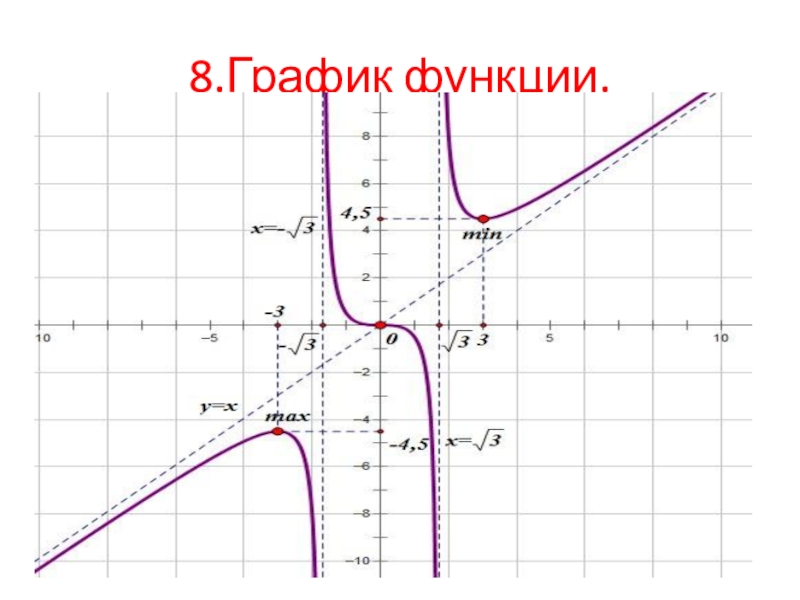
- 18. 8.График функции.
- 19. 9.Анализ графика функции.После построения графика необходимо еще
Исследовать и построить график функции:
Слайд 42. Четность функции.
Выясним является функция четной, нечетной или общего вида.
Область
определения функции симметрична относительна нуля (мы выкололи две симметричные точки)
Слайд 5Получили, что
следовательно,
функция нечетная, и график функции симметричен относительно начала координат.
функция нечетная, и график функции симметричен относительно начала координат.
Слайд 63. Точки пересечения графика функции с осями координат
а) Точки пересечения с
осью ОХ (y=0)
x=0
б) Точки пересечения с осью ОY (x=0)
График нашей функции проходит через начало координат.
x=0
б) Точки пересечения с осью ОY (x=0)
График нашей функции проходит через начало координат.
Слайд 74.Промежутки знакапостоянства
Найдем корни числителя и знаменателя, нанесем их на числовую ось
и расставим знаки:
Слайд 85.Промежутки монотонности функции и ее экстремумы.
Находим интервалы возрастания и убывания
функции и ее экстремумы, для чего находим первую производную функции :
Для определения производной дроби используем формулу:
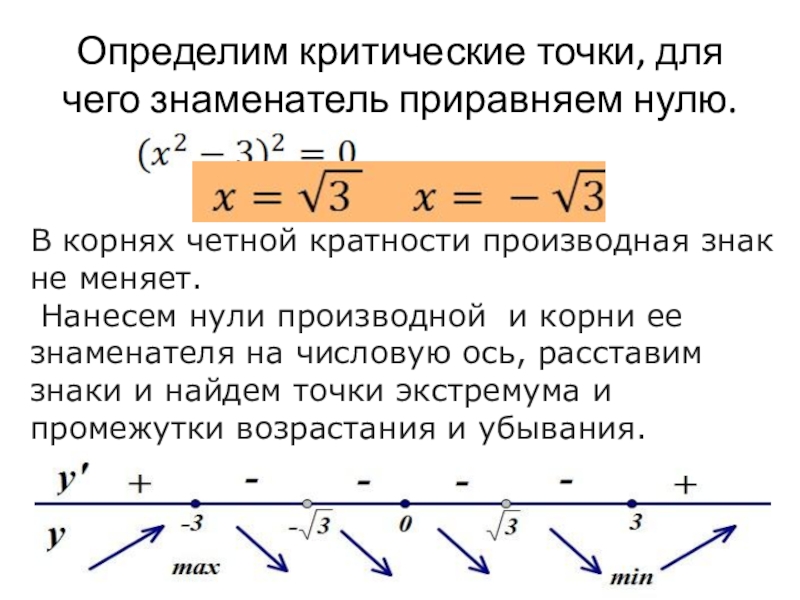
Слайд 10Определим критические точки, для чего знаменатель приравняем нулю.
В корнях четной кратности
производная знак не меняет.
Нанесем нули производной и корни ее знаменателя на числовую ось, расставим знаки и найдем точки экстремума и промежутки возрастания и убывания.
Нанесем нули производной и корни ее знаменателя на числовую ось, расставим знаки и найдем точки экстремума и промежутки возрастания и убывания.
Слайд 126.Выпуклость, вогнутость и точки перегиба функции.
Для определения выпуклости и вогнутости необходимо
найти вторую производную заданной функции
или первую производную функции
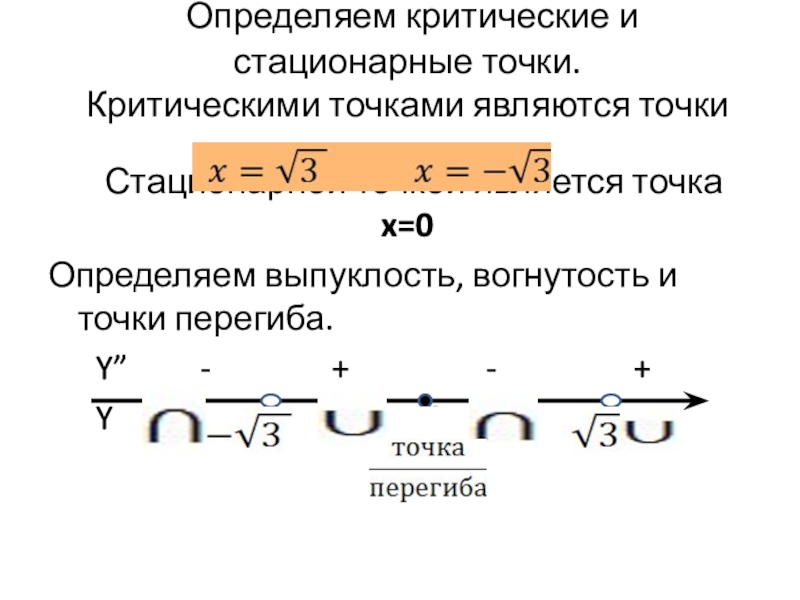
Слайд 14 Определяем критические и стационарные точки. Критическими точками являются точки Стационарной точкой
является точка x=0
Определяем выпуклость, вогнутость и точки перегиба.
Y” - + - +
Y 0
Слайд 15 Функция вогнута на интервале
( ; 0) ( )
Функция выпукла на интервале
(-∞; ) (0; )
Точка перегиба x=0
Слайд 167. Асимптоты функции
Вертикальные асимптоты это прямые
Уравнение горизонтальной асимптоты функции имеет вид
y=b, где
Степень числителя дроби на единицу больше степени знаменателя, поэтому предел не существует, и график функции не имеет горизонтальной асимптоты.
Степень числителя дроби на единицу больше степени знаменателя, поэтому предел не существует, и график функции не имеет горизонтальной асимптоты.
Слайд 17 Найдем наклонную асимптоту. Уравнение наклонной асимптоты имеет вид y=kx+b
.
Коэффициенты k и b вычисляются следующим образом:
Уравнение наклонной асимптоты имеет вид
.
Слайд 199.Анализ графика функции.
После построения графика необходимо еще раз просмотреть все пункты
исследования функции и проверить, соответствует ли полученный график всем пунктам.
Если наблюдается какое-то несоответствие, то необходимо повторить исследование и найти причину нестыковки графика и поведения функции.
Если наблюдается какое-то несоответствие, то необходимо повторить исследование и найти причину нестыковки графика и поведения функции.