живём в век, когда ещё можно делать открытия".
американский учёный, физик Р.Фейман
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Скалярное произведение векторов
Содержание
- 1. Презентация по математике на тему Скалярное произведение векторов
- 2. Цели урока:Ввести понятия угла между векторами
- 3. Оцените Ваше настроение
- 4. Повторение:Какие векторы называются равными?Как найти длину вектора по координатам его начала и конца?АВКакие векторы называются коллинеарными?или
- 5. Повторение:(Векторы в пространстве)1) Дано: Найти:2) Дано: Равны
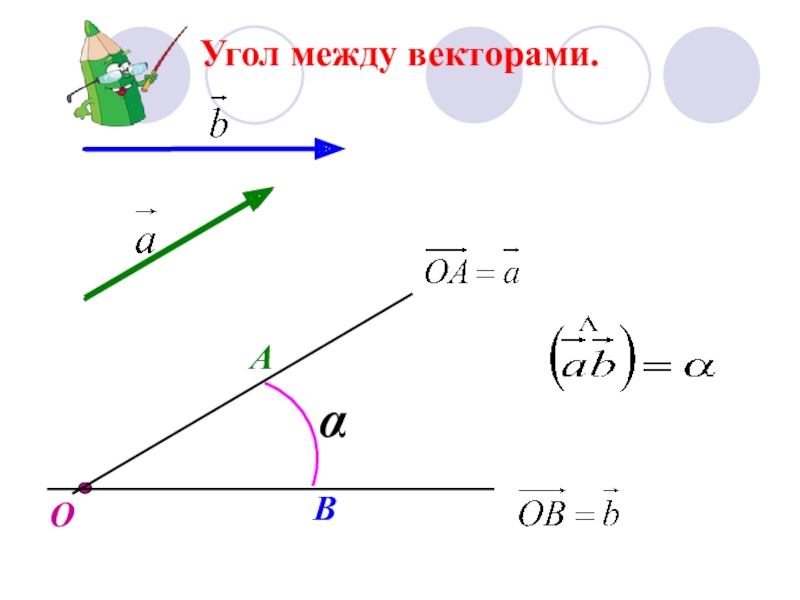
- 6. Угол между векторами.ОАВα
- 7. Скалярное произведение векторов.Скалярным произведением двух векторов называетсяпроизведение их длинна косинус угла междуними.Скалярное произведение векторов – число!
- 8. Примеры: ,
- 9. 1. Если
- 10. Скаляр – лат. scale – шкала.Ввёл в 1845 г.У. ГАМИЛЬТОН, английский математик.
- 11. Формула скалярного произведения векторов в пространстве.Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
- 12. Вычислить скалярное произведение векторова = (4; –6;
- 13. Упражнение для глаз
- 14. Формула для вычисления угла между векторами, заданными своими координатами
- 15. Формула для вычисления угла между векторами, заданными своими координатамиcos α = a • ba • b
- 16. Решение задач1.Найти угол между векторами а =
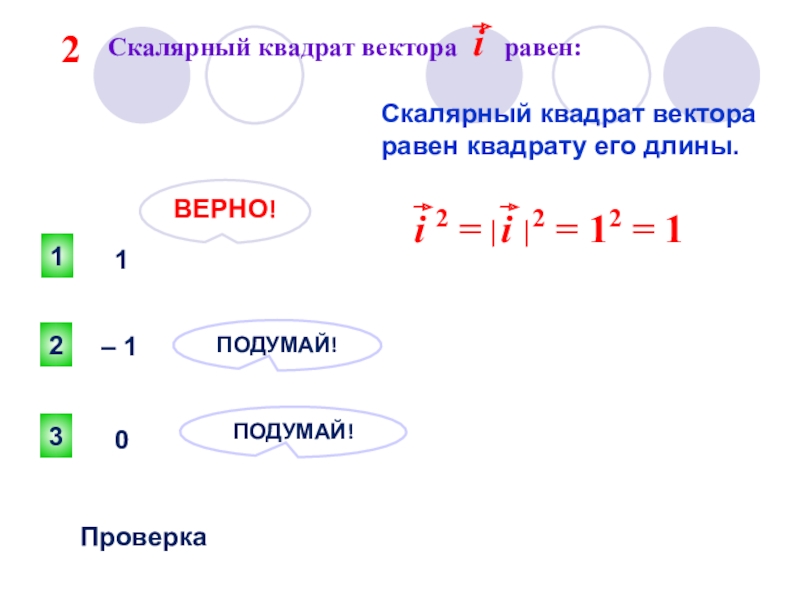
- 17. Скалярное произведение координатных
- 18. 1ВЕРНО!23ПОДУМАЙ!ПОДУМАЙ!Проверка1– 10Скалярный квадрат вектора равен квадрату его длины. 2
- 19. 1ВЕРНО!23ПОДУМАЙ!Проверкато векторы и : сонаправлены;противоположно направлены.перпендикулярны;34ПОДУМАЙ!123
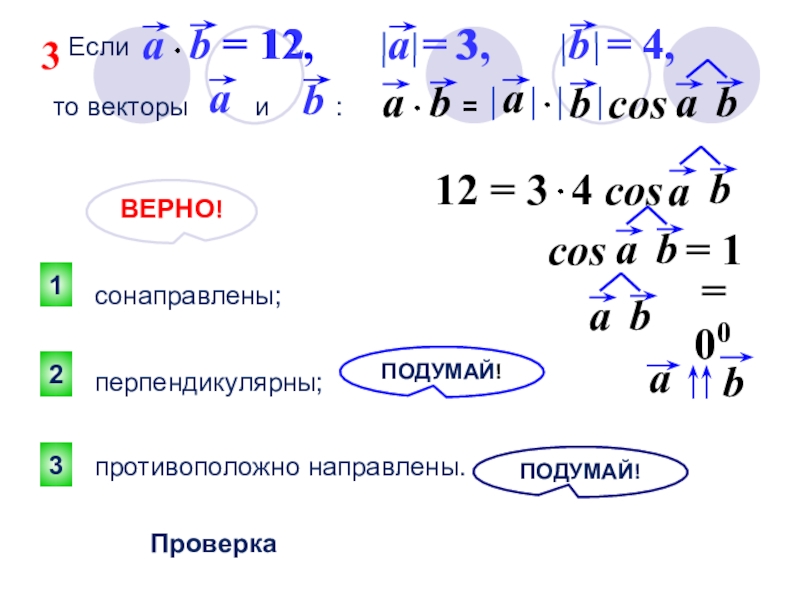
- 20. ПОДУМАЙ!321ПОДУМАЙ!ПроверкаЕсли= –20,x = 4, y = 5,то
- 21. 3ВЕРНО!21ПОДУМАЙ!ПОДУМАЙ!Проверка5006001200Найдите угол между векторами
- 22. «Синквейн» - французское слово, обозначающее «пять
- 23. С и н к в е й нУголОстрый, прямойСоставляется, строится, вычисляется Связан со скалярным произведениемВектор
- 24. Домашнее заданиеВыучить формулы скалярного произведения векторов и нахождения угла между ними;Подготовить кроссворд по теме «Векторы»
- 25. Оцените Ваше настроение
- 26. Спасибо за урок!
Цели урока:Ввести понятия угла между векторами и скалярного произведения векторов.Рассмотреть формулу скалярного произведения в координатах.Показать применение скалярного произведения векторов при решении задач.
Слайд 2Цели урока:
Ввести понятия угла между
векторами и скалярного
произведения векторов.
Рассмотреть формулу
скалярного произведения в координатах.
Показать применение скалярного произведения векторов при решении задач.
Рассмотреть формулу
скалярного произведения в координатах.
Показать применение скалярного произведения векторов при решении задач.
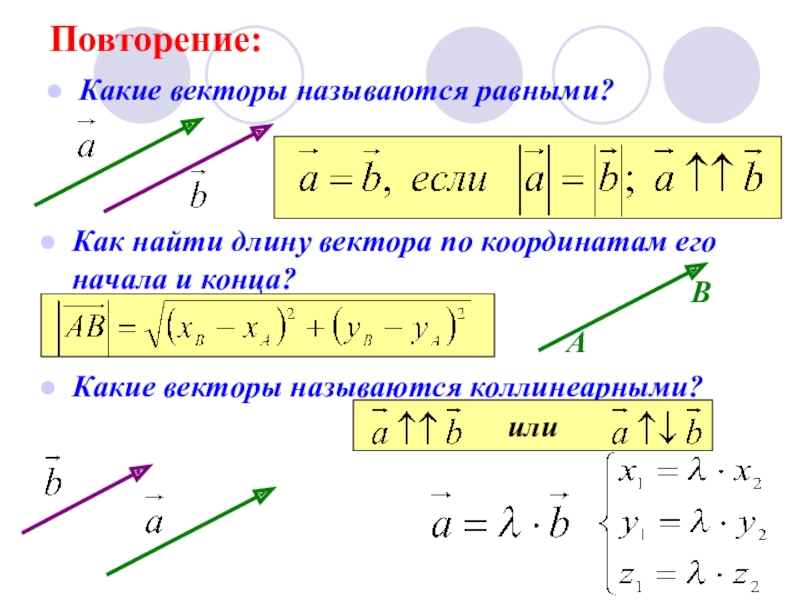
Слайд 4Повторение:
Какие векторы называются равными?
Как найти длину вектора по координатам его начала
и конца?
А
В
Какие векторы называются коллинеарными?
или
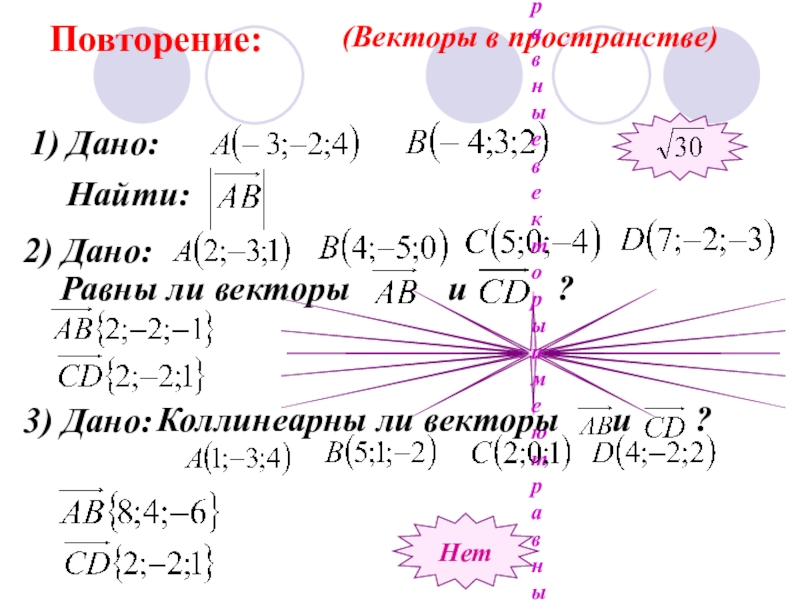
Слайд 5Повторение:
(Векторы в пространстве)
1) Дано:
Найти:
2) Дано:
Равны ли векторы
и ?
Нет, т.к.равные векторы имеют равные
координаты.
3) Дано:
Коллинеарны ли векторы и ?
Нет
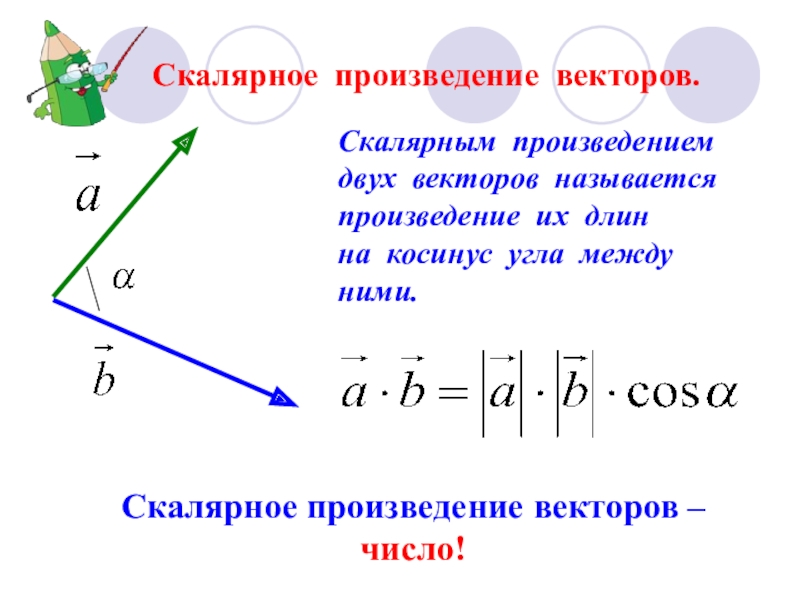
Слайд 7Скалярное произведение векторов.
Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла
между
ними.
ними.
Скалярное произведение векторов – число!
Слайд 9
1. Если , то
2.
Если
, то
3. Если
, то
4. Если
, то
Скалярное произведение
называется
скалярным квадратом вектора
Свойства скалярного произведения
Слайд 11Формула скалярного произведения векторов в пространстве.
Скалярное произведение двух векторов равно сумме
произведений соответствующих координат этих векторов.
Слайд 12Вычислить скалярное произведение векторов
а = (4; –6; 3), b = (–5;
2; –5), c = (0; –3; –4).
а = (4; –6; 3), b = (–5; 2; –5), c = (0; –3; –4).
a•b =
a•c =
b•c =
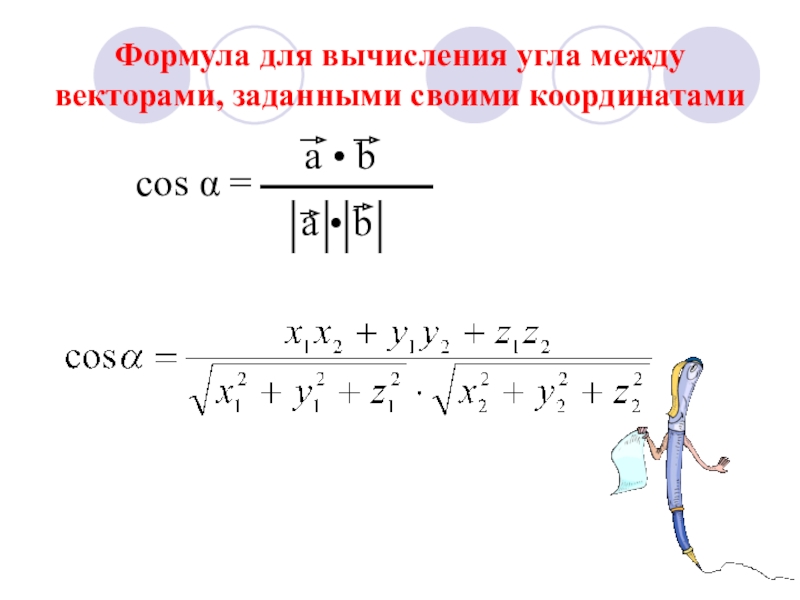
Слайд 15Формула для вычисления угла между векторами, заданными своими координатами
cos α =
a • b
a • b
Слайд 16Решение задач
1.Найти угол между векторами а = (1; -2), b =
(-3; 1).
2. В треугольнике АВС найти величину угла В, если А (0; 5; 0), В (4; 3; -8), С (-1; -3; -6).
3. Найти угол между векторами АВ и ВС, если А (1; 6), В (1; 0), С (-2; 3).
4. Определить угол между векторами АВ и СD, если А (1; -3; -4), В (-1; 0; 2), С (2; -4; -6), D (1; 1; 1).
2. В треугольнике АВС найти величину угла В, если А (0; 5; 0), В (4; 3; -8), С (-1; -3; -6).
3. Найти угол между векторами АВ и ВС, если А (1; 6), В (1; 0), С (-2; 3).
4. Определить угол между векторами АВ и СD, если А (1; -3; -4), В (-1; 0; 2), С (2; -4; -6), D (1; 1; 1).
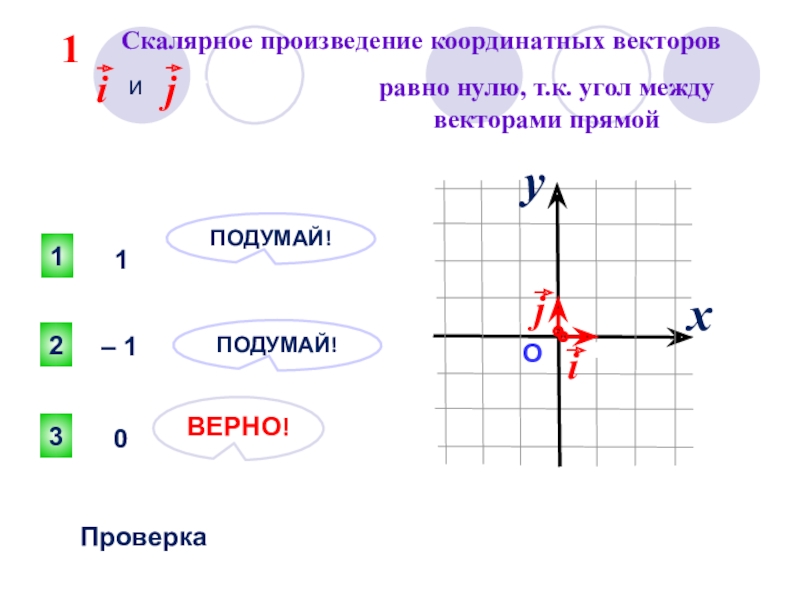
Слайд 17 Скалярное произведение координатных векторов
и :
3
ВЕРНО!
2
1
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
равно нулю, т.к. угол между векторами прямой
1
– 1
0
1
Слайд 191
ВЕРНО!
2
3
ПОДУМАЙ!
Проверка
то векторы и
:
сонаправлены;
противоположно направлены.
перпендикулярны;
3
4
ПОДУМАЙ!
12
3
Слайд 20ПОДУМАЙ!
3
2
1
ПОДУМАЙ!
Проверка
Если
= –20,
x = 4,
y = 5,
то векторы
и :
сонаправлены;
противоположно направлены.
перпендикулярны;
4
5
–20
ВЕРНО!
–1
4
Слайд 213
ВЕРНО!
2
1
ПОДУМАЙ!
ПОДУМАЙ!
Проверка
500
600
1200
Найдите угол между векторами и
, если
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол между векторами тупой
5
Слайд 22 «Синквейн» - французское слово, обозначающее «пять строк».
Правила написания синквейна:
1
строка - заключает в себе одно слово, обычно существительное, которое обозначает объект или предмет, о котором пойдет речь.
2 строка - два слова, чаще всего прилагательные. Они дают описание признаков и свойств выбранного в синквейне предмета или объекта.
3 строка - образована тремя глаголами, описывающими характерные действия объекта.
4 строка - фраза из четырех слов, выражает личное отношение автора синквейна к описываемому предмету или объекту.
5 строка - одно слово, характеризующее суть предмета или объекта.
2 строка - два слова, чаще всего прилагательные. Они дают описание признаков и свойств выбранного в синквейне предмета или объекта.
3 строка - образована тремя глаголами, описывающими характерные действия объекта.
4 строка - фраза из четырех слов, выражает личное отношение автора синквейна к описываемому предмету или объекту.
5 строка - одно слово, характеризующее суть предмета или объекта.
Слайд 23С и н к в е й н
Угол
Острый, прямой
Составляется, строится, вычисляется
Связан
со скалярным произведением
Вектор
Вектор
Слайд 24Домашнее задание
Выучить формулы скалярного произведения векторов и нахождения угла между ними;
Подготовить
кроссворд по теме «Векторы»
