Дисциплина «Математика»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Первообразная функции
Содержание
- 1. Презентация по математике на тему Первообразная функции
- 2. Используемые методы обучения: информационно-коммуникационные технологии
- 3. Цели урока: ОБРАЗОВАТЕЛЬНЫЕ: сформулировать понятие
- 4. План урока1. Организационный момент-3 мин. а)
- 5. Слайд 5
- 6. Разминка.
- 7. Разминка.
- 8. Ответы к домашнему заданию: № 290
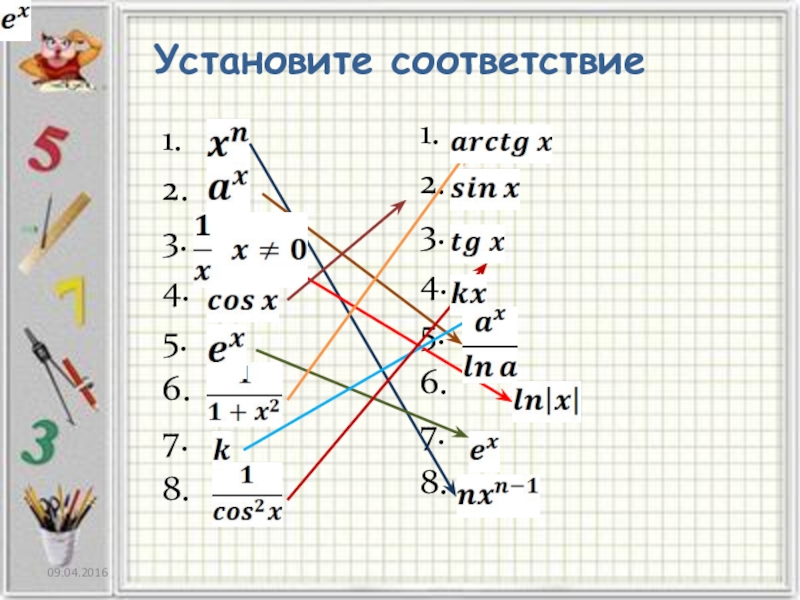
- 9. Установите соответствие1.2.3.4.5.6.7.8. 1.2.3.4.5.6.7.8.
- 10. Установите соответствие1.2.3.4.5.6.7.8. 1.2.3.4.5.6.7.8.
- 11. Математический диктант Чему равна производная функции:1.2.3.4.5.6.Ответы:1.2.3.4.5.6.
- 12. Математический диктант Чему равна производная функции:1.2.3.4.5.6.Ответы:1.2.3.4.5.6.
- 13. Что такое «первообразная» ?В толковом словаре русского
- 14. Слайд 14
- 15. первообразная дляпроизводная из
- 16. Определение первообразной Функция F называется первообразной
- 17. y = f(x) имеет бесконечно много первообразных
- 18. Пример 1Найти первообразную для функции f(x)=x2 Решение:
- 19. Пример 2Найти первообразную для функции Решение :
- 20. Пример 3 Является ли функция функция
- 21. Три правила нахождения первообразныхПравило 1Если F есть
- 22. Правило 2Если F есть первообразная для f,
- 23. Слайд 23
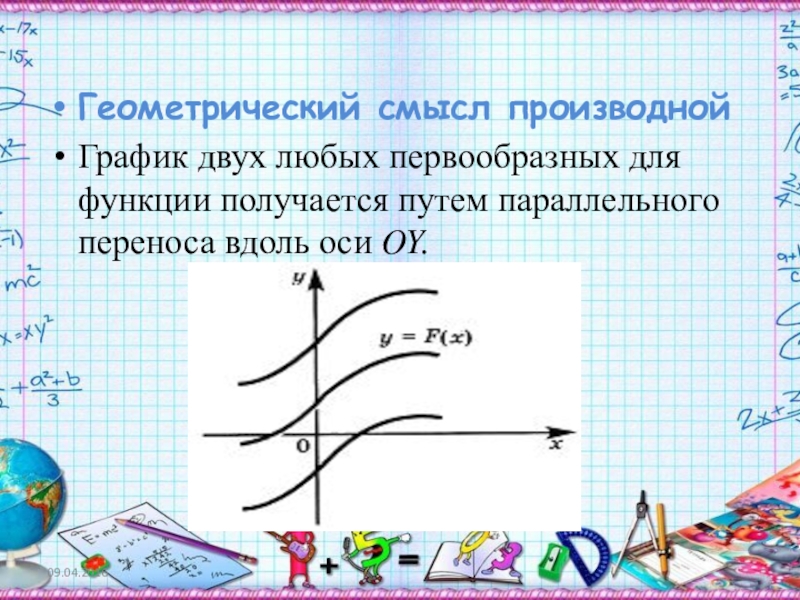
- 24. Геометрический смысл производнойГрафик двух любых первообразных для функции получается путем параллельного переноса вдоль оси OY.
- 25. Таблица первообразных
- 26. :Примеры:Дана функция f(x) = -x3, найти F(x)
- 27. :Примеры:Дана функция f(x) = 1/x2, найти F0(x) на (0; ), F(1) = 1
- 28. Найдите общий вид первообразных для функции: 1. 2.
- 29. Домашнее
- 30. Рефлексия 1. Сегодня я узнал(а)- 2. Было
- 31. Спасибо за внимание
Слайд 3Цели урока: ОБРАЗОВАТЕЛЬНЫЕ: сформулировать понятие о первообразной функции; изучить основные свойства первообразной;
Слайд 4План урока
1. Организационный момент-3 мин.
а) взаимное приветствие;
б)
в) постановка цели занятия перед студентами;
г) готовность и настрой студентов на работу в течении урока.
2. Актуализация теоретических знаний – 15 мин.
3. Изложение нового материала – 20 мин.
4. Закрепление и совершенствование знаний – 35 мин.
5. Итоги урока – 5 мин.
6. Домашнее задание – 2 мин.
Слайд 5 Эпиграф:
Три пути ведут к
путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький.
Конфуций .
Слайд 13Что такое «первообразная» ?
В толковом словаре русского языка, под редакцией Д.Н.
являющийся началом, первым этапом какого-нибудь действия, процесса, первым видом, первой формой развития кого(чего)-нибудь.
Слайд 16
Определение первообразной
Функция F называется первообразной для функции f на
F(x) = f(x)
Слайд 17
y = f(x) имеет бесконечно много первообразных вида y = F(x)+C,
C - произвольное число
f(x) = 2x
F1(x) = x2 +C
F2(x) = x2 + 1+C
F3(x) = x2 + 5+C
F1'(x) = 2x
F2'(x) = 2x
F3'(x) = 2x
Неоднозначность первообразной
Слайд 20Пример 3
Является ли функция функция
первообразной для
на промежутке (-; ) ?
Решение:
Слайд 21Три правила нахождения первообразных
Правило 1
Если F есть первообразная для f, а
(F + G) = F + G = f + g
Пример 4
Дана функция f(x) = x3 + 1/x2, найти F(x)
Слайд 22Правило 2
Если F есть первообразная для f, а k - постоянная,
(kF) = kF = kf
Пример 5
f(x) = 5cosx, найти F(x)
Слайд 23
Правило 3
Если F(x) есть первообразная для f(x), а k и b – постоянные, причем k 0, то есть первообразная для f(kx + b):
Пример 6


























![Презентация по математике на тему Первообразная функции Домашнее задание: [3]- № 477, 480, 485, 490, 491, 495. Домашнее задание: [3]- № 477, 480, 485, 490, 491, 495.](/img/thumbs/31154d83bf330232e25bf97c1f659c09-800x.jpg)







