- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Графическое решение уравнений и неравенств
Содержание
- 1. Презентация по математике на тему Графическое решение уравнений и неравенств
- 2. При решении уравнений и неравенств часто возникают
- 3. Графическое решение квадратного уравнения: Рассмотрим приведённое
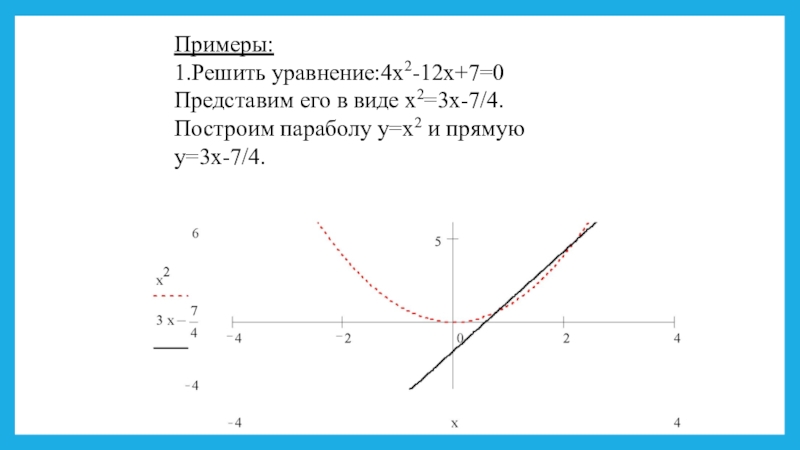
- 4. Примеры:1.Решить уравнение:4x2-12x+7=0Представим его в виде x2=3x-7/4.Построим параболу y=x2 и прямую y=3x-7/4.
- 5. Системы уравнений. Графиком уравнения с двумя переменными
- 6. Тригонометрические уравнения: Тригонометрические уравнения решают как аналитически,
- 7. Применение графиков в решении неравенств.Неравенства с модулем.Неравенства с параметрами.Тригонометрические неравенства
- 8. Решение уравнений и неравенств графическим способом
- 9. Заключение При решении уравнений и неравенств развиваются
При решении уравнений и неравенств часто возникают трудности, связанные со следующими особенностями: незнание четкого алгоритма решения уравнений, неравенств и их систем; при решении уравнений и неравенств, ученики производят преобразования, которые не равносильны исходным уравнениям и неравенствам;
Слайд 2При решении уравнений и неравенств часто возникают трудности, связанные со следующими
особенностями:
незнание четкого алгоритма решения уравнений, неравенств и их систем;
при решении уравнений и неравенств, ученики производят преобразования, которые не равносильны исходным уравнениям и неравенствам;
при решении показательного уравнения и неравенства введением новой переменной забывают возвращаться к обратной замене.
незнание четкого алгоритма решения уравнений, неравенств и их систем;
при решении уравнений и неравенств, ученики производят преобразования, которые не равносильны исходным уравнениям и неравенствам;
при решении показательного уравнения и неравенства введением новой переменной забывают возвращаться к обратной замене.
Слайд 3Графическое решение квадратного уравнения:
Рассмотрим приведённое квадратное уравнение : x2+px+q=0;
Перепишем его
так:x2=-px-q.(1)
Построим графики зависимостей:y=x2 и y=-px-q.
График первой зависимости нам известен, это есть парабола; вторая зависимость- линейная; её график есть прямая линия. Из уравнения (1) видно, что в том случае, когда х является его решением, рдинаты точек обоих графиков равны между собой. Значит, данному значению х соответствует одна и та же точка как на параболе, так и на прямой, то есть парабола и прямая пересекаются в точке с абциссой х.
Построим графики зависимостей:y=x2 и y=-px-q.
График первой зависимости нам известен, это есть парабола; вторая зависимость- линейная; её график есть прямая линия. Из уравнения (1) видно, что в том случае, когда х является его решением, рдинаты точек обоих графиков равны между собой. Значит, данному значению х соответствует одна и та же точка как на параболе, так и на прямой, то есть парабола и прямая пересекаются в точке с абциссой х.
Слайд 4Примеры:
1.Решить уравнение:4x2-12x+7=0
Представим его в виде x2=3x-7/4.
Построим параболу y=x2 и прямую y=3x-7/4.
Слайд 5Системы уравнений.
Графиком уравнения с двумя переменными называется множество точек координатной плоскости,
координаты которых обращают уравнение в верное равенство. Графики уравнений с двумя переменными весьма разнообразны. Например, графиком уравнения 2х+3у=15 является прямая, уравнения у=0.5х2 –2 –парабола, уравнения х2 +у2=4 – окружность, и т.д..
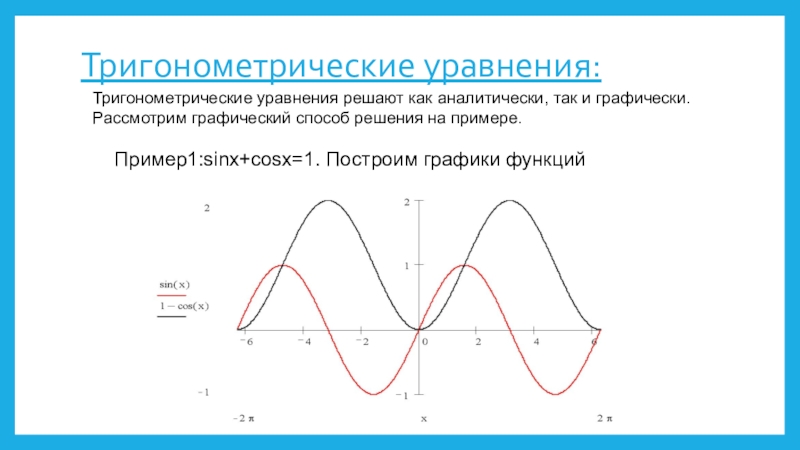
Слайд 6Тригонометрические уравнения:
Тригонометрические уравнения решают как аналитически, так и графически. Рассмотрим графический
способ решения на примере.
Пример1:sinx+cosx=1. Построим графики функций
Слайд 7Применение графиков в решении неравенств.
Неравенства с модулем.
Неравенства с параметрами.
Тригонометрические неравенства
Слайд 9Заключение
При решении уравнений и неравенств развиваются навыки систематизации, логического мышления при
выборе правильного метода решения, повышает творческие и умственные способности. Их изучение очень важно в курсах школьной математики и математики в колледже, т.к. примеры, содержащие показательные уравнение и неравенства, встречаются в экзаменационных заданиях, не только в составе показательных уравнений и неравенств, но и в системах и смешанных уравнениях.