- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему
Содержание
- 1. Презентация по математике на тему
- 2. ПрямоугольникиВ повседневной жизни человека окружают прямоугольники. И
- 3. Календари,Книги
- 4. Тетради
- 5. Дома
- 6. Письменный Стол, классная доска, портфель
- 7. Двери
- 8. Окна
- 9. Шкафы
- 10. Мониторы
- 11. Системные Блоки
- 12. Жалюзи
- 13. Сейфы
- 14. Прямоугольник – это параллелограмм, у которого все углы прямые.Диагонали прямоугольника равны.Прямоугольник
- 15. Элементы прямоугольника Четыре точки- вершиныЧетыре отрезка, попарно
- 16. Прямоугольник обладает всеми свойствами параллелограмма (Свойство -
- 17. Диагонали прямоугольника Длины диагоналей прямоугольника равны.Диагонали прямоугольника делятся точкой пересечения пополам.Длина диагонали прямоугольника вычисляется по теореме Пифагора
- 18. Признаки прямоугольника (Признак - это характерная особенность,
- 19. Формула площади прямоугольника Площадь прямоугольника равна произведению длин
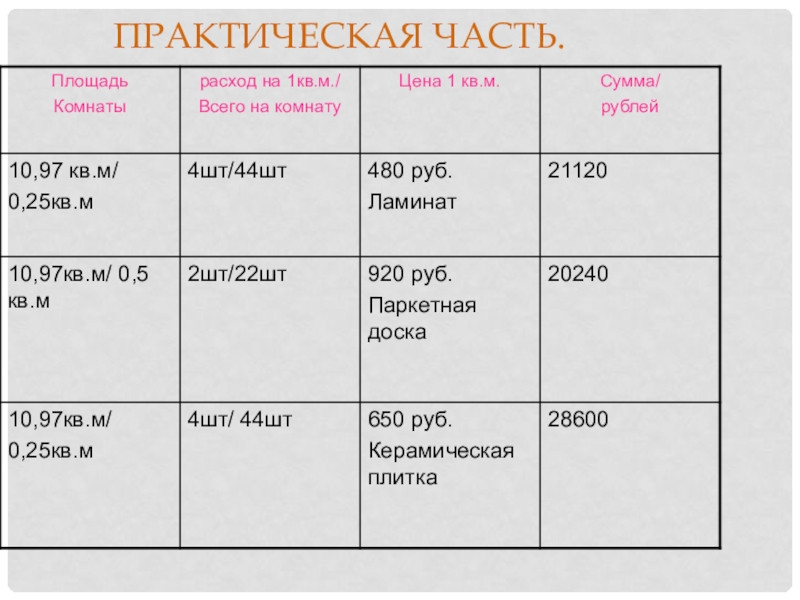
- 20. Практическая часть.
- 21. Периметр прямоугольникаПериметр прямоугольника равен удвоенной сумме длин его ширины и длиныa, b – длина и ширина прямоугольника. P=2a+2bилиP=2(a+b)
- 22. Задача№1 в тетради В детском
- 23. Решение задачи №11) 2(14+26)=80м-длина проведенной линии баскетбольной
- 24. Задача в тетради №2Диагонали прямоугольника АВСD пересекаются
- 25. Решение задачи №2Диагонали прямоугольника в точке пересечения
- 26. Прямоугольный треугольникКакой треугольник называется прямоугольным?Как называются стороны
- 27. Теорема пифагора-важнейшее утверждение геометрии
- 28. Пифагор самосскийПифагор-едва ли не самый популярный ученый
- 29. Пифагор Самосский-древнегреческий ученый (570-490г. до нашей эры)
- 30. Биография Пифагора Великий ученый Пифагор Самосский
- 31. Отцом Пифагора был Мнесарх, резчик по драгоценным
- 32. По совету Фалеса двадцатилетний Пифагор принимает решение
- 33. В Вавилоне Пифагор прожил еще 12 лет.
- 34. Пифагорейская школа Пентаграмма у пифагорейцев — символ
- 35. Открытия пифагорейцев пифагоровы тройки Известна задача Пифагора
- 36. Открытия пифагорейцев совершенные числаВажное достижение пифагорейцев-открытие совершенных
- 37. Именем Пифагора назван кратер на Луне
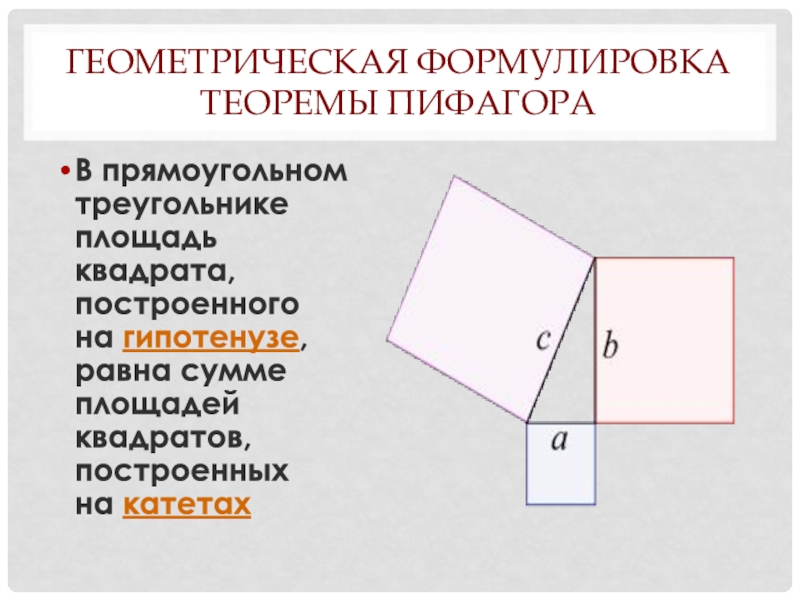
- 38. Геометрическая формулировка теоремы ПифагораВ прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах
- 39. Алгебраическая формулировка теоремы ПифагораВ прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов
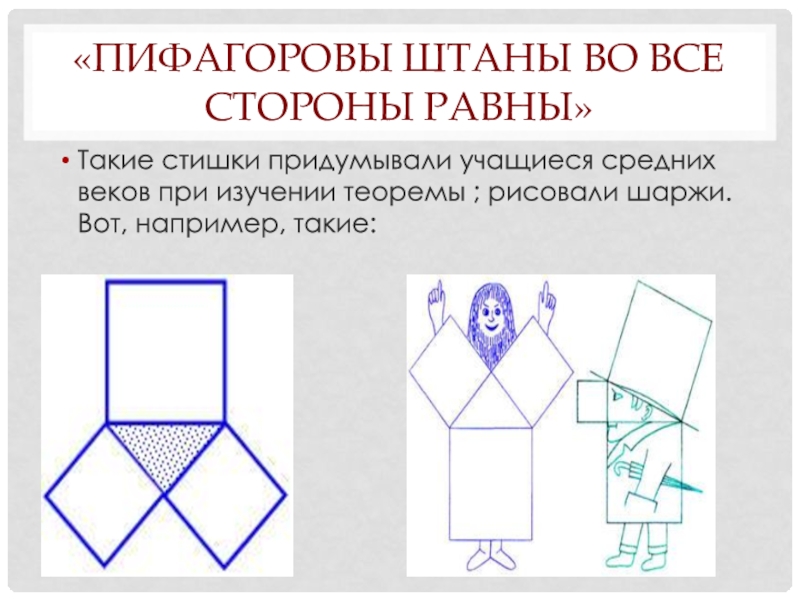
- 40. «Пифагоровы штаны во все стороны равны» Такие
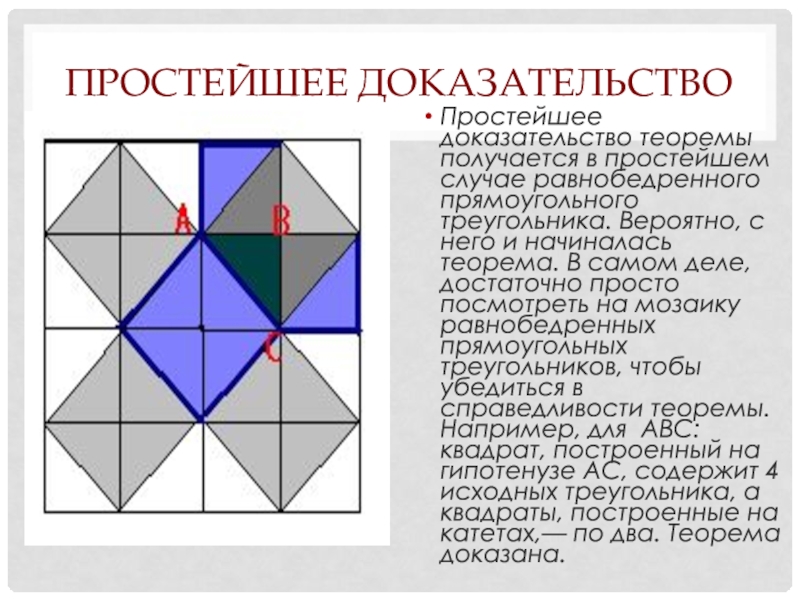
- 41. Простейшее доказательствоПростейшее доказательство теоремы получается в простейшем
- 42. По теореме ПифагораРешение задач для подготовки к ОГЭ
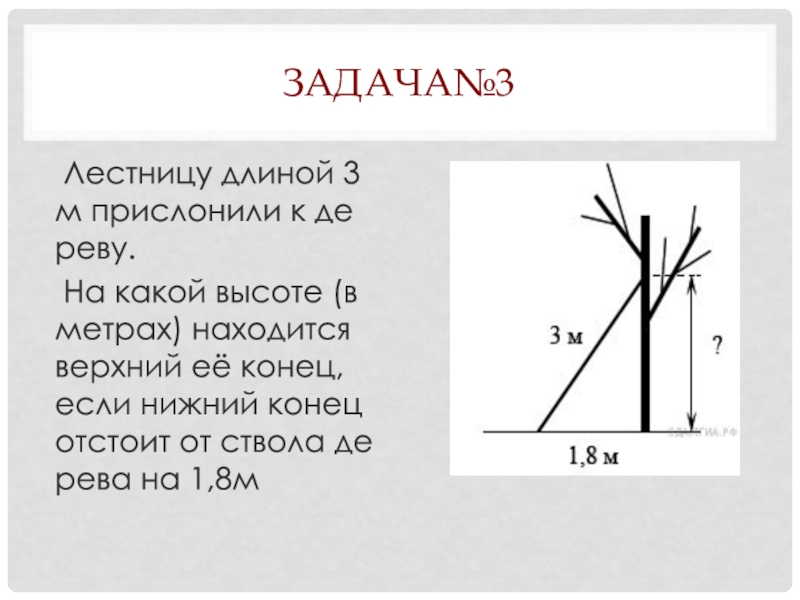
- 43. Задача№3 Лестницу длиной 3 м прислонили к дереву.
- 44. РешениеЗадача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он равен: ----
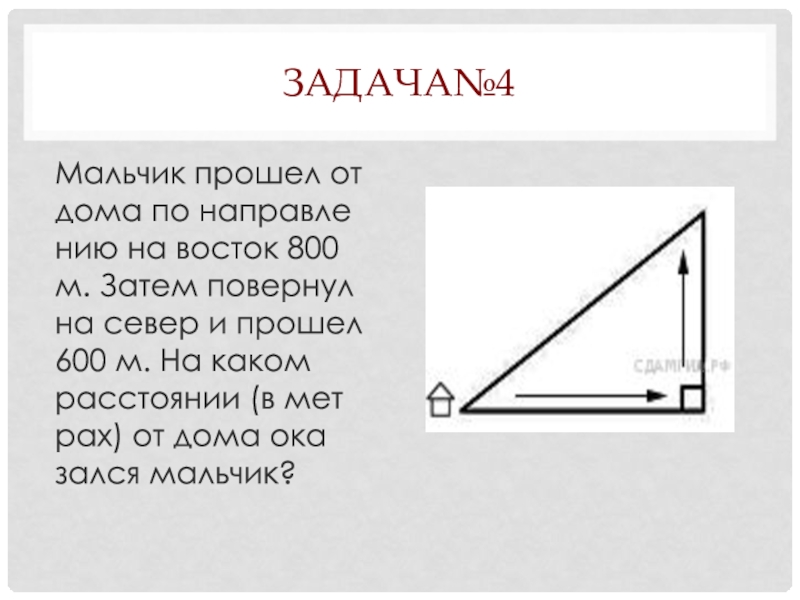
- 45. Задача№4Мальчик прошел от дома по направлению на
- 46. РешениеМальчик идёт вдоль сторон прямоугольного треугольника поэтому, искомое расстояние можно найти по теореме Пифагора:+
- 47. Спасибо за урок!!!
- 48. С наступающим 2015 годом
Слайд 1Тема урока:
«Свойства прямоугольника в задачах»
" Я думаю, что никогда до
Слайд 2Прямоугольники
В повседневной жизни человека окружают прямоугольники. И это неспроста. В построении
Предметы, окружающие человека, состоят из множества прямоугольников.
Слайд 14Прямоугольник – это параллелограмм,
у которого все углы прямые.
Диагонали прямоугольника равны.
Прямоугольник
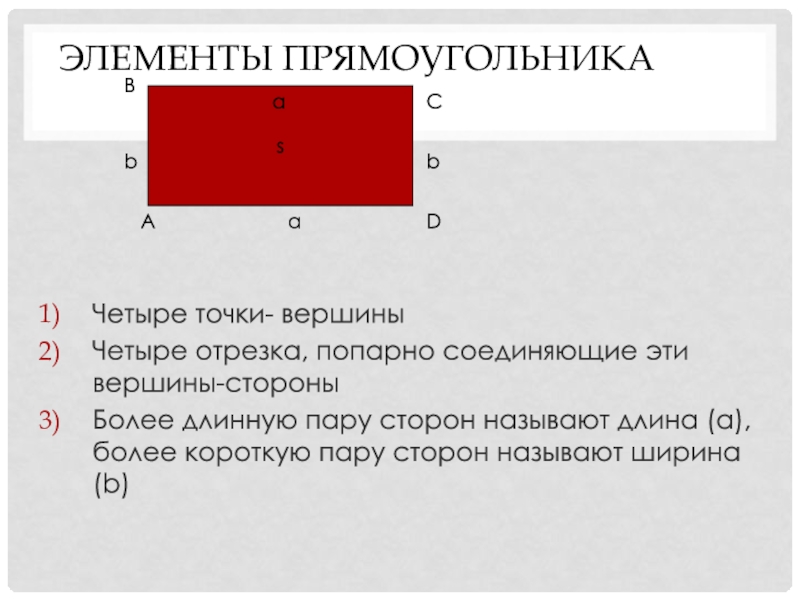
Слайд 15Элементы прямоугольника
Четыре точки- вершины
Четыре отрезка, попарно соединяющие эти вершины-стороны
Более длинную пару
s
A
B
C
D
a
b
a
b
Слайд 16Прямоугольник обладает всеми свойствами параллелограмма (Свойство - это характерная особенность, присущая только
Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (по теореме Пифагора).
Стороны прямоугольника являются его высотами.
Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности (радиус равен половине диагонали).
Слайд 17Диагонали прямоугольника
Длины диагоналей прямоугольника равны.
Диагонали прямоугольника делятся точкой пересечения пополам.
Длина диагонали
Слайд 18Признаки прямоугольника (Признак - это характерная особенность, по которой ищут в многообразии
Если диагонали параллелограмма равны-это прямоугольник
Если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон-это прямоугольник
Если углы параллелограмма равны 90 градусам-это прямоугольник
Слайд 19Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a
где S - Площадь прямоугольника,
a, b - длины сторон прямоугольника.
Слайд 21Периметр прямоугольника
Периметр прямоугольника равен удвоенной сумме длин его ширины и длины
a, b
P=2a+2b
или
P=2(a+b)
Слайд 22Задача№1 в тетради
В детском оздоровительном лагере размечают
Смежные стороны баскетбольной площадки: 14 и 26 м, а волейбольной: 9 и 18 м.
Чтобы провести линию длиной 1м нужно 40г краски. Сколько нужно краски, чтобы обвести линией обе площадки?
Слайд 23Решение задачи №1
1) 2(14+26)=80м-длина проведенной линии баскетбольной площадки.
2) 2(9+18)= 54 м
3)80+54=134 м-длина всей линии
4)134*40=5360г- масса необходимой краски
Ответ: 5360г.
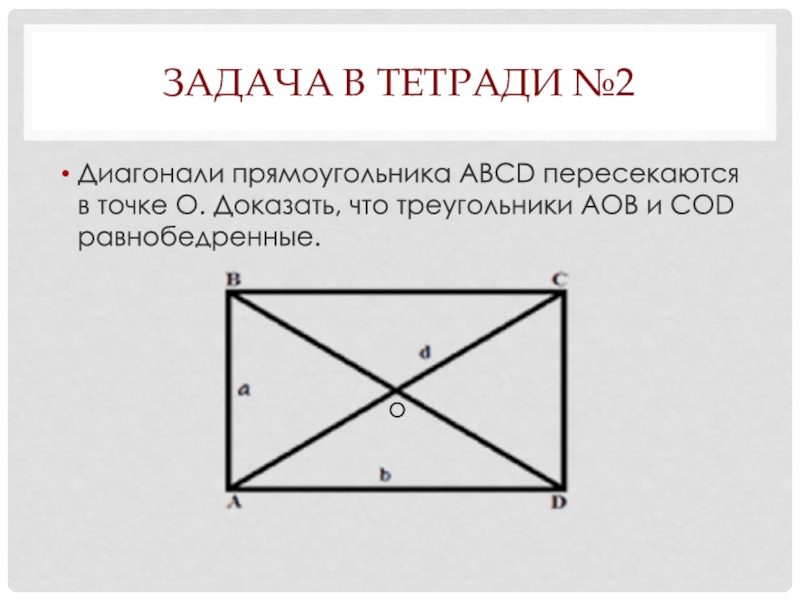
Слайд 24Задача в тетради №2
Диагонали прямоугольника АВСD пересекаются в точке О. Доказать,
О
Слайд 25Решение задачи №2
Диагонали прямоугольника в точке пересечения делятся пополам, но у
Значит ∆ АОВ равнобедренный, т.к. АО=ОВ, ∆ СОD равнобедренный, т.к. СО=ОD.
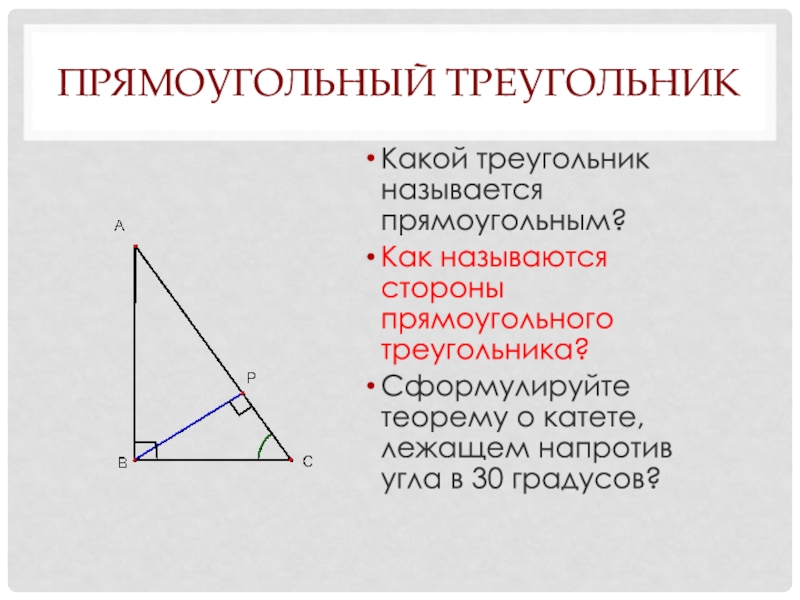
Слайд 26Прямоугольный треугольник
Какой треугольник называется прямоугольным?
Как называются стороны прямоугольного треугольника?
Сформулируйте теорему о
Слайд 28Пифагор самосский
Пифагор-едва ли не самый популярный ученый за всю историю человечества.
Трудно
В настоящее время зафиксировано 367 различных доказательств этой теоремы
Слайд 30Биография Пифагора
Великий ученый Пифагор Самосский родился на острове Самосе
Слайд 31Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери
По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Увлекался музыкой и поэзией. Неугомонному воображению Пифагора стало тесно на маленьком острове.
Мудрый учитель Ферекид сказал: «Ты вырос из Самоса, отправляйся путешествовать. Помни: путешествие и память-суть два средства, возвышающие человека и открывающие ему врата мудрости»
Для жителей Самоса все дороги вели в Милет-греческую колонию. Там Пифагор встречается с Фалесом, мудрецом, слава о котором гремела по всей Элладе.
Слайд 32По совету Фалеса двадцатилетний Пифагор принимает решение отправиться в Египет. Там
Пифагор овладевает тайнами египетских жрецов и достигает высших ступеней храмовой иерархии.
В 526г. до н.э. в Египет вторглись войска персидского царя Камбиза, и Пифагор вместе с другими жрецами попал в плен и оказался в Вавилоне.
Слайд 33В Вавилоне Пифагор прожил еще 12 лет. Ничего нового жрецы уже
Там Пифагор собирает вокруг себя юношей из благородных семей и ведет тайные беседы.
Но правитель острова Поликрат приказывает своим людям следить за Пифагором. Возмущенный ученый навсегда покидает остров и поселяется в южной Италии в городе Кротоне
Слайд 34Пифагорейская школа
Пентаграмма у пифагорейцев — символ здоровья и совершенства. Они
В Кротоне Пифагор основал сообщество своих учеников и последователей-пифагорейскую школу.
Пифагорейцы узнавали друг друга по звездчатому пятиугольнику-пентаграмме
Нравственные принципы и правила, проповедуемые Пифагором и сегодня достойны подражания. Он учил: беги от всякой хитрости, отсекай любым оружием от тела болезнь, от души – невежество, от утробы-роскошь, от города –смуту, от семьи-ссору.
Слайд 35Открытия пифагорейцев
пифагоровы тройки
Известна задача Пифагора или пифагоровы тройки. Общее решение задачи
Прямоугольный треугольник со сторонами 3,4,5 использовали «натягиватели веревок»-гарпедонапты.
Каждый год Нил разливался и уничтожал границы земельных участков, а землемеры с помощью веревок и узлов размечали прямоугольные участки. Они брали веревку длиной 12м и через 3,4,5 м привязывали цветную полоску, угол между 3и 4 был прямой
Слайд 36Открытия пифагорейцев
совершенные числа
Важное достижение пифагорейцев-открытие совершенных чисел. Натуральное число равное сумме
И самое важное – это терема Пифагора. Изучение вавилонских и древнекитайских рукописей показало, что утверждение теоремы было известно задолго до Пифагора. Его заслуга в том, что он доказал эту теорему
Слайд 38Геометрическая формулировка теоремы Пифагора
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна
Слайд 39Алгебраическая формулировка теоремы Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме
Слайд 40«Пифагоровы штаны во все стороны равны»
Такие стишки придумывали учащиеся средних
Слайд 41Простейшее доказательство
Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника.
Слайд 43Задача№3
Лестницу длиной 3 м прислонили к дереву.
На какой высоте (в
Слайд 44Решение
Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он
--
--
Слайд 45Задача№4
Мальчик прошел от дома по направлению на восток 800 м. Затем
Слайд 46Решение
Мальчик идёт вдоль сторон прямоугольного треугольника поэтому, искомое расстояние можно найти
+