- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на теме:Симметрии осевая и центральная
Содержание
- 1. Презентация по математике на теме:Симметрии осевая и центральная
- 2. Слово «симметрия» греческое ( συμμετρία), оно означает
- 3. Осевая симметрияФигура называется симмет-ричной относительно прямой a,
- 4. Осевая симметрия Точки А
- 5. Центральная симметрия (алгоритм построения) АА1ОТочка А
- 6. Осевая симметрия (алгоритм построения) АА1а1) Проведём
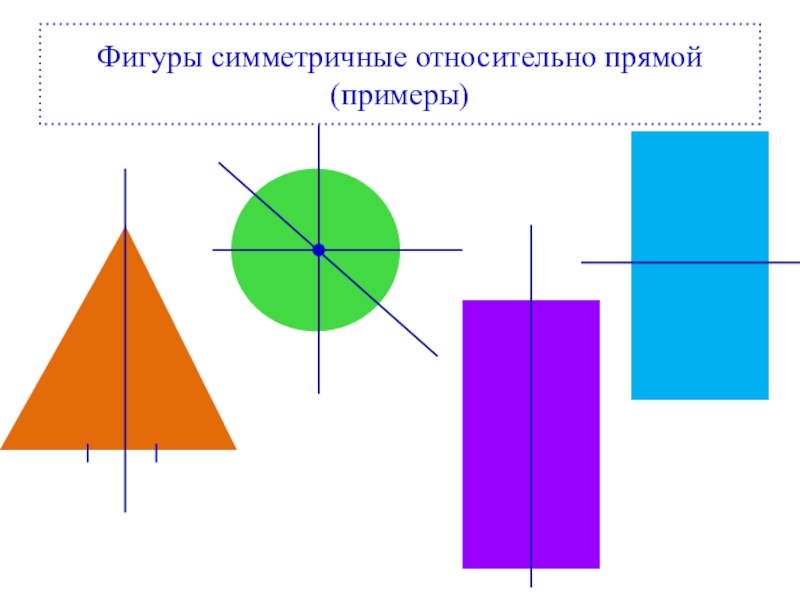
- 7. Фигуры симметричные относительно прямой (примеры)
- 8. Ось симметрии имеют плоские и пространственные
- 9. BCАC1B1A1аОсевая симметрия Задание.
- 10. Задание.
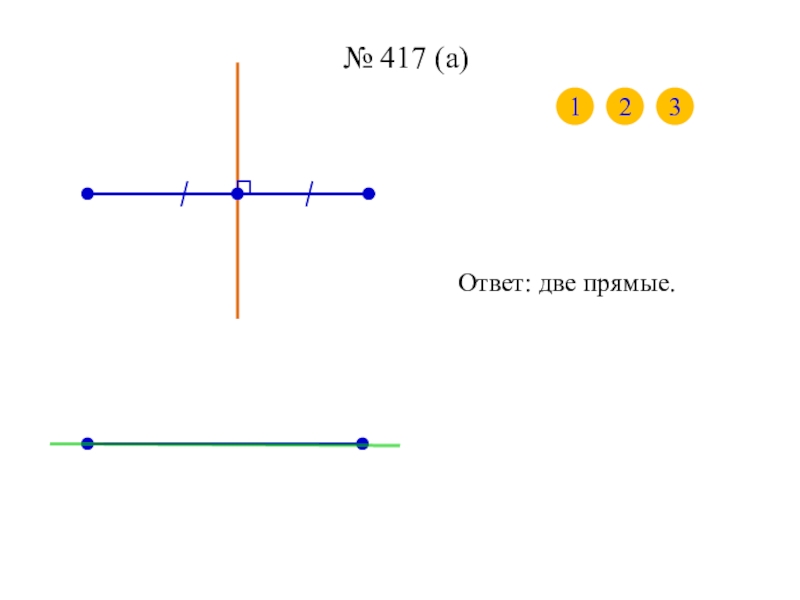
- 11. № 417 (а)123Ответ: две прямые.
- 12. № 417 (б)12Ответ: бесконечно много осей симметрии
- 13. Центральная симетрия Центральная симметрия является одним из
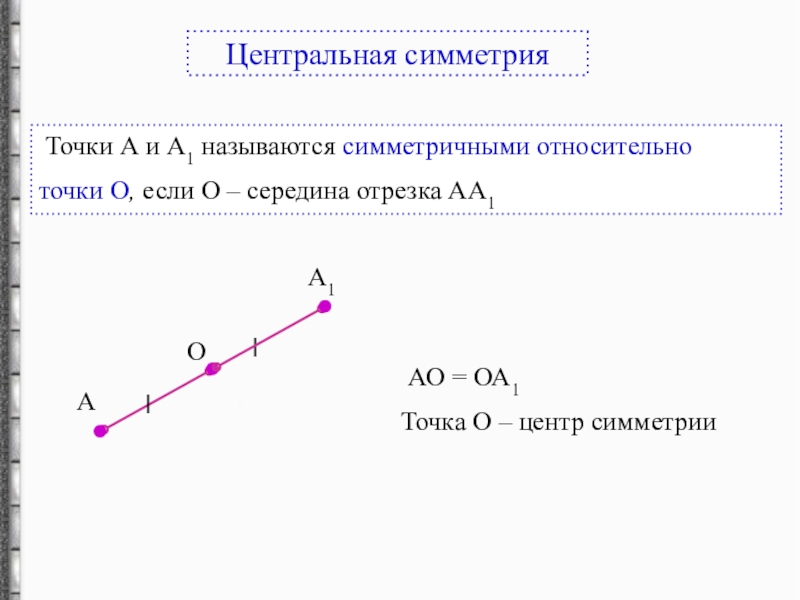
- 14. Точки А и А1 называются симметричными
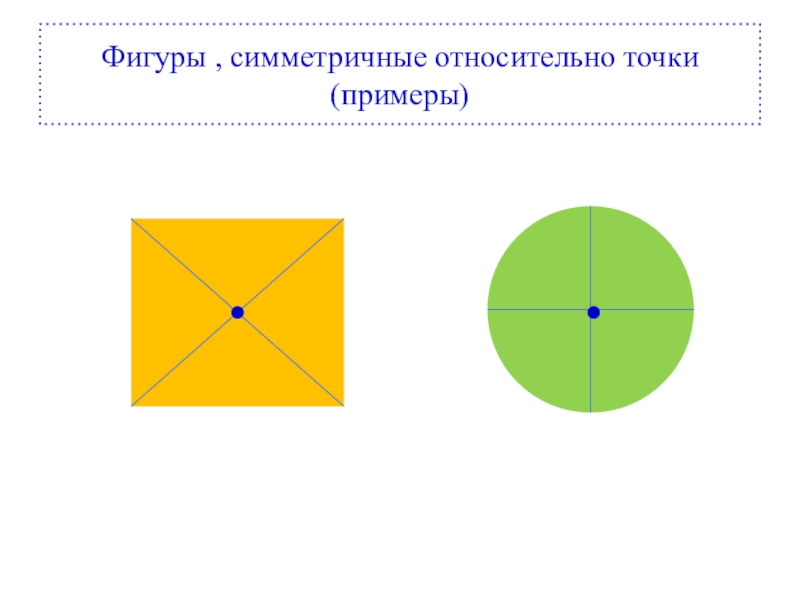
- 15. Фигуры , симметричные относительно точки (примеры)
- 16. Если внимательно рассмотреть данные орнаменты и фигуры,
- 17. ВАС ОЦентральная симметрияВ1А1С1Задание.
- 18. Задание .
- 19. Распределите данные фигуры по трём столбикам
- 20. 1232, 4, 6, 8, 9, 11, 13,
Слайд 2 Слово «симметрия» греческое ( συμμετρία), оно означает “соразмерность, пропорциональность, одинаковость в
Слайд 3Осевая симметрия
Фигура называется симмет-ричной относительно прямой a, если для каждой точки
Рассмотрите данные фигуры. Каждая из них состоит как бы из двух полови-нок, одна из ко-торых является зеркальным отра-жением другой. Каждую из этих фигур можно сог-нуть «пополам» так, что эти поло-винки совпадут. Говорят, что эти фигуры симмет-ричны относи-тельно прямой – линии сгиба.
Слайд 4
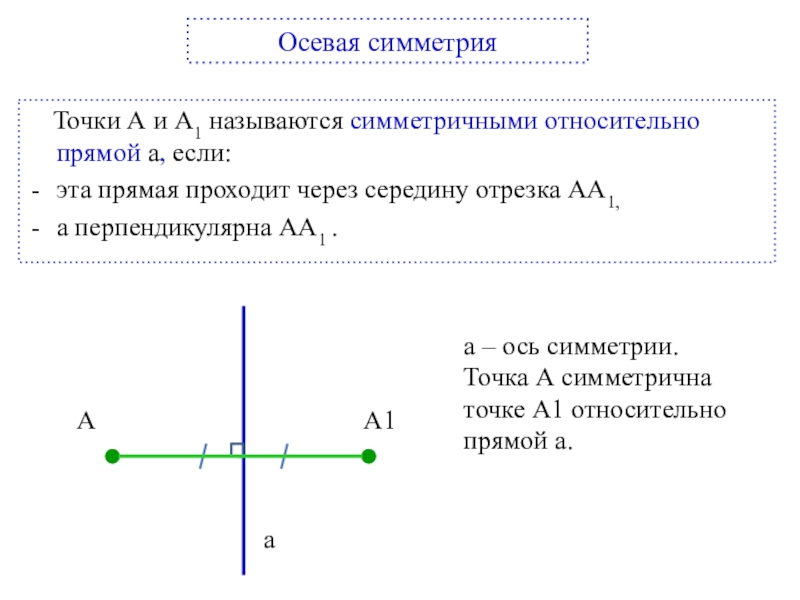
Осевая симметрия
Точки А и А1 называются симметричными относительно прямой
эта прямая проходит через середину отрезка АА1,
а перпендикулярна АА1 .
А
А1
а
a – ось симметрии.
Точка А симметрична точке А1 относительно прямой а.
Слайд 5
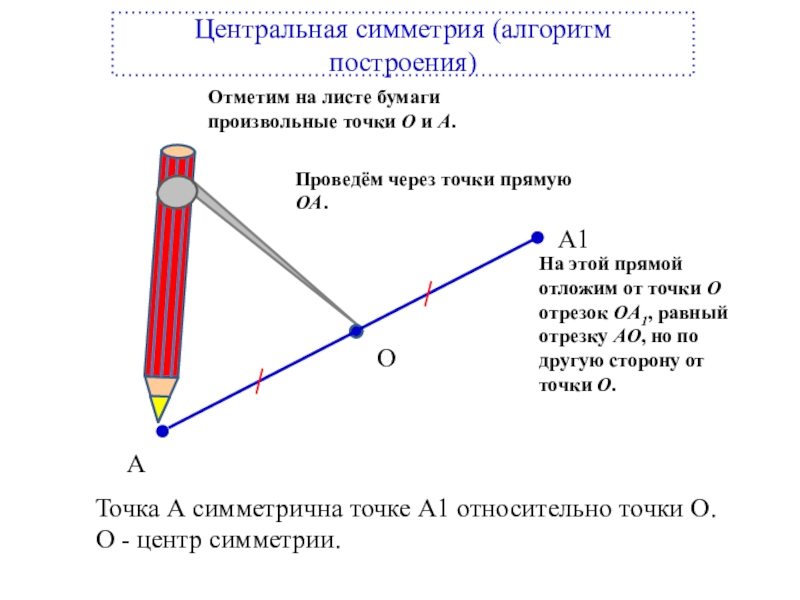
Центральная симметрия (алгоритм построения)
А
А1
О
Точка А симметрична точке А1 относительно точки О.
О - центр симметрии.
Отметим на листе бумаги произвольные точки O и A.
Проведём через точки прямую OA.
На этой прямой отложим от точки O отрезок OA1, равный отрезку AO, но по другую сторону от точки O.
Слайд 6
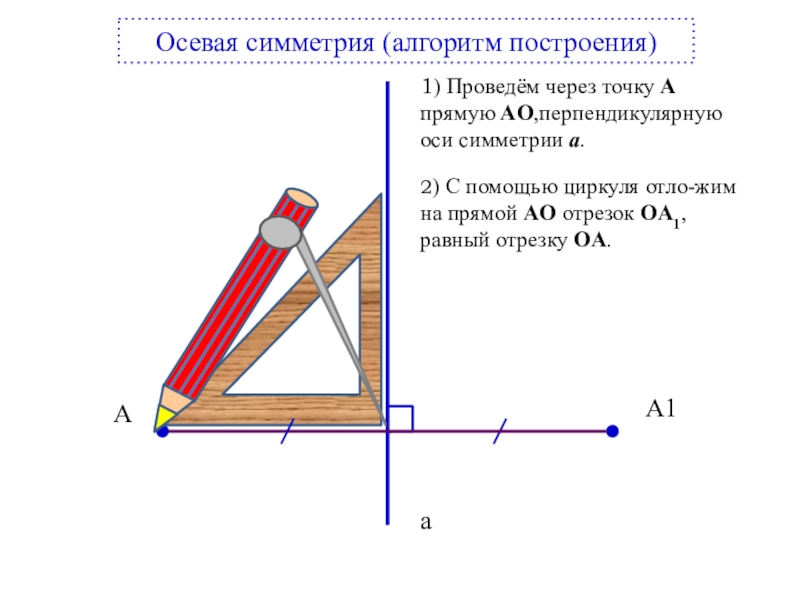
Осевая симметрия (алгоритм построения)
А
А1
а
1) Проведём через точку А прямую АO,перпендикулярную оси
2) С помощью циркуля отло-жим на прямой АO отрезок OА1, равный отрезку OА.
Слайд 8Ось симметрии имеют плоские и пространственные фигуры. Например:
Некоторые фигуры имеют
Задание. Из данных фигур выберите те, которые имеют ось симметрии. Есть ли среди них такие, которые имеют более одной оси симметрии?
На листе бумаги изображена «ёлочка». Концы её нижних «веток» обозначены буквами A и A1. Если перегнуть «ёлочку» по прямой l, то точки A и A1 совпадут. Если посмотреть на рисунок сверху, то точки A и A1 будут расположены на пер-пендикуляре к прямой l по разные стороны и на равных расстояниях от неё. Такие точки называют симмет-ричными относительно пря-мой l .
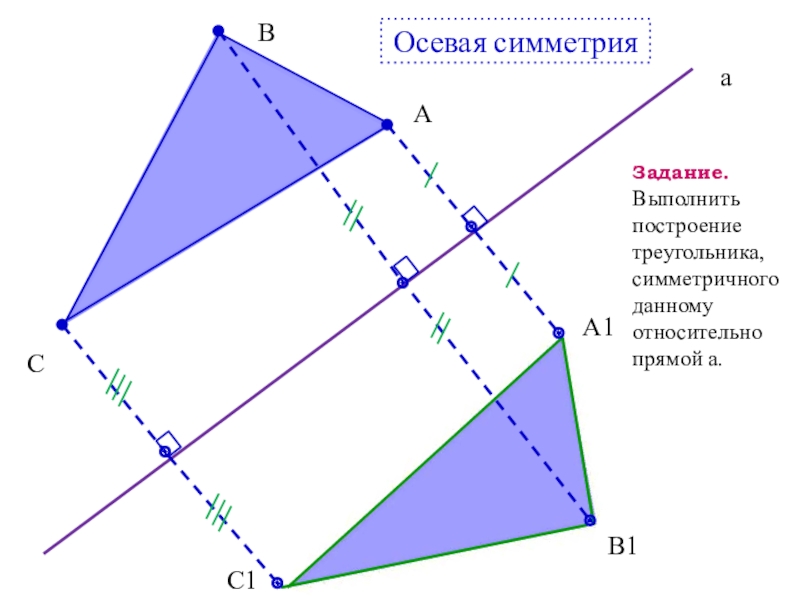
Слайд 9B
C
А
C1
B1
A1
а
Осевая симметрия
Задание.
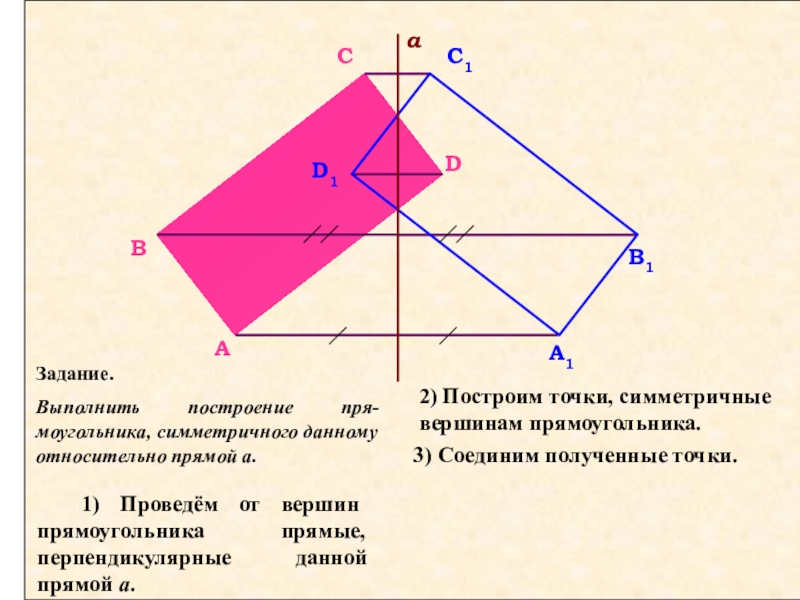
Слайд 10Задание.
Выполнить
1) Проведём от вершин прямоугольника прямые, перпендикулярные данной прямой a.
B
B1
a
A
C
D
A1
C1
D1
2) Построим точки, симметричные вершинам прямоугольника.
3) Соединим полученные точки.
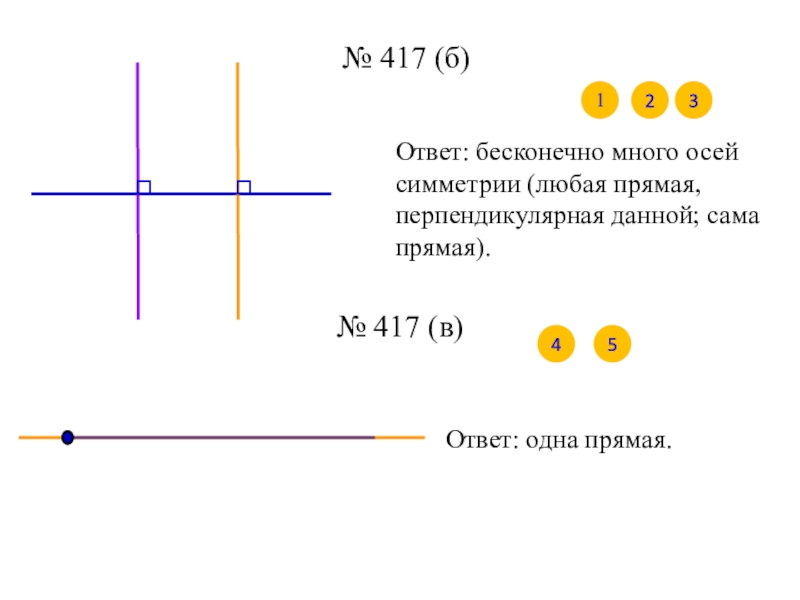
Слайд 12№ 417 (б)
1
2
Ответ: бесконечно много осей симметрии (любая прямая, перпендикулярная данной;
№ 417 (в)
Ответ: одна прямая.
3
4
5
Слайд 13Центральная симетрия
Центральная симметрия является одним из видов симметрии.
Фигура называется симметричной
Слайд 14 Точки А и А1 называются симметричными относительно
точки О, если
А
А1
О
АО = ОА1
Точка О – центр симметрии
Центральная симметрия
Слайд 16Если внимательно рассмотреть данные орнаменты и фигуры, можно заметить, что все
Задание. На рисунке изображены различные геометричес-кие фигуры. Выберите из них те, которые име-ют центр симметрии, и изобразите их в тет-ради. Отметьте центр симметрии и точки, симметричные отмечен-ным точкам.
Слайд 17В
А
С
О
Центральная симметрия
В1
А1
С1
Задание.
Выполнить построение треугольника, симметричного данному, относительно точки O.
Слайд 18Задание .
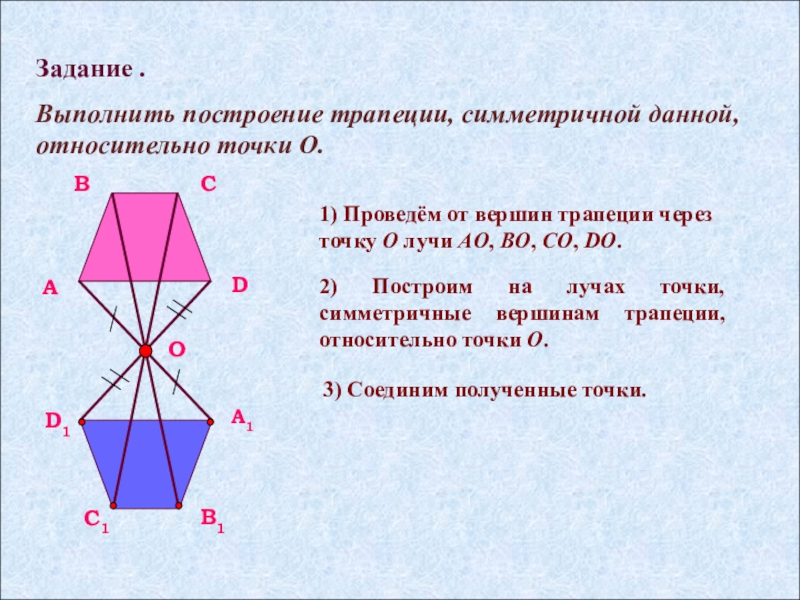
Выполнить построение трапеции, симметричной данной, относительно точки O.
A
B
C
D
A1
B1
C1
D1
O
1) Проведём от вершин трапеции через точку O лучи AO, BO, CO, DO.
2) Построим на лучах точки, симметричные вершинам трапеции, относительно точки O.
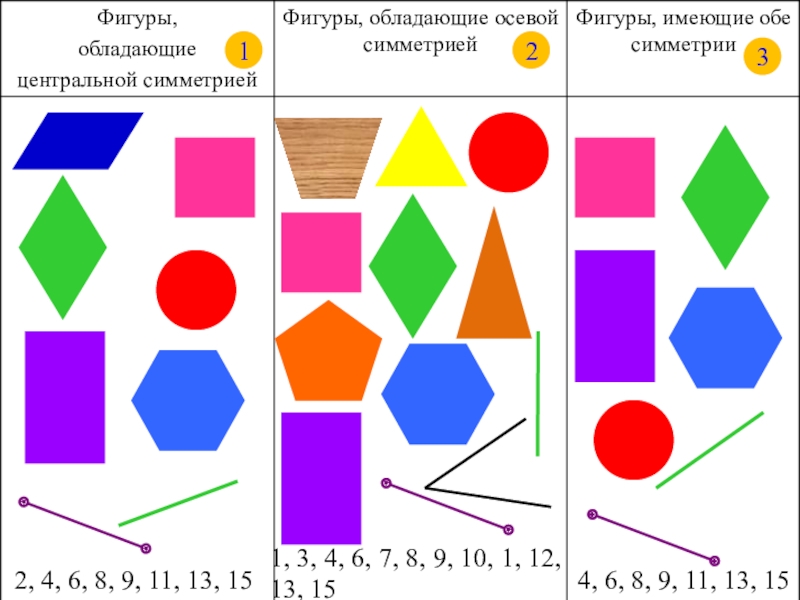
Слайд 19 Распределите данные фигуры по трём столбикам таблицы:
«Фигуры, обладающие центральной
«Фигуры, обладающие осевой симметрией»,
«Фигуры, имеющие обе симметрии».
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15