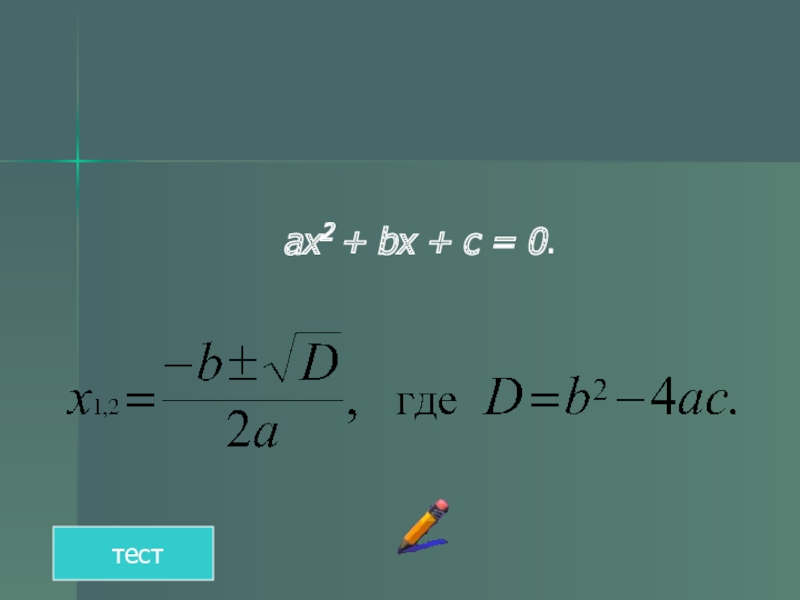орта білім беретін мектеп»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Квадратные уравнения
Содержание
- 1. Презентация по математике Квадратные уравнения
- 2. Өзінді тексер!
- 3. Квадрат теңдеуах2 + вх + с =
- 4. Квадрат теңдеудің дискриминанты ах2
- 5. Егер D > 0 ах2 + bх
- 6. Егер D = 0 ах2 + bх + с = 0 теңдеудің бір шешімі бар:
- 7. Егер D < 0 ах2 + bх + с = 0 теңдеудің түбірі болмайды :
- 8. ах2 + bх + с = 0. тест
- 9. Тест1. х2-5х-6=0 дискриминанты табыңдар.0-6125-549Келесі сұрақ
- 10. 2. D < 0 болса теңдеудің неше шешімі бар?Үш түбірБір түбірЕкі түбіріТүбірі жоқКелесі сұрақ
- 11. 2у2-9у+10=0 теңдеудің түбірлерін табыңдар.у1=-2; у2=-2,5Түбірі жоқу1=2; у2=-2,5у1=2; у2=2,5
- 12. Слайд 12
- 13. Слайд 13
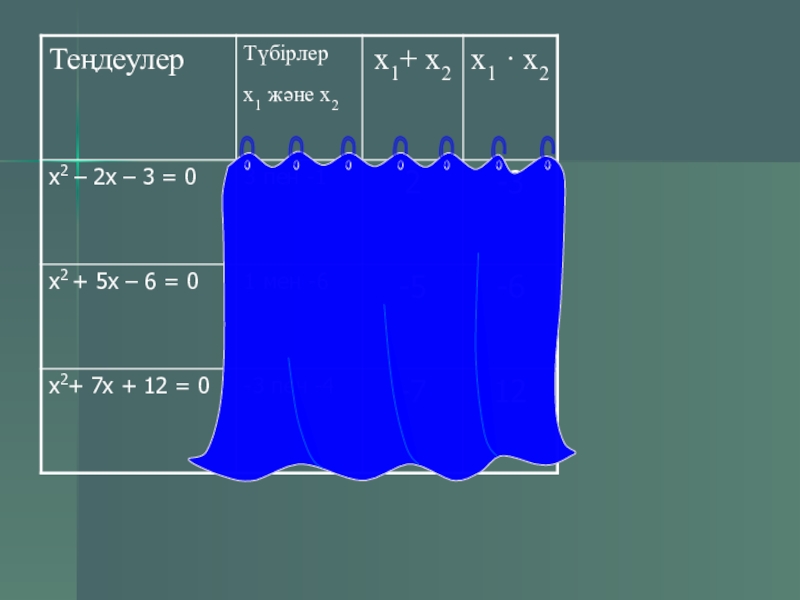
- 14. Виет теоремасы x2 + pх +
- 15. Слайд 15
- 16. Теңдеулердің коэффициенттерін атаңдар және қосындысын табыңдар 1)
- 17. Теңдеу
- 18. Тест сұрақтары:Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін
- 19. Жауабы тест:8; 15x2 + 8х + 7
- 20. Өздік жұмысы1 нұсқа2 нұсқа
- 21. Жауабы:1 нұсқа.1. 1 и -161 и -1,51
- 22. Молодец !
- 23. Қате
- 24. Рахмет
Өзінді тексер!
Слайд 1Квадрат
теңдеулер
Математика пәнінің мұғалімі: Жунусова К.К.
Алгебра 8 сынып
Семей қаласы «№19 жалпы
Слайд 3Квадрат теңдеу
ах2 + вх + с = 0 (а≠0) түріндегі
теңдеуді
квадрат теңдеу деп
атайды. Мұнда а,в,с – берілген
сандар, ал х - айнымалы
атайды. Мұнда а,в,с – берілген
сандар, ал х - айнымалы
Слайд 4Квадрат теңдеудің
дискриминанты
ах2 + bх + с =
0 теңдеудің дискриминанты деп b2 – 4ac өрнегі аталады.
D әрпімен белгіленеді, D= b2 – 4ac.
Бұл жерде үш жағдайды қарастырамыз:
D > 0
D = 0
D < 0
Бұл жерде үш жағдайды қарастырамыз:
D > 0
D = 0
D < 0
Слайд 13
Бұл теореманы бірінші дәлелдеген
француз математигі Француа Виет
(1540-1603) болғандықтан, соның атымен аталады.
Кейбір есептерді шешкенде Виет теоремасына кері теореманы қолданады.
Теорема (кері теорема). Егер сандары үшін шарттары орындалса, онда сандары теңдеуінің түбірлері болады.
француз математигі Француа Виет
(1540-1603) болғандықтан, соның атымен аталады.
Кейбір есептерді шешкенде Виет теоремасына кері теореманы қолданады.
Теорема (кері теорема). Егер сандары үшін шарттары орындалса, онда сандары теңдеуінің түбірлері болады.
Слайд 16Теңдеулердің коэффициенттерін
атаңдар және қосындысын табыңдар
1) х2-5х+1=0;
2) 9х2-6х+10=0;
3) х2+2х-2=0;
4) х2-3х-1=0;
5) х2+2х-3=0;
6) 5х2-8х+3=0;
Коэффициенттердың қосындысы
1-5+1=-3.
9-6+10=13.
1+2-2=1.
1-3-1=-3.
1+2-3=0.
5-8+3=0.
Слайд 17 Теңдеу Коэффициенттердың
Түбірлері
қосындысы
х2+4х-5=0; 0 1; -5 3х2+3х-6=0; 0 1; -2 5х2-8х+3=0; 0 1; 0,6 -7х2+2х+5=0; 0 1; -5/7 -2х2-5х+7=0 0 1; -3,5
қосындысы
х2+4х-5=0; 0 1; -5 3х2+3х-6=0; 0 1; -2 5х2-8х+3=0; 0 1; 0,6 -7х2+2х+5=0; 0 1; -5/7 -2х2-5х+7=0 0 1; -3,5
Слайд 18Тест сұрақтары:
Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:
А) 8; 15 В) -8; 15 С) 8; -15 D) -8; -15 Е) 5; -18
2. Түбірлері болатын теңдеуді жазыңдар:
А) В) С)
D) Е)
теңдеуінің бір түбірі 7-ге тең. Екінші түбірін және
р-ны табыңдар.
А) 2; 5 В) -2; 5 С) -5; -2 D) 2; -5 Е) 5; -1.
4. Теңдеудің түбірлерін табыңдар:
А) 11; 10 В) -1; 10 С) 1; 10 D) 1; -10 Е) -1; -10
5. Келтірілген квадраттық теңдеуді көрсет:
А) В) С)
D) Е)