и методика её построения.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математической логике Формулы алгебры логики. Таблицы истинности
Содержание
- 1. Презентация по математической логике Формулы алгебры логики. Таблицы истинности
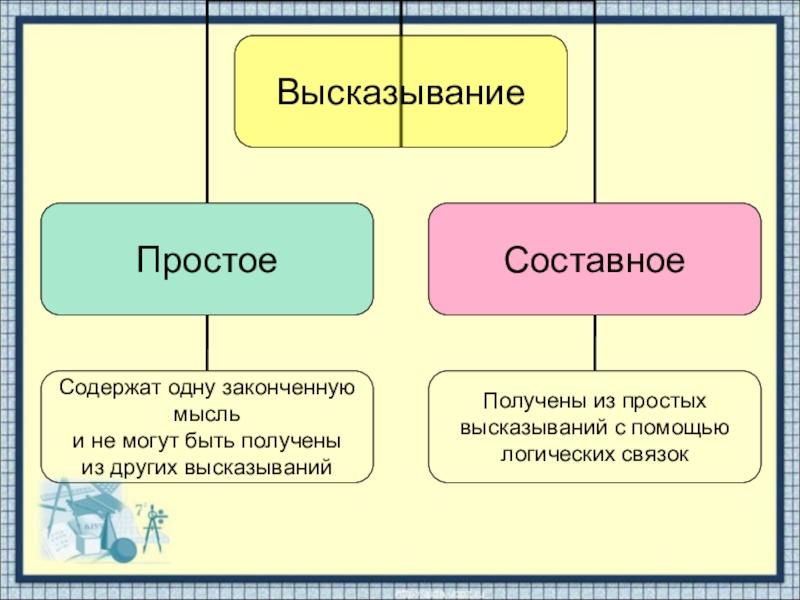
- 2. Высказыванием называется утверждение, которое является истинным или ложным *
- 3. Обозначение - Функция истинности
- 4. Слайд 4
- 5. Основные логические операцииДизъюнкция – переход к составному
- 6. Основные логические операцииКонъюнкция – переход к составному
- 7. Основные логические операцииОтрицание (инверсия) – переход к
- 8. Основные логические операцииИмпликация – переход к составному
- 9. Основные логические операцииЭквиваленция – переход к составному
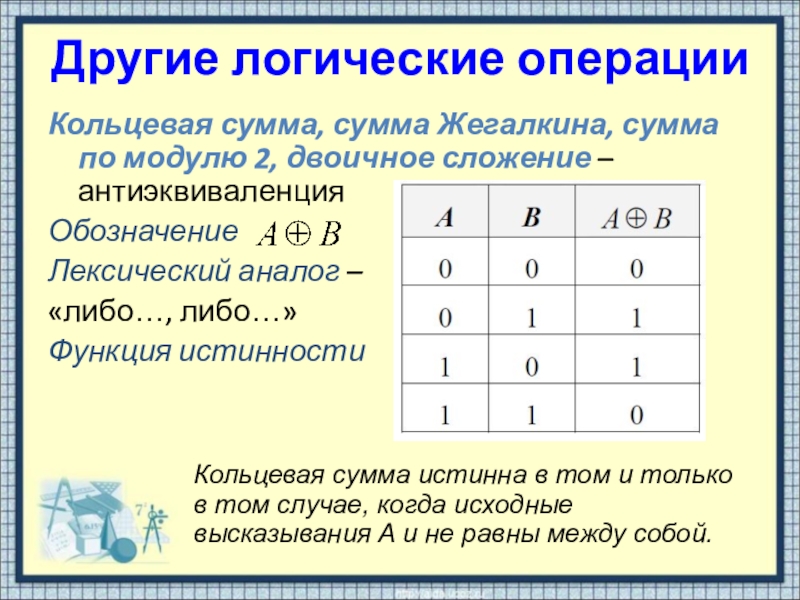
- 10. Другие логические операцииКольцевая сумма, сумма Жегалкина, сумма
- 11. Другие логические операцииСтрелка Пирса – антидизъюнкцияОбозначение Лексический
- 12. Другие логические операцииШтрих Шеффера – антиконъюнкцияОбозначение Лексический
- 13. Приоритет операцийВыполняются действия в скобкахВнешние скобки не пишутсяОстальные операции выполняются согласно схеме
- 14. Пример234156123456
- 15. Формула алгебры логикиотдельно стоящая буква A, B,
- 16. Виды формул АЛФормула называется тавтологией, если она
- 17. Построение таблицы истинностиПодсчитать количество переменных в формуле
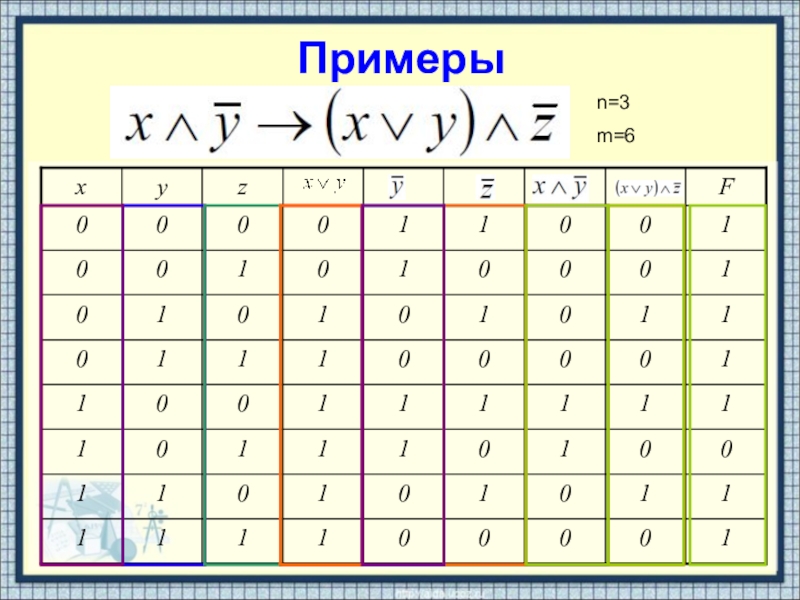
- 18. Примерыn=3m=6
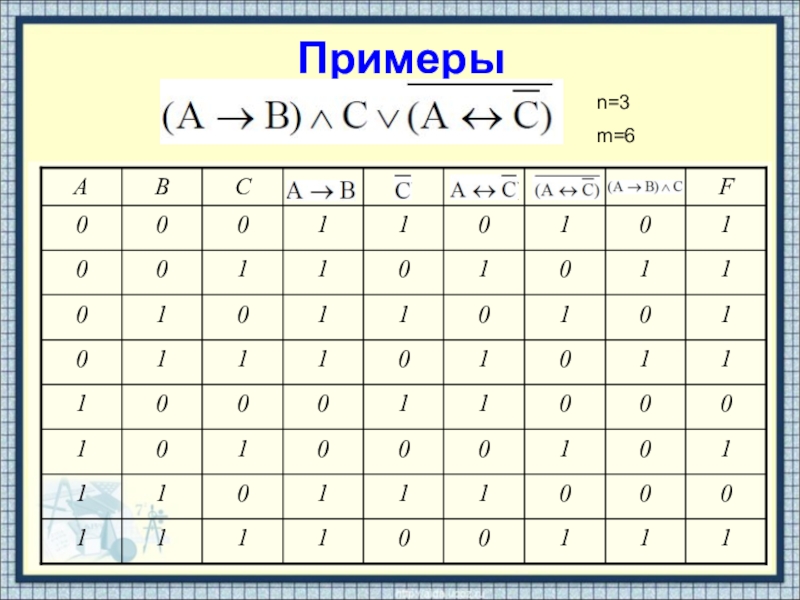
- 19. Примерыn=3m=6
- 20. Решить самостоятельно1.2.3.4.
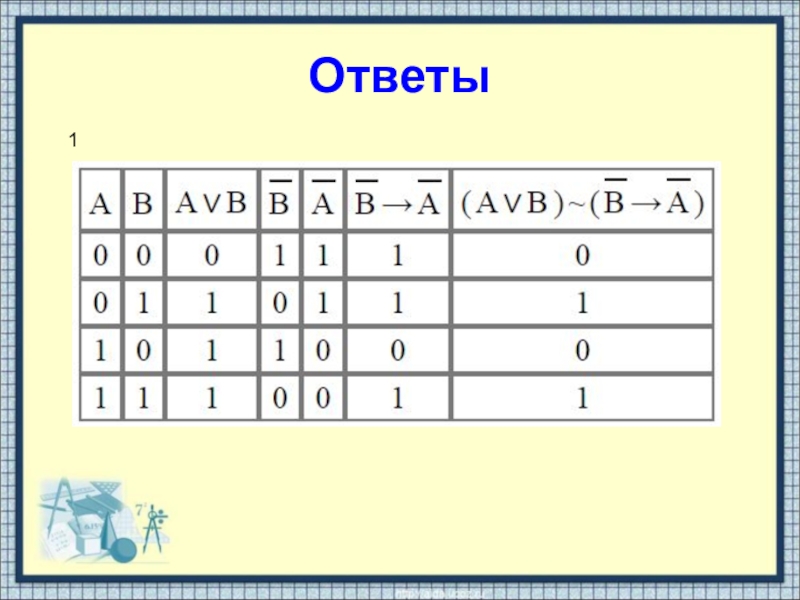
- 21. Ответы1
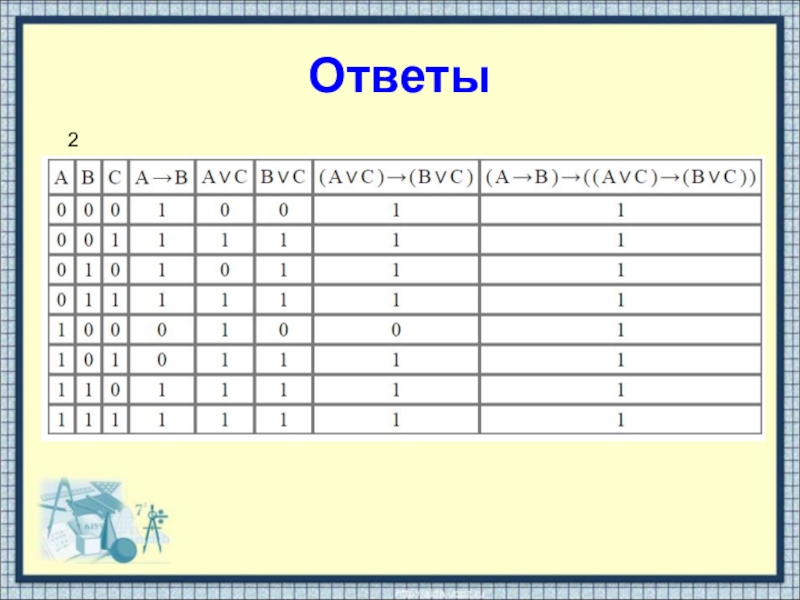
- 22. Ответы2
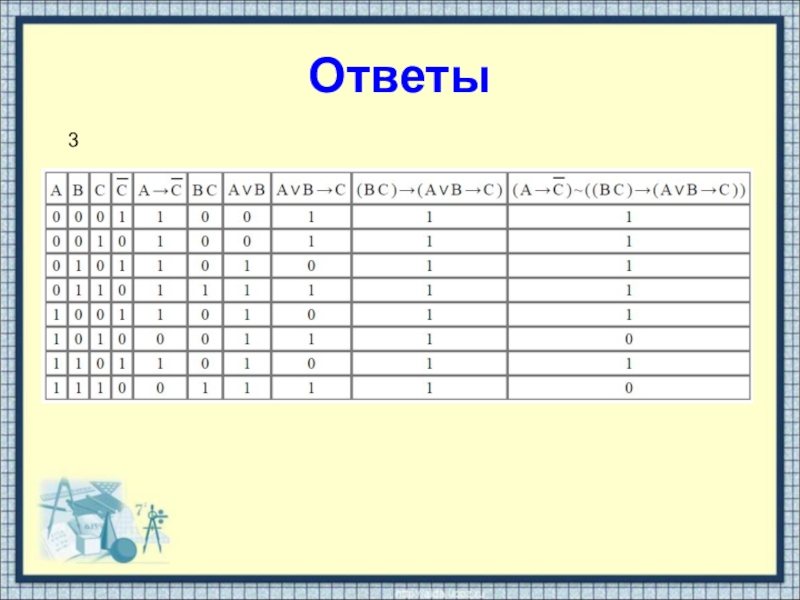
- 23. Ответы3
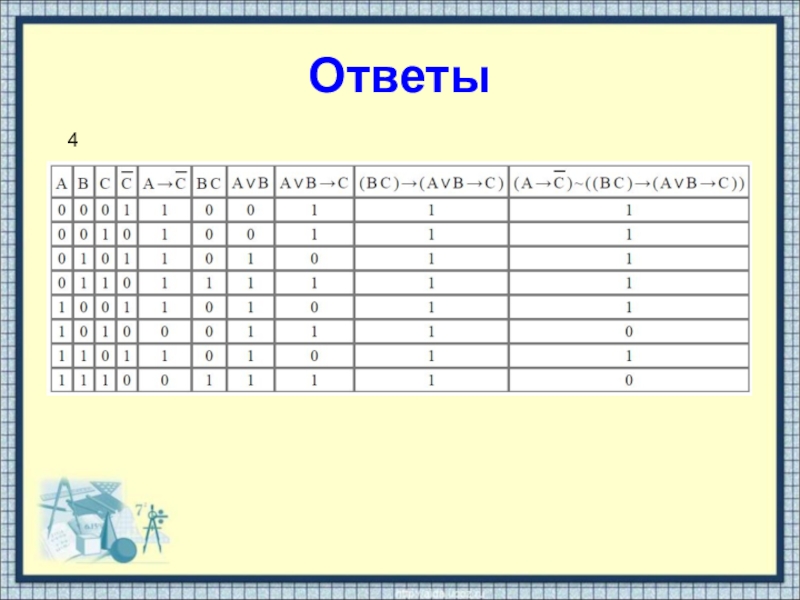
- 24. Ответы4
Высказыванием называется утверждение, которое является истинным или ложным *
Слайд 1Формулы алгебры логики
Понятие высказывания.
Основные логические операции. Формулы логики. Таблица истинности
Слайд 5Основные логические операции
Дизъюнкция – переход к составному высказыванию, которое является истинным,
если истинно хотя бы одно из высказываний А и В
Обозначение A∨B
Лексический аналог - «или», «либо», ...
Функция истинности
Обозначение A∨B
Лексический аналог - «или», «либо», ...
Функция истинности
Слайд 6Основные логические операции
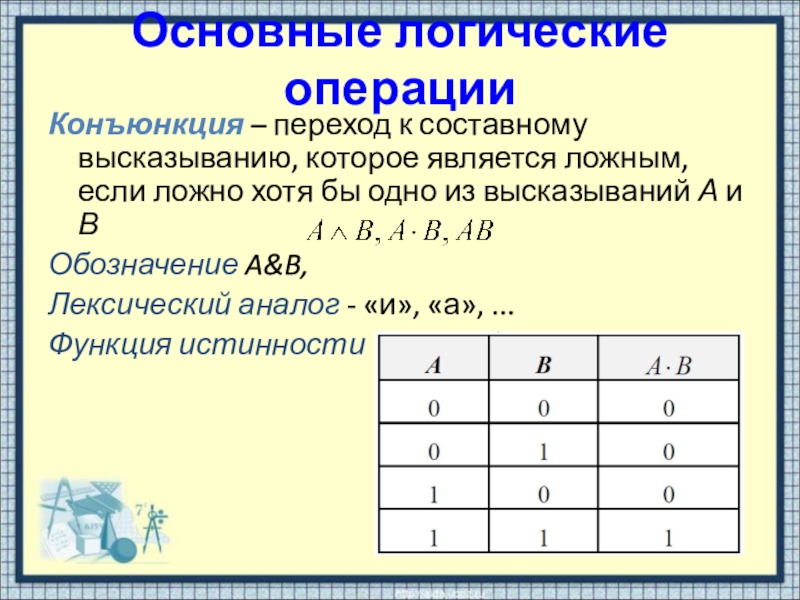
Конъюнкция – переход к составному высказыванию, которое является ложным,
если ложно хотя бы одно из высказываний А и В
Обозначение A&B,
Лексический аналог - «и», «а», ...
Функция истинности
Обозначение A&B,
Лексический аналог - «и», «а», ...
Функция истинности
Слайд 7Основные логические операции
Отрицание (инверсия) – переход к новому высказыванию, которое является
истинным, если высказывание А ложно и ложно в противном случае.
Обозначение
Лексический аналог - «не»
Функция истинности
Обозначение
Лексический аналог - «не»
Функция истинности
Слайд 8Основные логические операции
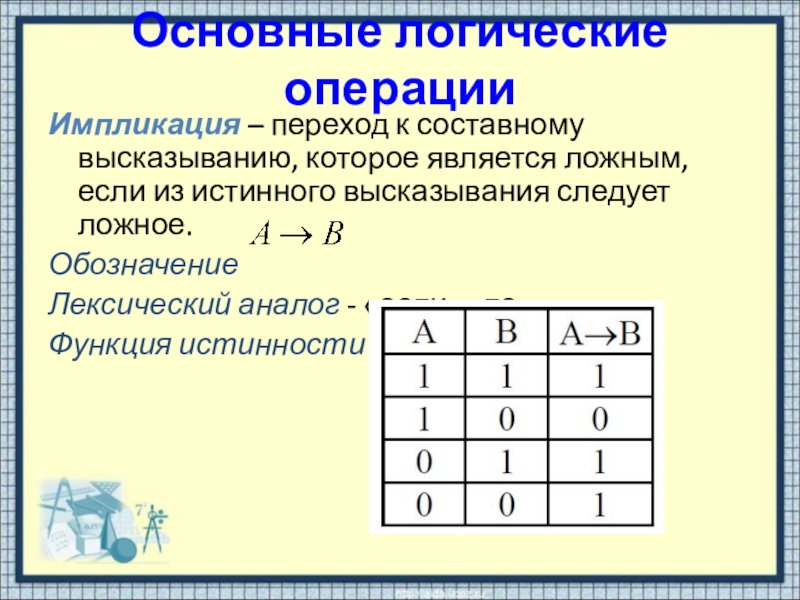
Импликация – переход к составному высказыванию, которое является ложным,
если из истинного высказывания следует ложное.
Обозначение
Лексический аналог - «если..., то...»
Функция истинности
Обозначение
Лексический аналог - «если..., то...»
Функция истинности
Слайд 9Основные логические операции
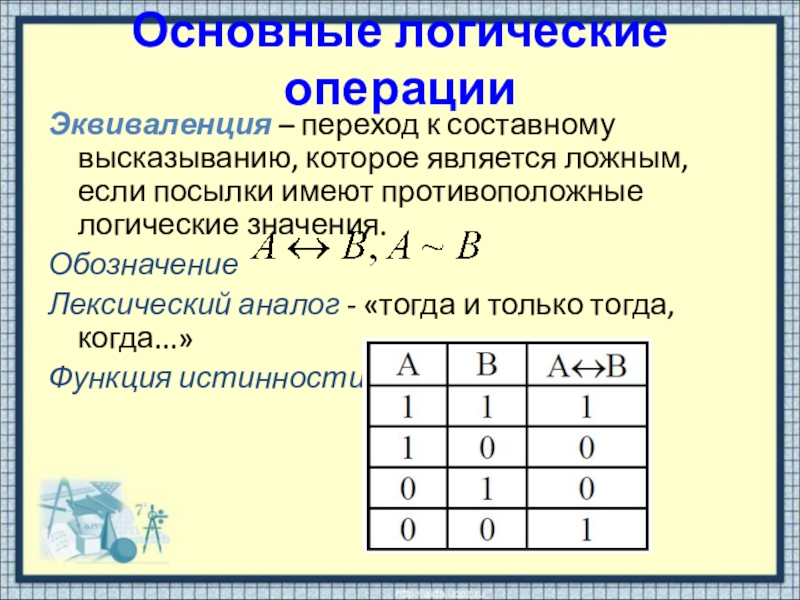
Эквиваленция – переход к составному высказыванию, которое является ложным,
если посылки имеют противоположные логические значения.
Обозначение
Лексический аналог - «тогда и только тогда, когда...»
Функция истинности
Обозначение
Лексический аналог - «тогда и только тогда, когда...»
Функция истинности
Слайд 10Другие логические операции
Кольцевая сумма, сумма Жегалкина, сумма по модулю 2, двоичное
сложение – антиэквиваленция
Обозначение
Лексический аналог –
«либо…, либо…»
Функция истинности
Обозначение
Лексический аналог –
«либо…, либо…»
Функция истинности
Кольцевая сумма истинна в том и только в том случае, когда исходные высказывания A и не равны между собой.
Слайд 11Другие логические операции
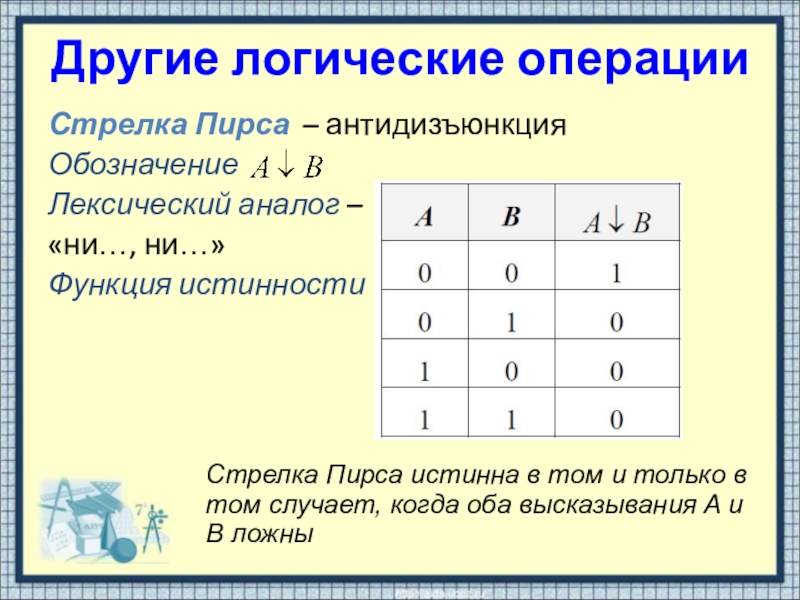
Стрелка Пирса – антидизъюнкция
Обозначение
Лексический аналог –
«ни…, ни…»
Функция
истинности
Стрелка Пирса истинна в том и только в том случает, когда оба высказывания A и B ложны
Слайд 12Другие логические операции
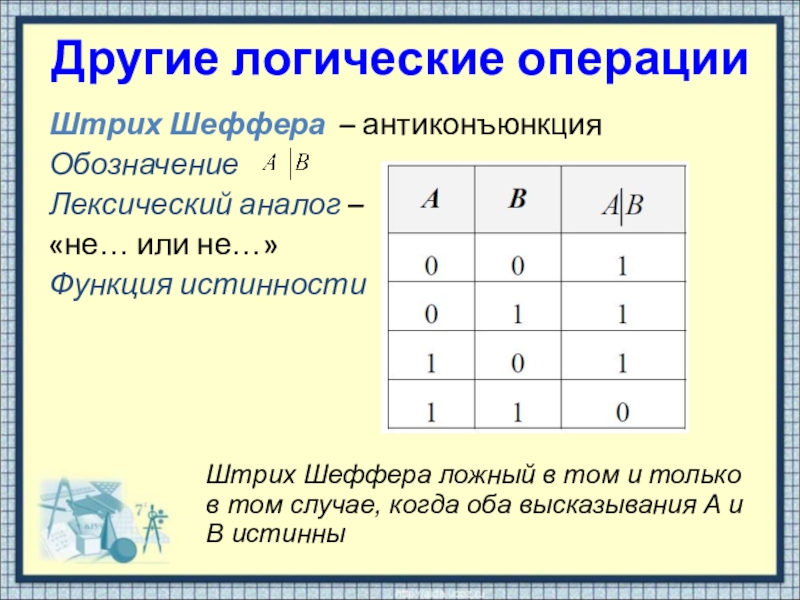
Штрих Шеффера – антиконъюнкция
Обозначение
Лексический аналог –
«не… или
не…»
Функция истинности
Функция истинности
Штрих Шеффера ложный в том и только в том случае, когда оба высказывания A и B истинны
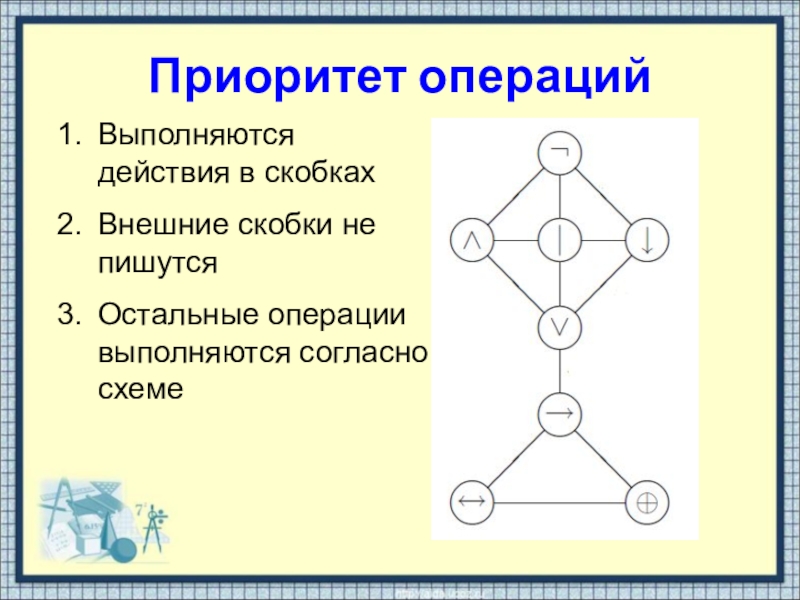
Слайд 13Приоритет операций
Выполняются действия в скобках
Внешние скобки не пишутся
Остальные операции выполняются согласно
схеме
Слайд 15Формула алгебры логики
отдельно стоящая буква A, B, C, ... , X,
Y, Z ... – формула
если А, В - формулы, то формулами являются и А, В, А∧В, А∨В, А→В, А↔В, А I В, А ↓В, А В.
других формул нет
если А, В - формулы, то формулами являются и А, В, А∧В, А∨В, А→В, А↔В, А I В, А ↓В, А В.
других формул нет
Слайд 16Виды формул АЛ
Формула называется тавтологией, если она принимает только истинные значения
при любых значениях букв. Другими словами, тавтология – это тождественно истинная формула.
Формула называется противоречивой, если она принимает только ложные значения при любых значениях букв. Другими словами, противоречивая – это тождественно ложная формула.
Формула называется выполнимой, если она принимает истинное значение хотя бы на одном наборе переменных.
Формула называется опровержимой, если она принимает ложное значение хотя бы на одном наборе переменных.
Формула называется противоречивой, если она принимает только ложные значения при любых значениях букв. Другими словами, противоречивая – это тождественно ложная формула.
Формула называется выполнимой, если она принимает истинное значение хотя бы на одном наборе переменных.
Формула называется опровержимой, если она принимает ложное значение хотя бы на одном наборе переменных.
Слайд 17Построение таблицы истинности
Подсчитать количество переменных в формуле n.
Определить количество строк в
таблице –
Подсчитать количество операций в формуле и определить количество столбцов m + n.
Записать названия столбцов с учетом последовательности выполнения операций.
Заполнить столбцы переменных наборами от 00...0 до 11...1 в лексикографическом порядке, используя метод «последовательного деления столбцов пополам»
Заполнить таблицу по столбцам.
Подсчитать количество операций в формуле и определить количество столбцов m + n.
Записать названия столбцов с учетом последовательности выполнения операций.
Заполнить столбцы переменных наборами от 00...0 до 11...1 в лексикографическом порядке, используя метод «последовательного деления столбцов пополам»
Заполнить таблицу по столбцам.