- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Действия с векторами
Содержание
- 1. Презентация по геометрии на тему Действия с векторами
- 2. ОглавлениеСложение векторов.Вычитание векторов.Умножение вектора на число.
- 3. Сложение векторовПравило «Треугольника»Правило «Параллелограмма»Правило «Многоугольника»
- 4. Правило «Треугольника»Для сложения двух векторов A и
- 5. Правило «Треугольника»a + b = AB + BC = AC(для неколлинеарных векторов)baABC
- 6. Правило «Треугольника»a + b = AB + BC = AC(для коллинеарных векторов)ababABCCAB
- 7. Правило «Параллелограмма»Для сложения двух векторов A и
- 8. Правило «Параллелограмма»a + b = OA + OB = OCbaOABC
- 9. Правило «Многоугольника»От произвольной точки А плоскости или
- 10. Правило «Многоугольника»a + b + c +
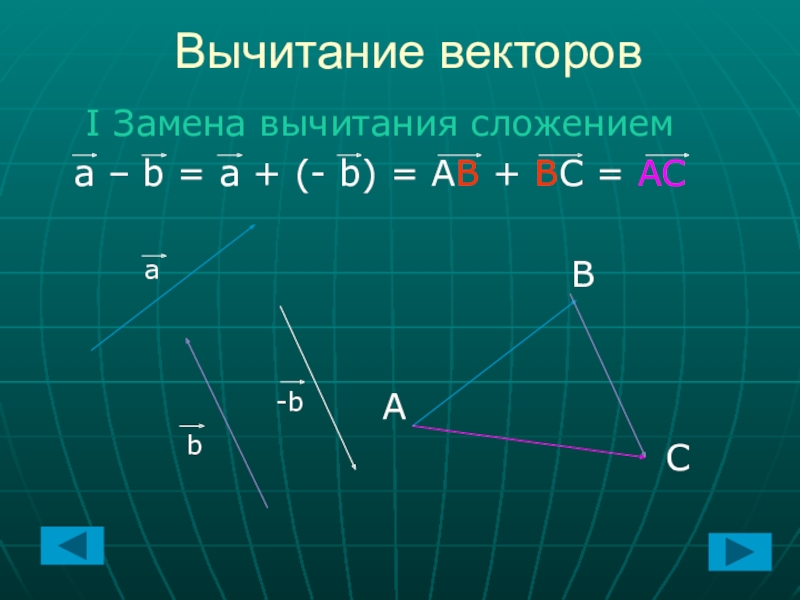
- 11. Вычитание векторовЧтобы из вектора а вычесть вектор
- 12. I Замена вычитания сложениемa – b =
- 13. Вычитание векторовII Вычитание векторов методом отложения их от одной точки.a– b =OA –OB = BAabOAB
- 14. Умножение вектора на числоУмножение вектора на число
- 15. Умножение вектора на числоk · a =
ОглавлениеСложение векторов.Вычитание векторов.Умножение вектора на число.
Слайд 4Правило «Треугольника»
Для сложения двух векторов A и B по правилу треугольника
оба эти векторы переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
Слайд 7Правило «Параллелограмма»
Для сложения двух векторов A и B по правилу параллелограмма
оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
Слайд 9Правило «Многоугольника»
От произвольной точки А плоскости или пространства откладывается вектор, равный
первому слагаемому, от его конца откладывается вектор, равный второму слагаемому, от его конца откладывается третье слагаемое, и так далее. Пусть точка B - это конец последнего отложенного вектора. Суммой всех этих векторов будет вектор AB .
Слайд 11Вычитание векторов
Чтобы из вектора а вычесть вектор b надо к вектору
а прибавить вектор, противоположный вектору b. Полученный в результате этой операции вектор с и будет являться разностью векторов а и b.
Слайд 13Вычитание векторов
II Вычитание векторов методом отложения их от одной точки.
a– b
=OA –OB = BA
a
b
O
A
B
Слайд 14Умножение вектора на число
Умножение вектора на число k соответствует растяжению вектора
в k раз при k > 1 или сжатию в раз при 0 < k < 1, при k = 1 вектор остается прежним (для отрицательных k еще изменяется направление на противоположное). Если произвольный вектор умножить на ноль, то получим нулевой вектор. Произведение нулевого вектора и произвольного числа есть нулевой вектор. К примеру, при умножении вектора a на число 2 нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора b на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное.
Слайд 15Умножение вектора на число
k · a = b ⬄ 1.|k| ·|a|
= |b|
2.Если k ≥ 0, то b a,
если k < 0, то b a.
2.Если k ≥ 0, то b a,
если k < 0, то b a.
a
3a
- 2a
-0,5a