- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Кусочная функция
Содержание
Слайд 1Кусочно
непрерывная
функция
Построение графика,
чтения свойств
Попкова Т.Г. МБОУ СОШ №2 г.Горячий
Слайд 2Функция y = f(x).
y = f(x) - зависимость y от x
1)Область определения функции – допустимые
значения аргумента (х).
x – независимая переменная (аргумент)
y – зависимая переменная (функция)
f – правило зависимости (уравнение, график и т.д.)
ширина по Ох
2)Множество значений функции – соответствующие
значения функции (y).
высота по Оу
D(y)
E(y)
Для каждого значения х – единственное значение у.
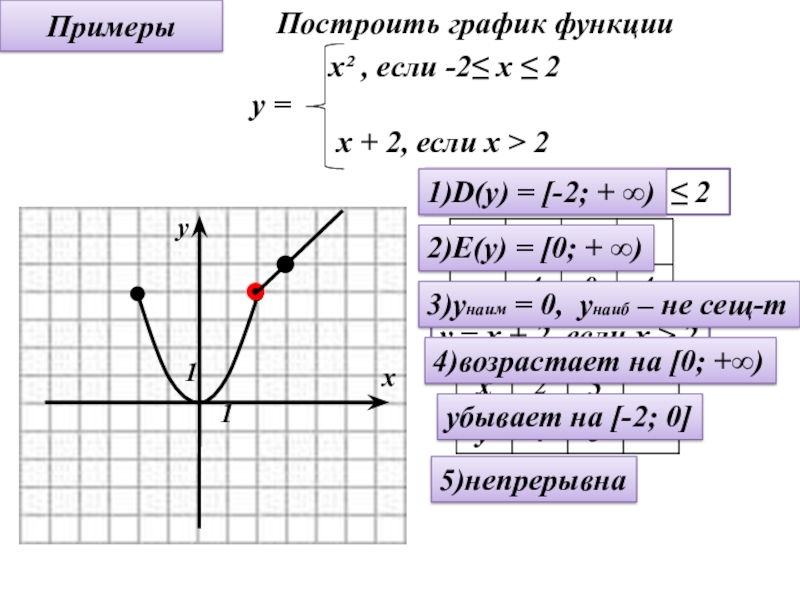
Слайд 3Примеры
y = x² , если -2≤ x ≤ 2
y =
Построить график функции
1)D(y) = [-2; + ∞)
2)E(y) = [0; + ∞)
3)yнаим = 0, yнаиб – не сещ-т
4)возрастает на [0; +∞)
убывает на [-2; 0]
5)непрерывна
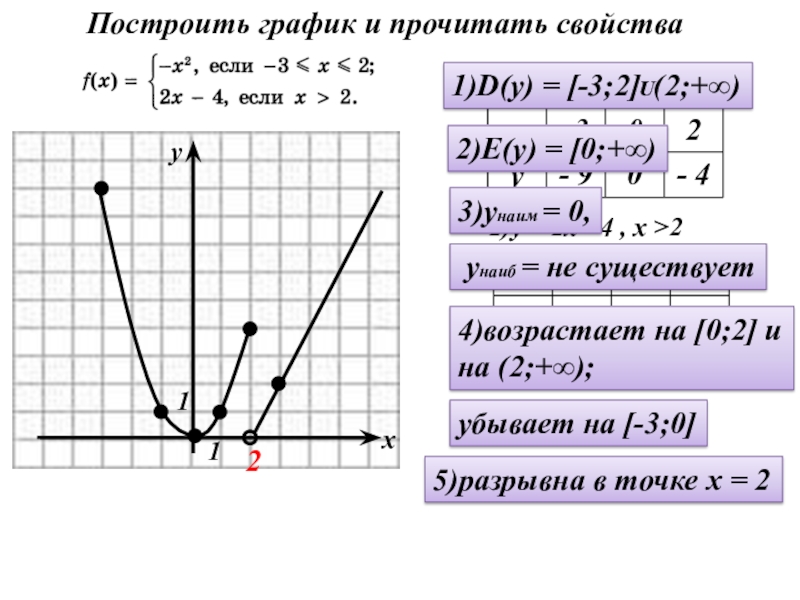
Слайд 41)у = - х² , - 3≤ х ≤ 2
2)у =
2
1)D(y) = [-3;2]ᴜ(2;+∞)
2)E(y) = [0;+∞)
3)yнаим = 0,
yнаиб = не существует
4)возрастает на [0;2] и
на (2;+∞);
убывает на [-3;0]
5)разрывна в точке х = 2
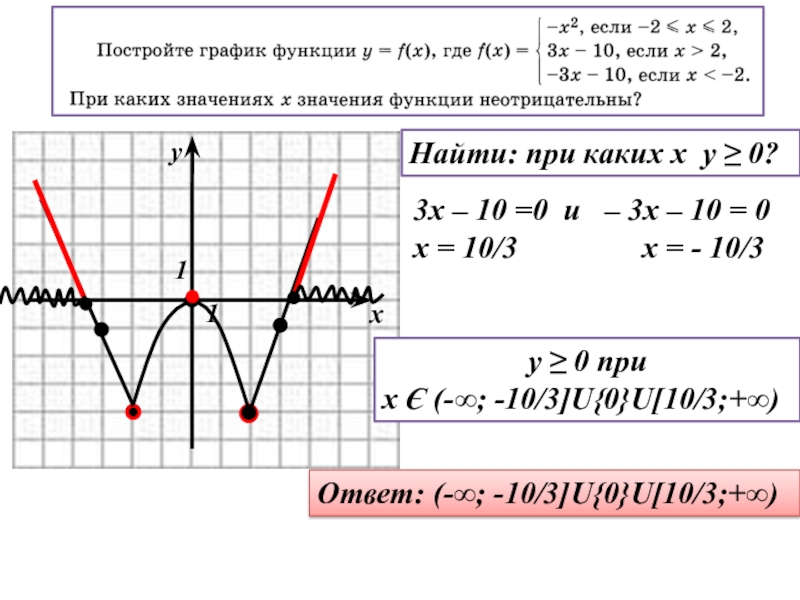
Слайд 6Найти: при каких x y ≥ 0?
3x – 10 =0
x = 10/3 x = - 10/3
y ≥ 0 при
x Є (-∞; -10/3]U{0}U[10/3;+∞)
Ответ: (-∞; -10/3]U{0}U[10/3;+∞)