Объем цилиндра»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад открытого урока по геометрии
Содержание
- 1. Презентация открытого урока по геометрии
- 2. «Математика – это …». «Математика – это доказательство».
- 3. ЗадачаЗадача 1. Классное помещение должно быть таким,
- 4. Что же такое объем:Объем-это метрическая единица измерения пространственной части стереометрического тела.
- 5. Рабочие листы1) Равные тела имеют________________ объёмы.2) Если
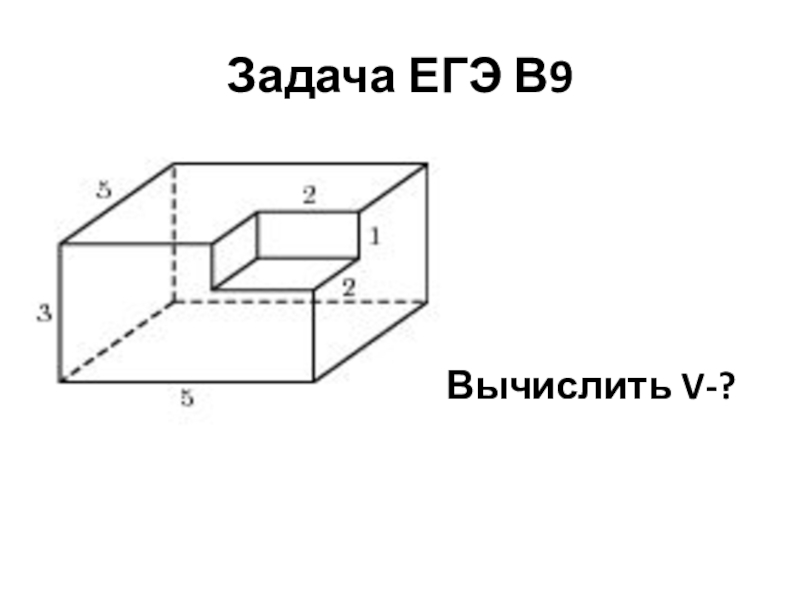
- 6. Задача ЕГЭ В9Вычислить V-?
- 7. Цилиндр: историяСлово "цилиндр" происходит от греческого kylindros, что означает "валик", "каток " …
- 8. Цилиндры из жизни
- 9. Объём цилиндраОбъём цилиндра равен произведению площади основания на высоту.
- 10. Объём цилиндра
- 11. Призма – многогранник, составленный из двух равных
- 12. Если боковые ребра призмы перпендикулярны к основаниям,
- 13. Теорема: Объем прямой призмы равен произведению площади
- 14. Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом
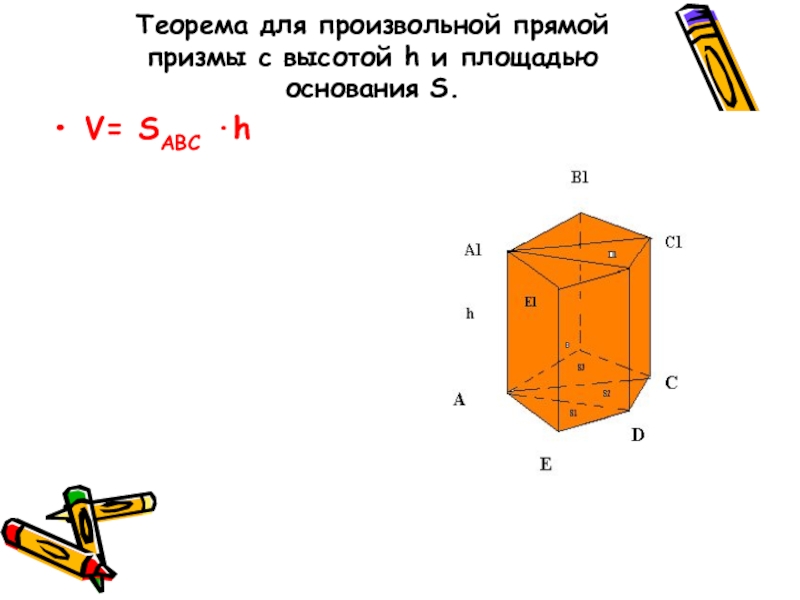
- 15. Теорема для произвольной прямой призмы с высотой h и площадью основания S.V= SABC ·h
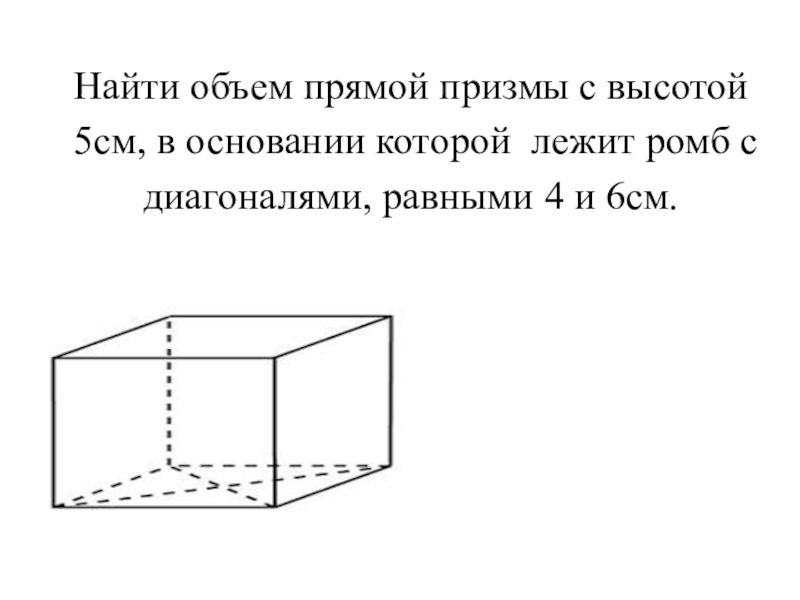
- 16. Найти объем прямой призмы с высотой
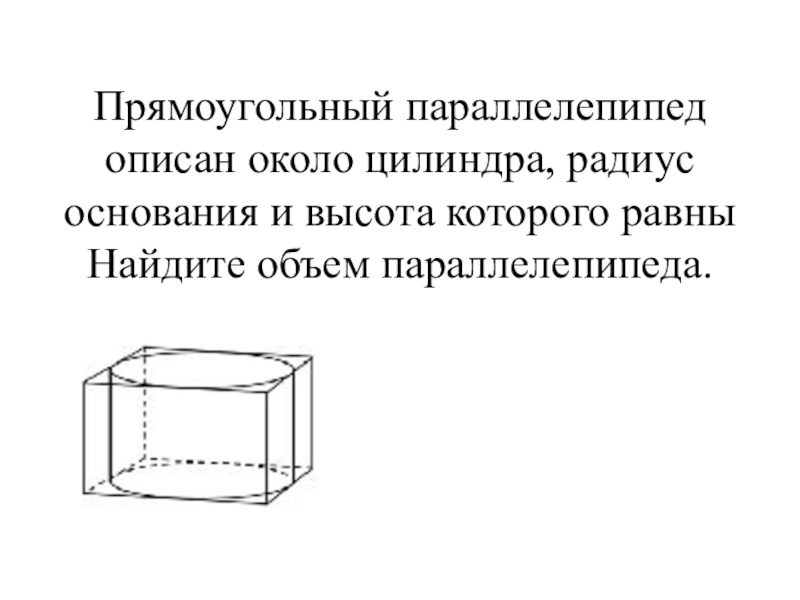
- 17. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны Найдите объем параллелепипеда.
- 18. Цилиндры-башниВодовзводная башня (Москва)Собственный дом архитектора К.Мельникова (Москва)Замок Сфорца (Милан)
- 19. Одна цилиндрическая кружка вдвое
- 20. Спасибо за урок!Быть здоровым – это быть
«Математика – это …». «Математика – это доказательство».
Слайд 3Задача
Задача 1. Классное помещение должно быть таким, чтобы на одного учащегося
приходилось не менее 6 м³ воздуха. Можно ли в кабинете математики , в котором мы находимся, заниматься с 18 учащимися, не нарушая санитарной нормы?
Н=3 м, а=6 м, в= 6 м.
Н=3 м, а=6 м, в= 6 м.
Слайд 4Что же такое объем:
Объем-это метрическая единица измерения пространственной части стереометрического тела.
Слайд 5Рабочие листы
1) Равные тела имеют________________ объёмы.
2) Если тело составлено из нескольких
тел, то его объём равен __________________ объёмов этих тел.
3) Объем прямоугольного параллелепипеда равен _____________________________ трех его измерений.
4) Объем прямоугольного параллелепипеда равен произведению __________________ ____________________на _______________.
5) Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению ____________________________________на _________ .
3) Объем прямоугольного параллелепипеда равен _____________________________ трех его измерений.
4) Объем прямоугольного параллелепипеда равен произведению __________________ ____________________на _______________.
5) Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению ____________________________________на _________ .
Слайд 7Цилиндр: история
Слово "цилиндр" происходит от греческого kylindros, что означает "валик", "каток
" …
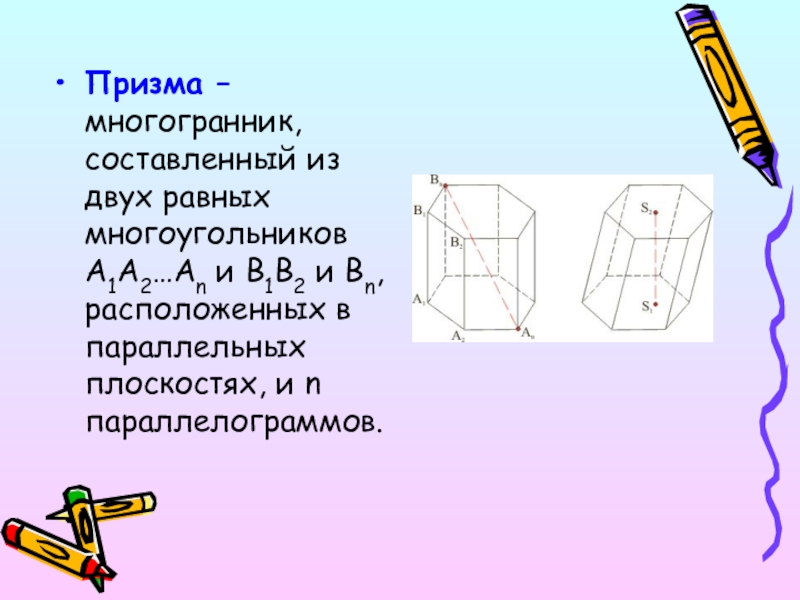
Слайд 11Призма – многогранник, составленный из двух равных многоугольников A1A2…An и B1B2
и Bn, расположенных в параллельных плоскостях, и n параллелограммов.
Слайд 12Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой.
Прямая
призма называется правильной, если её основания – правильные многоугольники.
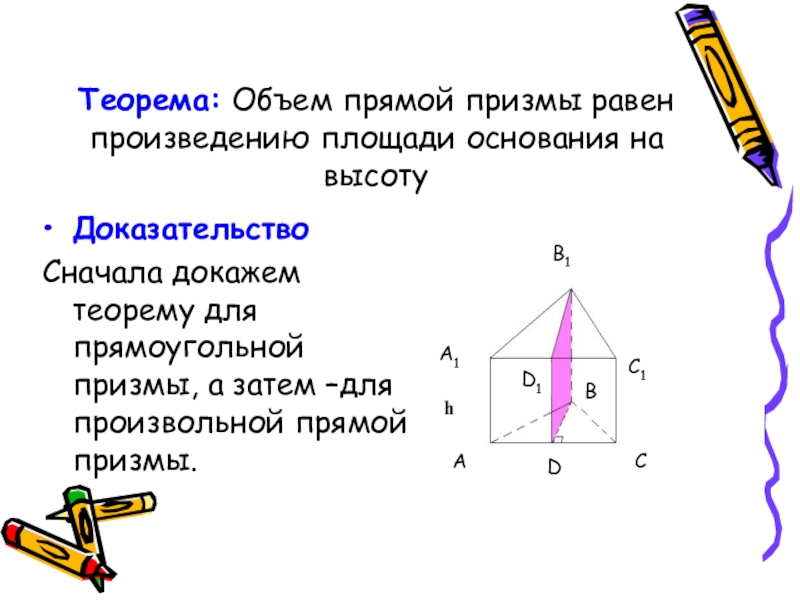
Слайд 13Теорема: Объем прямой призмы равен произведению площади основания на высоту
Доказательство
Сначала докажем
теорему для прямоугольной призмы, а затем –для произвольной прямой призмы.
В
D1
А1
В1
С1
А
C
D
Слайд 14Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом V и высотой h.
Проведем
такую высоту треугольника ABC (на рис. BD),которая разделяет этот треугольник на два треугольника.
Плоскость BB1D разделяет данную призму на 2 призмы, основаниями которых являются прямоугольные треугольники ABD и BDC.
Поэтому объемы V1 и V2 этих призм соответственно равны S ABD ·h и S BDC ·h. По свойству 2° объемов V=V1 +V2, т.е V=SABD ·h=(SABD+SBDC) · h.
Таким образом, V= SABC ·h.
Плоскость BB1D разделяет данную призму на 2 призмы, основаниями которых являются прямоугольные треугольники ABD и BDC.
Поэтому объемы V1 и V2 этих призм соответственно равны S ABD ·h и S BDC ·h. По свойству 2° объемов V=V1 +V2, т.е V=SABD ·h=(SABD+SBDC) · h.
Таким образом, V= SABC ·h.
V=SABC∙ h
В
D1
Слайд 16 Найти объем прямой призмы с высотой 5см, в основании которой лежит
ромб с диагоналями, равными 4 и 6см.
Слайд 17 Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны Найдите
объем параллелепипеда.
Слайд 18Цилиндры-башни
Водовзводная башня (Москва)
Собственный дом архитектора К.Мельникова (Москва)
Замок Сфорца (Милан)
Слайд 19 Одна цилиндрическая кружка вдвое выше второй, зато вторая в два раза шире.
Найдите отношение объема второй кружки к объему первой.
Слайд 20Спасибо за урок!
Быть здоровым – это быть счастливым,
Лишь здоровье ценится всегда.
Быть
здоровым – это быть красивым,
Молодым на долгие года.
Быть здоровым – это значит, Успевать в учебе и труде. Быть здоровым – это ведь удача, Всех людей, живущих на земле.
Но здоровье – ценность нашей жизни, Надо очень бережно хранить, Лишь его ни за какие деньги, Ни за что на свете не купить.
Быть здоровым – это значит, Успевать в учебе и труде. Быть здоровым – это ведь удача, Всех людей, живущих на земле.
Но здоровье – ценность нашей жизни, Надо очень бережно хранить, Лишь его ни за какие деньги, Ни за что на свете не купить.