«Нижнегорская школа-гимназия»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на семинар учителей математики Решение стереометрических задач из ЕГЭ
Содержание
- 1. Презентация на семинар учителей математики Решение стереометрических задач из ЕГЭ
- 2. Основные виды задач С2 Задача на доказательство
- 3. Основные методы решения стереометрических задач«метод построений»«векторный метод»
- 4. Справочный материал при подготовке учащихся к ЕГЭ
- 5. 2. Признак параллельности плоскостейЕсли две пересекающиеся прямые,
- 6. 3. Признак перпендикулярности прямой и плоскостиЕсли
- 7. 4. Теорема о трех перпендикулярахПрямая. Прямая, лежащая в
- 8. 5. Признак перпендикулярности плоскостейЕсли плоскость проходит через
- 9. Основные понятия, которые необходимы для «метода построений»
- 10. Задача №1 В правильной треугольной призме АВСА1В1С1
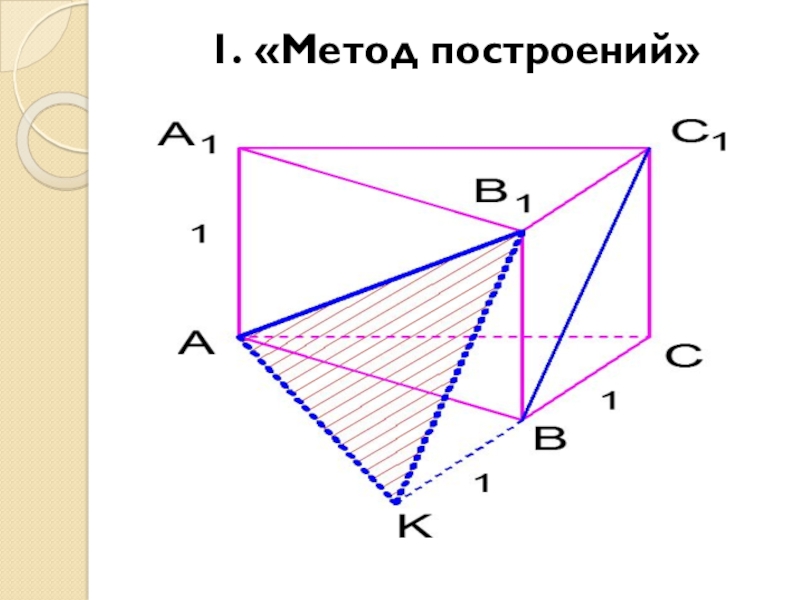
- 11. 1. «Метод построений»
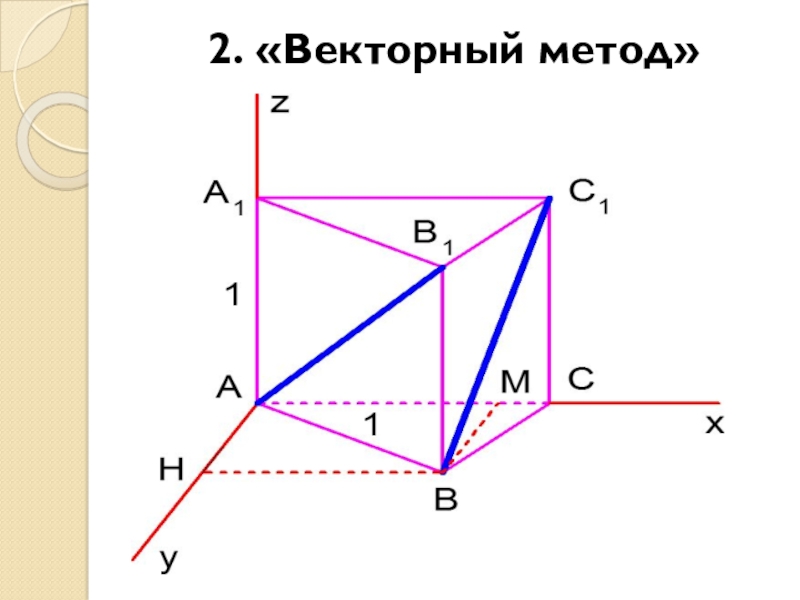
- 12. 2. «Векторный метод»
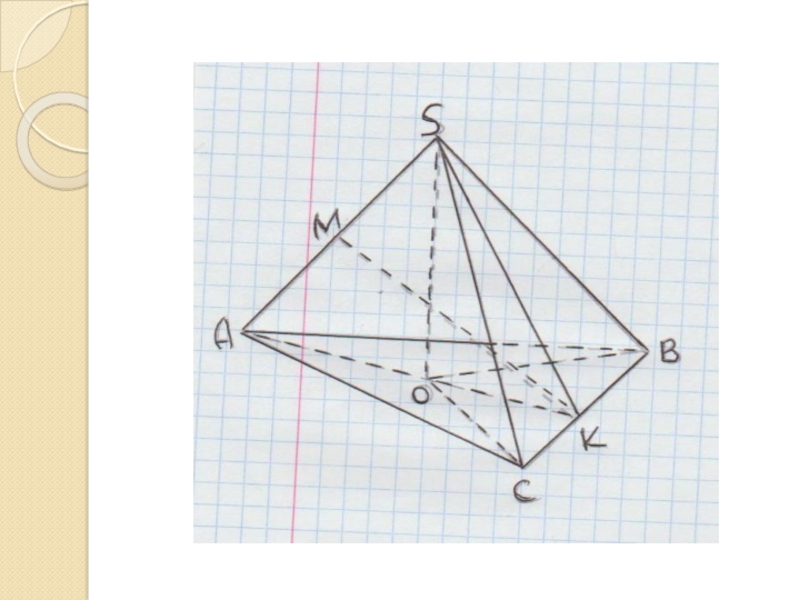
- 13. Задача № 2В пирамиде SABC известны длины
- 14. Слайд 14
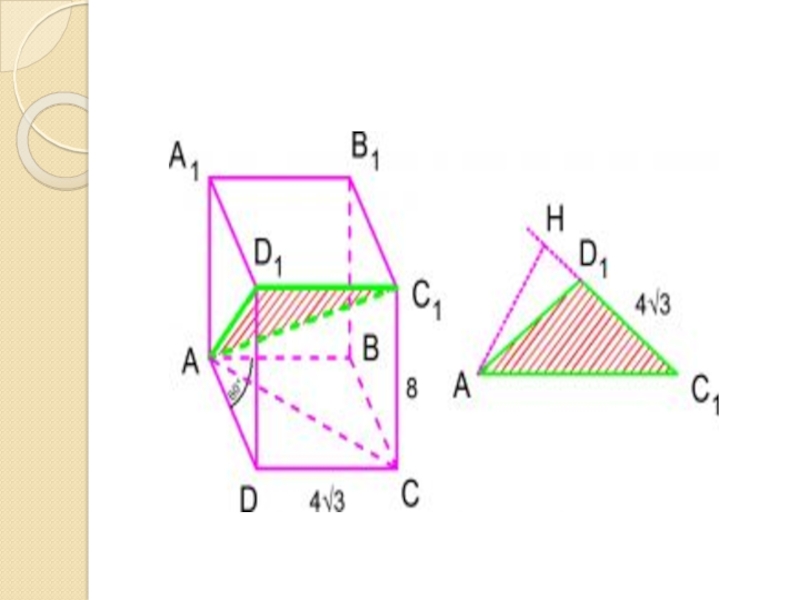
- 15. Задача №3. Основанием прямого параллелепипеда АВСDА1В1С1D1 является
- 16. Слайд 16
- 17. ВыводыРассмотрев различные подходы к решению задач, и
Основные виды задач С2 Задача на доказательство и вычисление.Угол между скрещивающимися прямыми. Угол между прямой и плоскостью. Угол между плоскостями. Расстояние от точки до прямой и до плоскости. Расстояние между прямыми и плоскостями. Сечения многогранников. Объёмы многогранников. Круглые тела: цилиндр, конус.
Слайд 2Основные виды задач С2
Задача на доказательство и вычисление.
Угол между скрещивающимися
прямыми.
Угол между прямой и плоскостью.
Угол между плоскостями.
Расстояние от точки до прямой и до плоскости.
Расстояние между прямыми и плоскостями.
Сечения многогранников.
Объёмы многогранников.
Круглые тела: цилиндр, конус.
Угол между прямой и плоскостью.
Угол между плоскостями.
Расстояние от точки до прямой и до плоскости.
Расстояние между прямыми и плоскостями.
Сечения многогранников.
Объёмы многогранников.
Круглые тела: цилиндр, конус.
Слайд 4Справочный материал при подготовке учащихся к ЕГЭ
1. Признак параллельности прямой и
плоскости
Если прямая не лежит в плоскости и параллельна какой-нибудь прямой, лежащей в данной плоскости, то она параллельна этой плоскости.
Если прямая не лежит в плоскости и параллельна какой-нибудь прямой, лежащей в данной плоскости, то она параллельна этой плоскости.
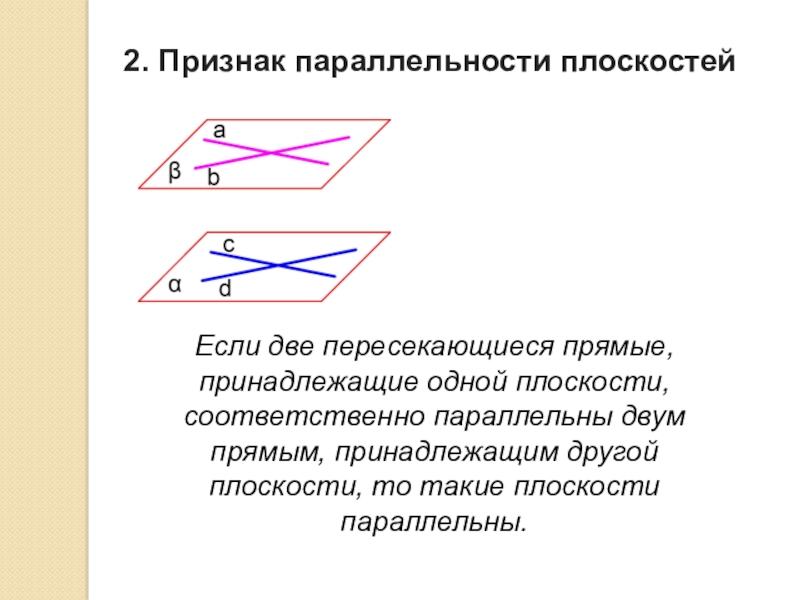
Слайд 52. Признак параллельности плоскостей
Если две пересекающиеся прямые, принадлежащие одной плоскости, соответственно
параллельны двум прямым, принадлежащим другой плоскости, то такие плоскости параллельны.
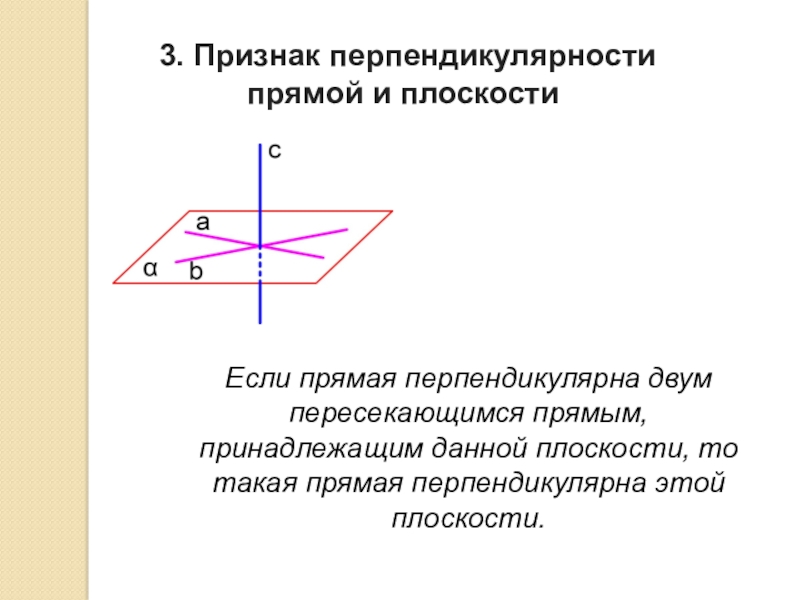
Слайд 6 3. Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна двум пересекающимся
прямым, принадлежащим данной плоскости, то такая прямая перпендикулярна этой плоскости.
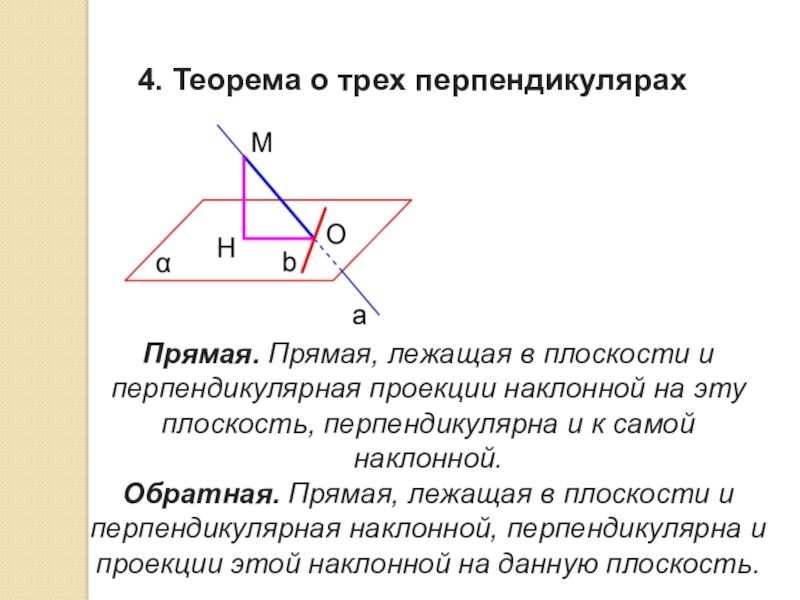
Слайд 74. Теорема о трех перпендикулярах
Прямая. Прямая, лежащая в плоскости и перпендикулярная проекции
наклонной на эту плоскость, перпендикулярна и к самой наклонной.
Обратная. Прямая, лежащая в плоскости и перпендикулярная наклонной, перпендикулярна и проекции этой наклонной на данную плоскость.
Обратная. Прямая, лежащая в плоскости и перпендикулярная наклонной, перпендикулярна и проекции этой наклонной на данную плоскость.
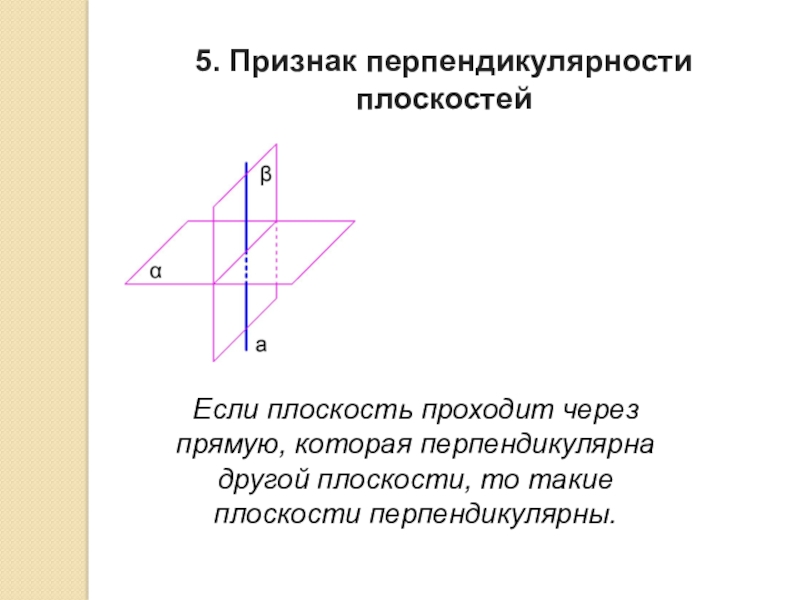
Слайд 85. Признак перпендикулярности плоскостей
Если плоскость проходит через прямую, которая перпендикулярна другой
плоскости, то такие плоскости перпендикулярны.
Слайд 10Задача №1 В правильной треугольной призме АВСА1В1С1 , все ребра которой
равны 1.
Найдите косинус угла между прямыми АВ1 и ВС1
Найдите косинус угла между прямыми АВ1 и ВС1
Слайд 13Задача № 2
В пирамиде SABC известны длины ребер AB=AC=SB= SC=10, BC=SA=12
Точка
К –середина ребра ВС.
а) Докажите, что плоскость SAК перпендикулярна плоскости АВС;
б) Найдите расстояние между прямыми SA и ВС.
а) Докажите, что плоскость SAК перпендикулярна плоскости АВС;
б) Найдите расстояние между прямыми SA и ВС.
Слайд 15Задача №3. Основанием прямого параллелепипеда АВСDА1В1С1D1 является ромб АВСD, сторона которого
равна , а угол ВАD равен 600.
Найдите расстояние от точки А до прямой С1D1, если известно, что боковое ребро данного параллелепипеда равно 8.
Найдите расстояние от точки А до прямой С1D1, если известно, что боковое ребро данного параллелепипеда равно 8.
Слайд 17Выводы
Рассмотрев различные подходы к решению задач, и проанализировав “эффект” от применения
этих способов решения можно сделать следующие выводы:
учащиеся выбирают метод решения задачи в соответствии со своими математическими предпочтениями, базирующимися на более прочных знаниях и уверенных навыках;
рекомендовать учащимся составлять план последовательных этапов для достижения результата;
используя основные теоремы стереометрии обосновывать все предпринимаемые шаги и вычисления;
Данный материал направлен на развитие пространственного мышления учащихся, на подготовку к сдаче ЕГЭ.
учащиеся выбирают метод решения задачи в соответствии со своими математическими предпочтениями, базирующимися на более прочных знаниях и уверенных навыках;
рекомендовать учащимся составлять план последовательных этапов для достижения результата;
используя основные теоремы стереометрии обосновывать все предпринимаемые шаги и вычисления;
Данный материал направлен на развитие пространственного мышления учащихся, на подготовку к сдаче ЕГЭ.