- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Корни натуральной степени из числа и их свойства
Содержание
- 1. Презентация Корни натуральной степени из числа и их свойства
- 2. Слайд 2
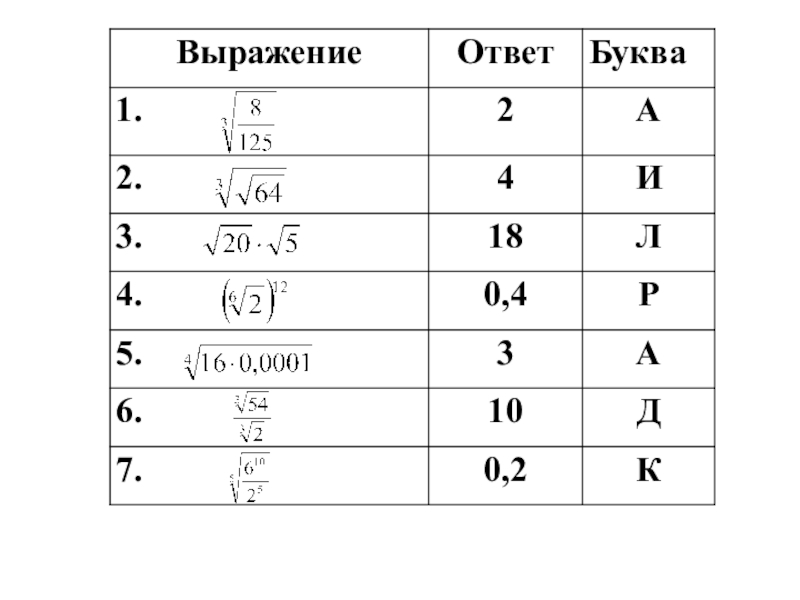
- 3. Устные упражнения1. Вычислить:
- 4. Устные упражнения2. Решите уравнение:
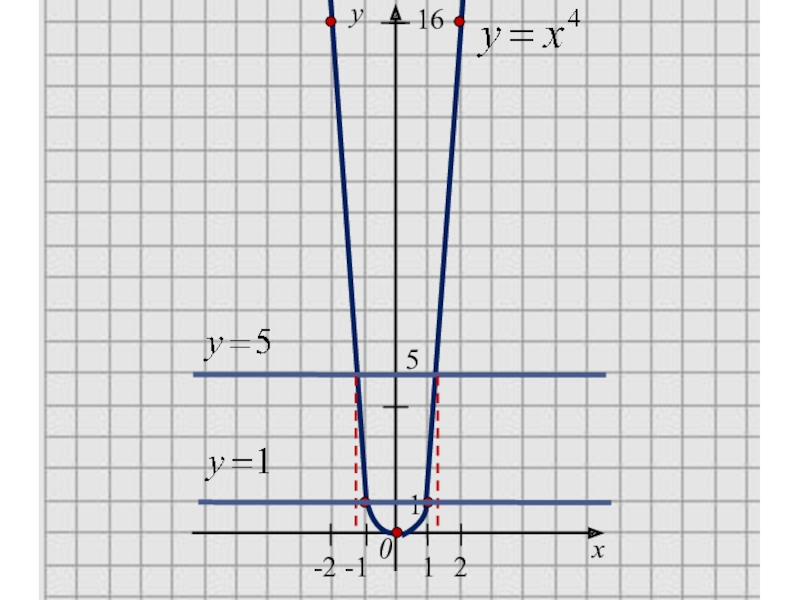
- 5. y0x16-1-21215
- 6. Слайд 6
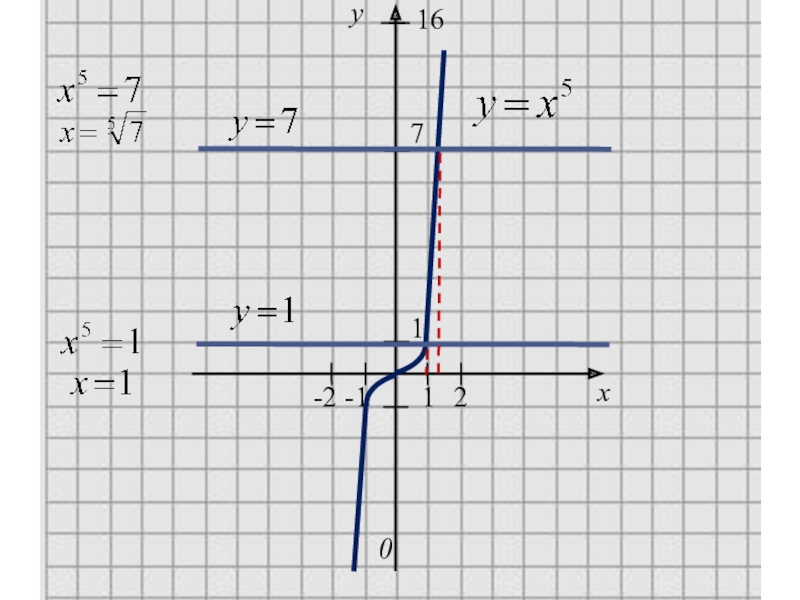
- 7. y0x16-1-21217
- 8. Тема учебного занятия:Корни натуральной степени из числа и их свойства
- 9. Арифметическим квадратным корнем из неотрицательного числа а называют такое неотрицательное число в, квадрат которого равен а.
- 10. Корнем n-й степени из неотрицательного числа a
- 11. Корень четной степени имеет смысл только для
- 12. Слайд 12
- 13. Свойство 1. Корень n-й степени из произведения
- 14. Свойство 2. Корень из дроби равен дроби от корней.
- 15. Решение примеров на применение свойств
- 16. Свойство 3. Для возведения корня в натуральную
- 17. Свойство 4. Для того, чтобы извлечь корень
- 18. Решение примеров на применение свойств
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Правила написания синквейна: 1-я строка – название
- 23. Критерии оценок:10 и более набранных баллов –
- 24. Домашнее задание :- доказать свойства 4 и
Устные упражнения1. Вычислить:
Слайд 9Арифметическим квадратным корнем из неотрицательного числа а называют такое неотрицательное число
в, квадрат которого равен а.
Слайд 10Корнем n-й степени из неотрицательного числа a называют такое неотрицательное
число, которое при возведении в степень n дает в результате число a.
Слайд 11Корень четной степени имеет смысл только
для неотрицательного подкоренного выражения;
корень
нечетной степени имеет смысл
для любого подкоренного выражения.
для любого подкоренного выражения.
Слайд 13Свойство 1. Корень n-й степени из произведения двух
неотрицательных чисел равен
произведению корней n-й степени из этих чисел:
Слайд 16Свойство 3. Для возведения корня в натуральную степень, достаточно возвести в
эту степень подкоренное выражение.
При k=3 получаем
Слайд 17Свойство 4. Для того, чтобы извлечь корень из корня,
достаточно перемножить
показатели корней.
Свойство 5. Если показатели корня и подкоренного
выражения умножить или разделить на одно и то же
натуральное число, то значение корня не изменится.
Замечание. Формула обобщается на случай любого четного показателя корня
Слайд 22Правила написания синквейна:
1-я строка – название синквейна - ОДНО слово,
обычно существительное, отражающее главную идею;
2-я строка – ДВА прилагательных, описывающих основную мысль;
3-я строка – ТРИ глагола, описывающие действия в рамках темы;
4-я строка – фраза на тему синквейна;
5-я строка – существительное, связанное с первым, отражающее сущность темы.
Слайд 23Критерии оценок:
10 и более набранных баллов – отметка «5»,
6 – 9
набранных баллов – отметка «4»,
4- 5 набранных баллов – отметка «3»,
менее 3-х набранных баллов – отметка «2»
4- 5 набранных баллов – отметка «3»,
менее 3-х набранных баллов – отметка «2»
Слайд 24Домашнее задание :
- доказать свойства 4 и 5;
- выполнить упражнения из
учебника [1] §5.1.(1) №5.1.,5.2;
- творческое задание на дополнительную отметку – составить кроссворд по теме «Степени и корни» с количеством слов от 12 до 20, желательно с использованием возможностей MS Office.
- творческое задание на дополнительную отметку – составить кроссворд по теме «Степени и корни» с количеством слов от 12 до 20, желательно с использованием возможностей MS Office.


















![Презентация Корни натуральной степени из числа и их свойства Домашнее задание :- доказать свойства 4 и 5;- выполнить упражнения из Домашнее задание :- доказать свойства 4 и 5;- выполнить упражнения из учебника [1] §5.1.(1) №5.1.,5.2;- творческое задание](/img/thumbs/3bc9013b849121368d1844cc86a5eb6a-800x.jpg)





