- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Обыкновенные дроби. Дробь как результат деления натуральных чисел
Содержание
- 1. Презентация к уроку по теме Обыкновенные дроби. Дробь как результат деления натуральных чисел
- 2. Вычислите удобным способом:88+40 – 823·16+16 ·7788+30+1267 ·60+33
- 3. Выполните действия и выразите делимое через неполное частное, делитель и остаток:75:948:17512:500370:185 75=9·8+3 48=17 ·2+14 512=500 ·1+12 370=185 ·2
- 4. Кусок проволоки длиной 1 м разрезали
- 5. Кусок проволоки длиной 1 м разрезали на
- 6. 1 3 Вспомните, как прочитать записанную дробь? Одна третья
- 7. одна 1 - числитель третья 3 - знаменательВспомните, как
- 8. Кусок проволоки длиной 1 м разрезали на
- 9. Частное от деления натуральных чисел можно записать
- 10. Частное от деления натуральных чисел m и
- 11. Как прочитать дробь: «эм энных»«эм деленное на n»(допускается сокращение эм на n).
- 12. Частное от деления натуральных чисел m и
- 13. Домашнее задание:П. 18 (стр.86). Записи в тетради.306 (в,г).314
- 14. Старинные задачи с дробями№ 1. Задача из
- 15. Старинные задачи с дробями№ 2. Задача из
- 16. Старинные задачи с дробями№ 3. Староиндийская задача
- 17. Старинные задачи с дробями№ 4. Задача армянского
- 18. Из истории дробейДроби появились в глубокой древности.
- 19. Из истории дробейОсобое место занимали дроби ½;
- 20. Из истории дробейЭти дроби (½; ¼; 1/8;
- 21. Из истории дробейДроби и действия с ними
- 22. Литература:1.И.И.Зубарева, А.Г.Мордкович «Математика 5» Мнемозина Москва 2004г.2.Н.Виленкин,
Слайд 1Орешко Светлана Анатольевна
МБОУ СОШ №46
г. Курск
Урок по теме:
Обыкновенные дроби
Дробь
Слайд 2Вычислите удобным способом:
88+40 – 8
23·16+16 ·77
88+30+12
67 ·60+33 ·60
79 ·22-69 ·22
= 88-8+40=120
=
= 88+12+30=130
= 60 ·(67+33)=6000
= 22 ·(79-69)=220
Слайд 3Выполните действия и выразите делимое через неполное частное, делитель и остаток:
75:9
48:17
512:500
370:185
75=9·8+3
48=17
512=500 ·1+12
370=185 ·2
Слайд 4Кусок проволоки длиной 1 м разрезали на 2 равные части. Какова
? ?
1 м
Вырази длину проволоки в дециметрах:
1 м= 10 дм.
Тогда
10 :2= 5 (дм).
Ответ: 5 дм длина одной части.
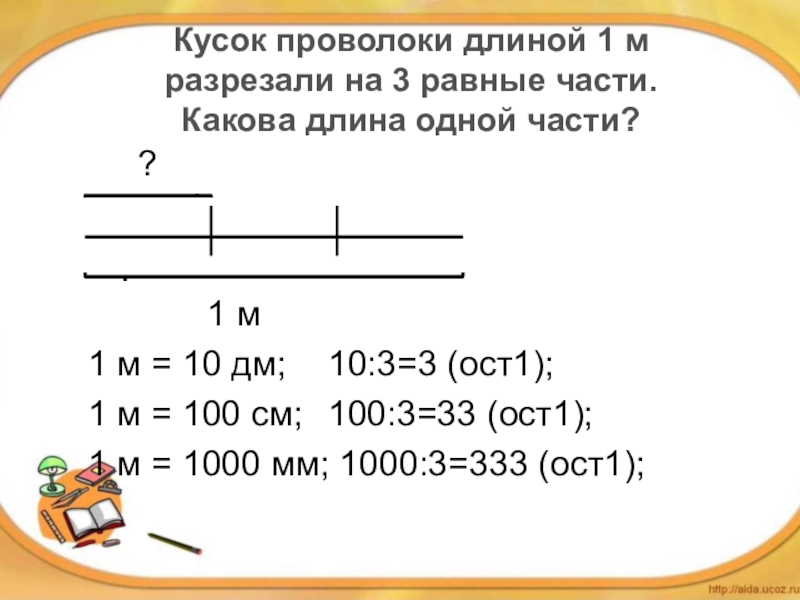
Слайд 5Кусок проволоки длиной 1 м разрезали на 3 равные части. Какова
?
1 м
1 м = 10 дм; 10:3=3 (ост1);
1 м = 100 см; 100:3=33 (ост1);
1 м = 1000 мм; 1000:3=333 (ост1);
Слайд 6 1
3
Вспомните, как прочитать записанную дробь?
Одна третья
Как называется число, стоящее над
Числитель
Как называется число, стоящее под чертой дроби?
Знаменатель
Что означает черта дроби?
Действие деления
Слайд 7 одна 1 - числитель
третья 3 - знаменатель
Вспомните, как прочитать записанную дробь?
Одна третья
Как
Числитель
Как называется число, стоящее под чертой дроби?
Знаменатель
Что означает черта дроби?
Действие деления
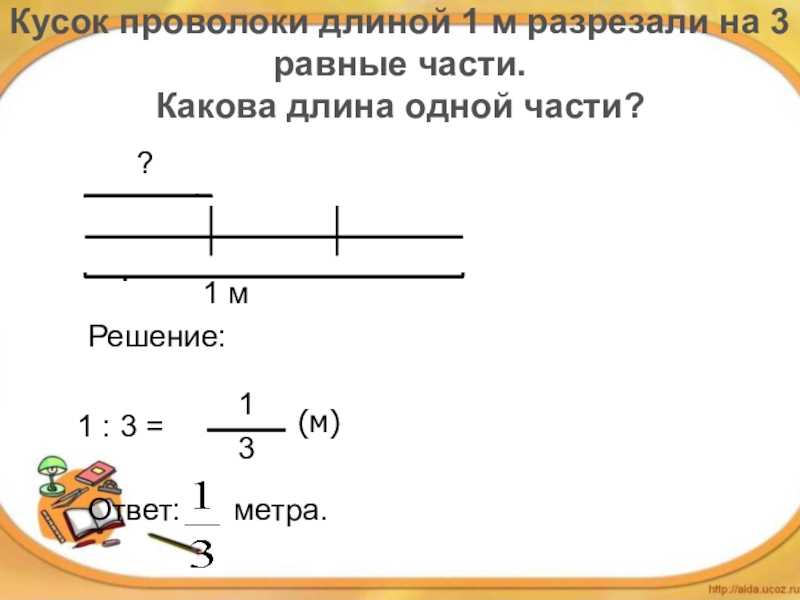
Слайд 8Кусок проволоки длиной 1 м разрезали на 3 равные части. Какова
?
1 м
Решение:
Ответ: метра.
(м)
Слайд 9Частное от деления натуральных чисел можно записать в виде дроби. Числитель дроби
Слайд 10Частное от деления натуральных чисел m и n можно записать
в
где числитель m –делимое, знаменатель n –делитель.
Слайд 12Частное от деления натуральных чисел m и n можно записать
в
где числитель m –делимое, а знаменатель n –делитель.
Слайд 14Старинные задачи с дробями
№ 1. Задача из «Арифметики» известного среднеазиатского математика
Мухаммеда ибн-Мусы аль Хорезми
(задача приведена в упрощенном варианте):
«Найти число, зная, что если отнять
от него одну треть и одну четверть, то получится 10»
Слайд 15Старинные задачи с дробями
№ 2. Задача из «Папируса Ахмеса»
(Египет, 1850
«Приходит пастух с 70 быками.
Его спрашивают:
- Сколько приводишь ты своего многочисленного стада?
Пастух отвечает:
Я привожу две трети от трети скота. Сочти».
Слайд 16Старинные задачи с дробями
№ 3. Староиндийская задача
(математика Сриддихары XI в.)
Есть
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда
И на ней третья часть поместилась.
Разность их ты найди,
Ее трижды сложи
И тех пчел на кутай посади,
Только две не нашли
Себе место нигде,
Все летали то взад, то вперед и везде
Ароматом цветов наслаждались.
Назови теперь мне
Подсчитавши в уме,
Сколько пчелок всего здесь собралось?
Слайд 17Старинные задачи с дробями
№ 4. Задача армянского ученого Анания Ширакаци
(VII
«Один купец прошел через 3 города, и взыскивали с него в первом городе и пошлину половину и треть имущества, и во втором городе половину и треть (с того, что осталось), и в третьем городе половину и треть (с того, что осталось). Когда он прибыл домой, у него осталось 11 денежков (денежных единиц). Итак, узнай, сколько всего денежков было вначале у купца».
Слайд 18Из истории дробей
Дроби появились в глубокой древности. Египтяне уже знали, как
Все остальные употреблявшиеся дроби непременно имели в числителе 1.
Если египтянину нужно было использовать другие отношения, он их представлял в виде суммы основных дробей.
Слайд 19Из истории дробей
Особое место занимали дроби ½; ¼; 1/8; 1/16 и
Дело в том, что в древности отдельной арифметической операцией полагали удвоение и деление пополам.
Слайд 20Из истории дробей
Эти дроби (½; ¼; 1/8; 1/16) сыграли определяющую роль
И сейчас в общепринятой нотной записи длинная нота – целая – делится на половинки, четверти, восьмые, шестнадцатые и тридцать вторые.
Таким образом, ритмический рисунок любого музыкального произведения, созданного европейской культурой, каким бы сложным он ни был, определяется двоичными дробями.
Слайд 21Из истории дробей
Дроби и действия с ними не всем легко даются.
Слайд 22Литература:
1.И.И.Зубарева, А.Г.Мордкович «Математика 5» Мнемозина Москва 2004г.
2.Н.Виленкин, В.Жохов, А.Чесноков, С.Швацбург «Математика
3. шаблон презентации http//aida.ucoz.ru
*