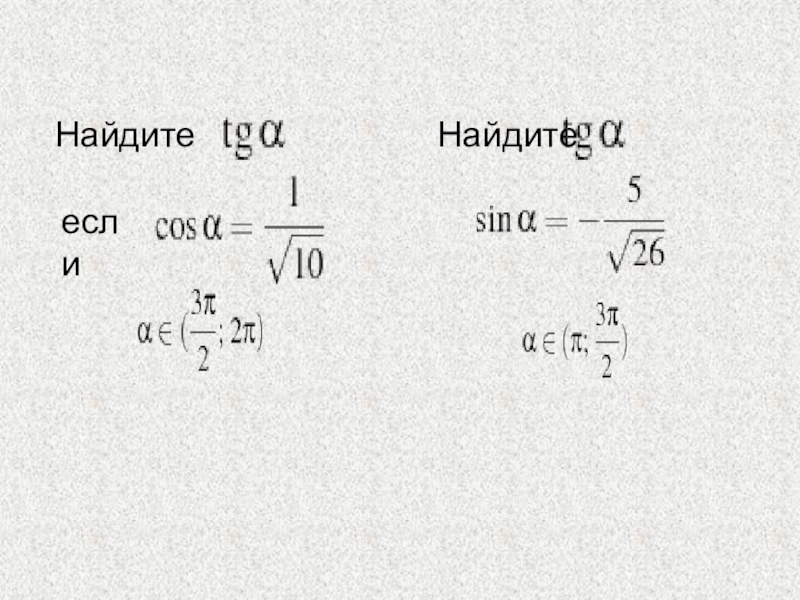- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики на тему Преобразование тригонометрических выражений
Содержание
- 1. Презентация к уроку математики на тему Преобразование тригонометрических выражений
- 2. Возникновение тригонометрииТригонометрия (trigonos-треугольник и metrio-мерю)Как и многие
- 3. Ещё древнегреческие ученые создали «тригонометрию хорд»,
- 4. Во II в. н.э. греческий ученый Птолемей
- 5. В начале XVII в. в развитии тригонометрии
- 6. Иоганн Бернулли Леонард
- 7. ТриангуляцияТриангуляция – это способ косвенного измерения больших
- 8. Триангуляцию впервые применил голландский ученый XVI в. В. Снеллиус.
- 9. ТРИАНГУЛЯЦИЯ. имеет большое научное и практическое значение.
- 10. Вершины треугольников ТРИАНГУЛЯЦИИ обозначаются на
- 11. Пункты ТРИАНГУЛЯЦИИ в целях долговременной их
- 12. Триангуляция изображения
- 13. 1)Вычислите и дайте определение функции числа
- 14. 2) Найдите значение выражения, запишите используемые формулы
- 15. Найдите Найдитеесли
- 16. Слайд 16
- 17. ВикторинаI. Какой из русских пословиц наиболее соответствует
- 18. Викторина2. Что означает слово “тригонометрия”?Тригонометрия (trigonos-треугольник и metrio-мерю)
- 19. Викторина3. Кто ввел обозначение тригонометрических функций?И. Бернулли (1642-1727) Л. Эйлер в 1748 г
- 20. Викторина4. Что такое триангуляция и кто ее
- 21. Спасибо за внимание
Возникновение тригонометрииТригонометрия (trigonos-треугольник и metrio-мерю)Как и многие разделы математики, тригонометрия возникла в древние времена из потребностей людей при ведении расчетов, связанных с земельными работами (для определения расстояния до недоступных предметов, составления географических карт и пр.).
Слайд 1
«Преобразование тригонометрических выражений»
ГПОУ ТТТ
пгт. Промышленная
Преподаватель математики
Григорьева Дарья Васильевна
Слайд 2Возникновение тригонометрии
Тригонометрия (trigonos-треугольник и metrio-мерю)
Как и многие разделы математики, тригонометрия возникла
в древние времена из потребностей людей при ведении расчетов, связанных с земельными работами (для определения расстояния до недоступных предметов, составления географических карт и пр.).
Слайд 3
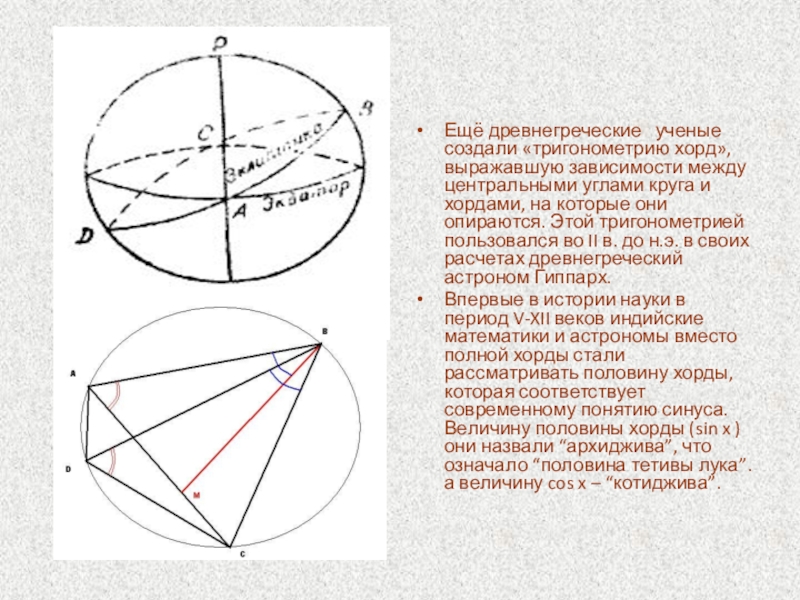
Ещё древнегреческие ученые создали «тригонометрию хорд», выражавшую зависимости между центральными
углами круга и хордами, на которые они опираются. Этой тригонометрией пользовался во II в. до н.э. в своих расчетах древнегреческий астроном Гиппарх.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды (sin x ) они назвали “архиджива”, что означало “половина тетивы лука”. а величину cos x – “котиджива”.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды (sin x ) они назвали “архиджива”, что означало “половина тетивы лука”. а величину cos x – “котиджива”.
Слайд 4Во II в. н.э. греческий ученый Птолемей в своей работе «Алмагест»
(«Великая книга») также вывел соотношения в круге, которые по своей сути аналогичны современным формулам синуса половинного и двойного углов, синуса суммы и разности двух углов.
Слайд 5В начале XVII в. в развитии тригонометрии наметилось новое направление –
аналитическое. Если до этого учения о тригонометрических функциях строились на геометрической основе, то в XVII-XIX вв. тригонометрия постепенно вошла в состав математического анализа и стала широко использоваться в механике и технике, особенно при рассмотрении колебательных процессов и иных периодических явлений.
Слайд 6Иоганн Бернулли
Леонард Эйлер
О свойствах периодичности тригонометрических функций знал ещё Ф.
Виет. Швейцарский математик
И. Бернулли (1642-1727) в своих работах начал применять символику тригонометрических функций. Однако близкую к принятой теперь, ввел
Л. Эйлер в 1748 г. в своей работе «Введение в анализ бесконечных». В ней он рассмотрел вопрос о знаках всех тригонометрических функций любого аргумента.
И. Бернулли (1642-1727) в своих работах начал применять символику тригонометрических функций. Однако близкую к принятой теперь, ввел
Л. Эйлер в 1748 г. в своей работе «Введение в анализ бесконечных». В ней он рассмотрел вопрос о знаках всех тригонометрических функций любого аргумента.
Слайд 7Триангуляция
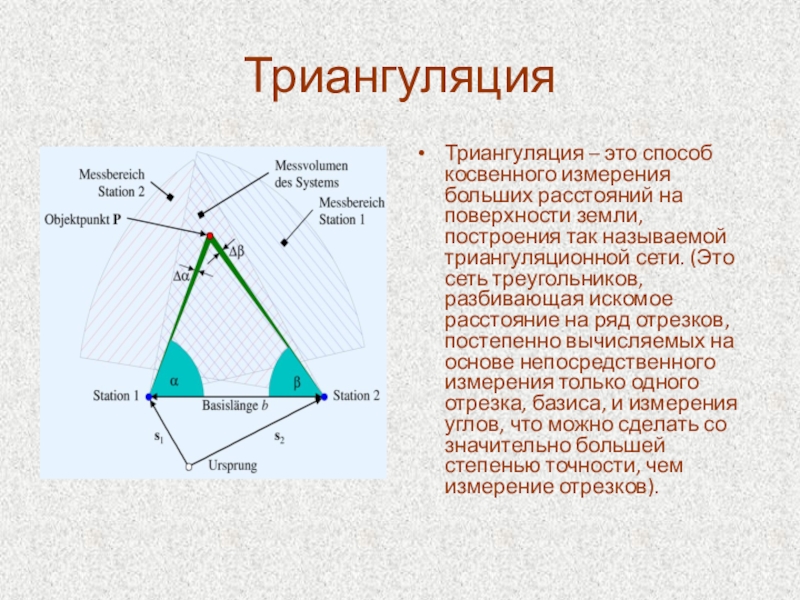
Триангуляция – это способ косвенного измерения больших расстояний на поверхности земли,
построения так называемой триангуляционной сети. (Это сеть треугольников, разбивающая искомое расстояние на ряд отрезков, постепенно вычисляемых на основе непосредственного измерения только одного отрезка, базиса, и измерения углов, что можно сделать со значительно большей степенью точности, чем измерение отрезков).
Слайд 9ТРИАНГУЛЯЦИЯ. имеет большое научное и практическое значение. Она служит для: определения
фигуры и размеров Земли методом градусных измерений; изучения горизонтальных движений земной коры; обоснования топографических съёмок в различных масштабах и целях; обоснования различных геодезических работ при изыскании, проектировании и строительстве крупных инженерных сооружений, при планировке и строительстве городов и т.д.
Слайд 10 Вершины треугольников ТРИАНГУЛЯЦИИ обозначаются на местности деревянными или металлическими
вышками высотой от 6 до 55 м в зависимости от условий местности
Слайд 11 Пункты ТРИАНГУЛЯЦИИ в целях долговременной их сохранности на местности закрепляются
закладкой в грунт особых устройств в виде металлических труб или бетонных монолитов с вделанными в них металлическими марками, фиксирующими положение точек, для которых даются координаты в соответствующих каталогах.
Слайд 131)Вычислите и дайте определение функции числа
sin 300 cos π/3 tg π/4 ctg 900
arctg 1 arcsin ½ arcctg √3 arccos √3/2
arccos(- √2/2) arctg (-1)
Слайд 16
3) Решите уравнение
а) √3cosx – sinx=1
а) √3/2 cosx – ½ sinx = 1
б) sinx + sin3x + cosx + cos3x = 0
б) sin5x + sinx = 1-2sin2x
а) √3cosx – sinx=1
а) √3/2 cosx – ½ sinx = 1
б) sinx + sin3x + cosx + cos3x = 0
б) sin5x + sinx = 1-2sin2x
Слайд 17Викторина
I. Какой из русских пословиц наиболее соответствует график функции y =
sin x и почему?
1. Чем дальше в лес, тем больше дров.
2. Дальше кумы, меньше греха.
3. Кашу маслом не испортишь.
4. Выше меры конь не скачет.
5. Пересев хуже недосева.
1. Чем дальше в лес, тем больше дров.
2. Дальше кумы, меньше греха.
3. Кашу маслом не испортишь.
4. Выше меры конь не скачет.
5. Пересев хуже недосева.
Ответ: Выше меры конь не скачет.
Пояснение: если изобразить траекторию скачущего коня, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой “мерой”.
Слайд 18Викторина
2. Что означает слово “тригонометрия”?
Тригонометрия (trigonos-треугольник и metrio-мерю)
Слайд 19Викторина
3. Кто ввел обозначение тригонометрических функций?
И. Бернулли (1642-1727)
Л. Эйлер в
1748 г
Слайд 20Викторина
4. Что такое триангуляция и кто ее придумал?
Триангуляция – это способ
косвенного измерения больших расстояний на поверхности земли.
Триангуляцию впервые применил голландский ученый XVI в. В. Снеллиус
Триангуляцию впервые применил голландский ученый XVI в. В. Снеллиус