7 посёлка Северного
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики на тему Осевая и центральная симметрия
Содержание
- 1. Презентация к уроку математики на тему Осевая и центральная симметрия
- 2. Слайд 2
- 3. “Симметрия является той идеей, посредством которой человек
- 4. Устная работа!1) 5∙(-2)+(-2)∙5=2) 24:(-8)+(-8):24=3) 12∙(-3)-(-3)∙12=4)5) 6) -20041269
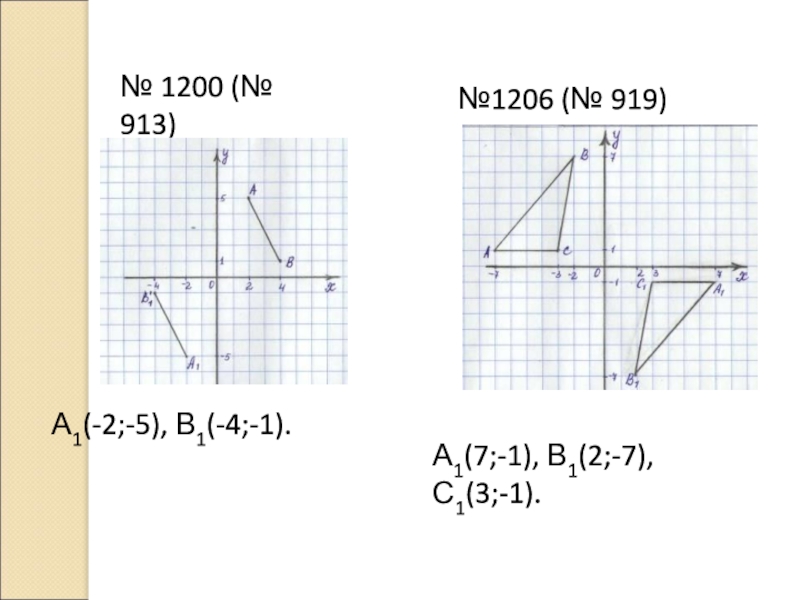
- 5. № 1200 (№ 913)А1(-2;-5), В1(-4;-1).№1206 (№ 919)А1(7;-1), В1(2;-7), С1(3;-1).
- 6. Проверочный тест
- 7. Если при сгибании плоскости чертежа по прямой,
- 8. Если при сгибании плоскости чертежа по прямой,
- 9. 11 баллов – «5»10-9 баллов - «4»8-6 баллов – «3»5-0 баллов – «2»
- 10. Симметрия Симметрия в переводе
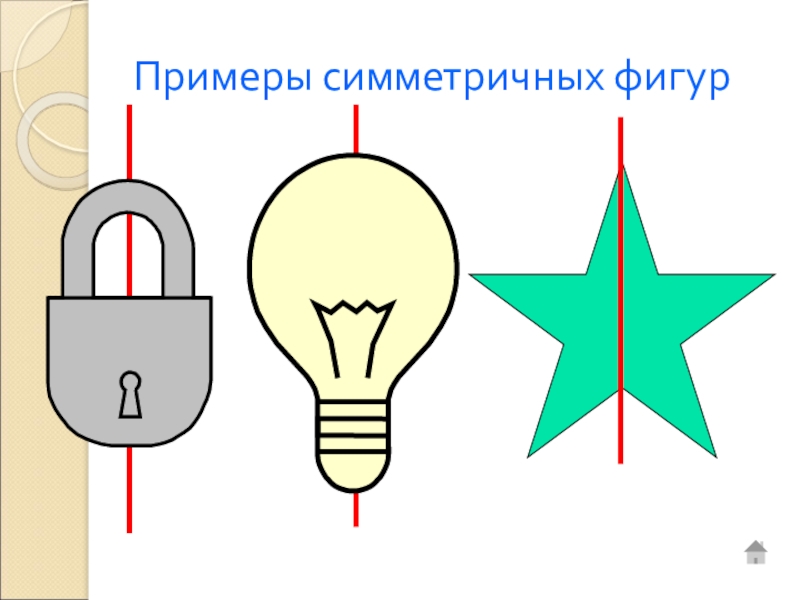
- 11. Примеры симметричных фигур
- 12. Фигуры, обладающие одной осью симметрии
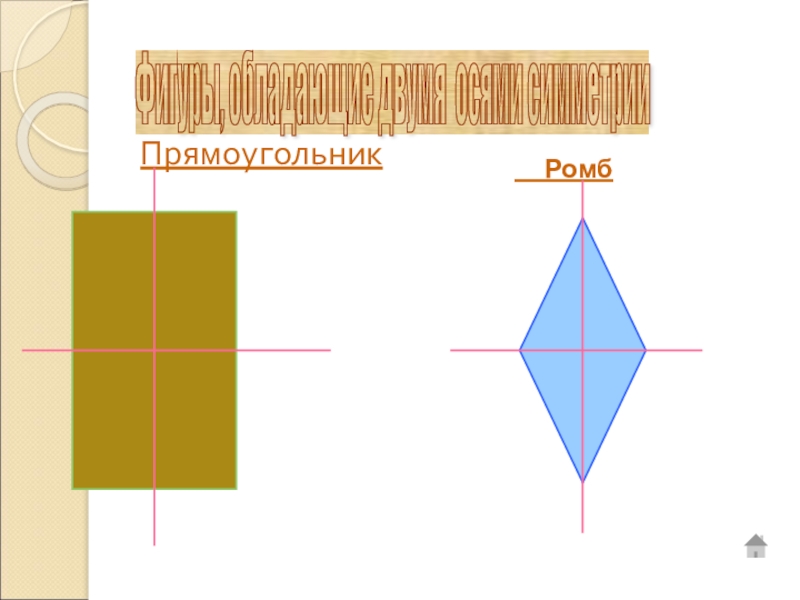
- 13. Прямоугольник РомбФигуры, обладающие двумя осями симметрии
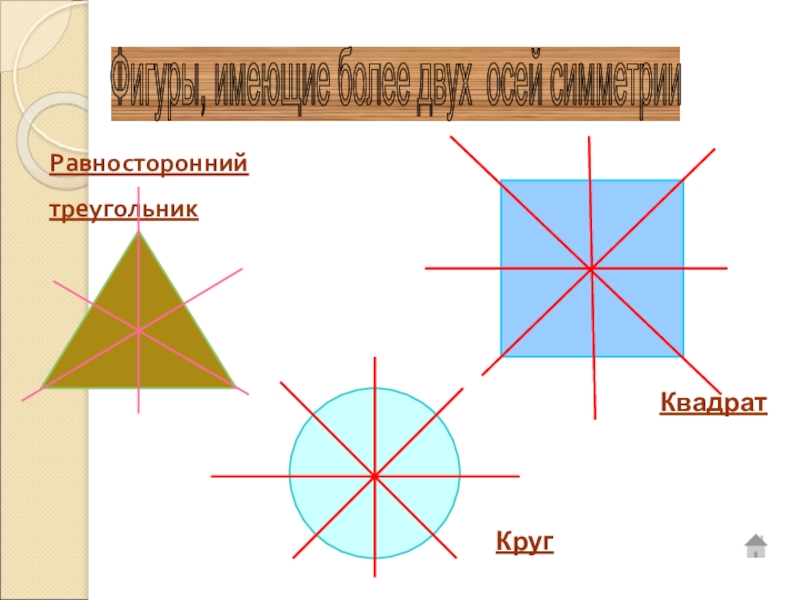
- 14. Равносторонний треугольникКвадратКругФигуры, имеющие более двух осей симметрии
- 15. Найдите лишнюю фигуруКакая из фигур, приведенных на рисунке, лишняя?Фигура 1Фигура 2Фигура 3Фигура 4Фигура 5
- 16. Эта фигура действительно лишняя, так как она
- 17. Ты не угадал! Не отчаивайся!Попробуй еще раз!
- 18. Симметрия в природе
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. В архитектуре
- 27. Байтерек.
- 28. Финляндия. Православный храм
- 29. Государственный Эрмитаж. Санкт – Петербург. Петровский зал.
- 30. Петергоф. Павильон Оранжерея.
- 31. …В гранит оделася Нева;Мосты повисли над водами;------------------------------------------------Темно-зелеными
- 32. В переводе с греческого – «бегущий обратно,
- 33. ВОР БОБРОВ !НЕСУН ГНУСЕН !
- 34. Стихотворные палиндромы называли рачьими стихами.Афанасий Фет придумал
- 35. “ИСКАТЬ ТАКСИ”, “АРГЕНТИНА МАНИТ НЕГРА”, “ЦЕНИТ НЕГРА АРГЕНТИНЕЦ”, ШОРОХ ХОРОШ.
- 36. Буквы и словаНекоторые буквы и слова имеют
- 37. ОКНО СНЕЖОК ЗВОНОК КОНЕК СЕНО СОК НОС
- 38. ХОЛОД ШАЛАШ ТОПОТ ПОТОП
- 39. Заключение Симметрию можно обнаружить почти
- 40. Слайд 40
“Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”.
Слайд 3“Симметрия является той идеей, посредством которой человек на протяжении веков пытался
постичь и создать порядок, красоту и совершенство”.
Г. Вейль
Г. Вейль
Слайд 7Если при сгибании плоскости чертежа по прямой, две фигуры совместятся, то
такие фигуры называются симметричными относительно прямой.
Если фигура некоторой прямой делится на две симметричные части, то ее называют симметричной относительно этой прямой. Прямая, относительно которой симметричны части фигуры, называются осью симметрии.
Луч, который выходит из вершины угла и делит его пополам, называется биссектрисой угла.
Прямоугольник имеет 2 оси симметрии.
Квадрат имеет 4 оси симметрии.
Окружность имеет бесконечное множество осей симметрии.
Фигура называется центрально-симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Окружность - центрально-симметричная фигура.
Отрезок - центрально-симметричная фигура.
Прямоугольник - центрально-симметричная фигура.
На координатной плоскости координаты точек, симметричных относительно точки О – начало координат, являются противоположными числами.
Если фигура некоторой прямой делится на две симметричные части, то ее называют симметричной относительно этой прямой. Прямая, относительно которой симметричны части фигуры, называются осью симметрии.
Луч, который выходит из вершины угла и делит его пополам, называется биссектрисой угла.
Прямоугольник имеет 2 оси симметрии.
Квадрат имеет 4 оси симметрии.
Окружность имеет бесконечное множество осей симметрии.
Фигура называется центрально-симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Окружность - центрально-симметричная фигура.
Отрезок - центрально-симметричная фигура.
Прямоугольник - центрально-симметричная фигура.
На координатной плоскости координаты точек, симметричных относительно точки О – начало координат, являются противоположными числами.
Слайд 8Если при сгибании плоскости чертежа по прямой, две фигуры совместятся, то
такие фигуры называются симметричными относительно прямой.
Если фигура некоторой прямой делится на две симметричные части, то ее называют симметричной относительно этой прямой. Прямая, относительно которой симметричны части фигуры, называются осью симметрии.
Луч, который выходит из вершины угла и делит его пополам, называется биссектрисой угла.
Прямоугольник имеет 2 оси симметрии.
Квадрат имеет 4 оси симметрии.
Окружность имеет бесконечное множество осей симметрии.
Фигура называется центрально-симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Окружность - центрально-симметричная фигура.
Отрезок - центрально-симметричная фигура.
Прямоугольник - центрально-симметричная фигура.
На координатной плоскости координаты точек, симметричных относительно точки О – начало координат, являются противоположными числами.
Если фигура некоторой прямой делится на две симметричные части, то ее называют симметричной относительно этой прямой. Прямая, относительно которой симметричны части фигуры, называются осью симметрии.
Луч, который выходит из вершины угла и делит его пополам, называется биссектрисой угла.
Прямоугольник имеет 2 оси симметрии.
Квадрат имеет 4 оси симметрии.
Окружность имеет бесконечное множество осей симметрии.
Фигура называется центрально-симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Окружность - центрально-симметричная фигура.
Отрезок - центрально-симметричная фигура.
Прямоугольник - центрально-симметричная фигура.
На координатной плоскости координаты точек, симметричных относительно точки О – начало координат, являются противоположными числами.
Слайд 10Симметрия
Симметрия в переводе с греческого- «summetria» соразмерность,
пропорциональность, наличие определенного порядка в расположении частей.
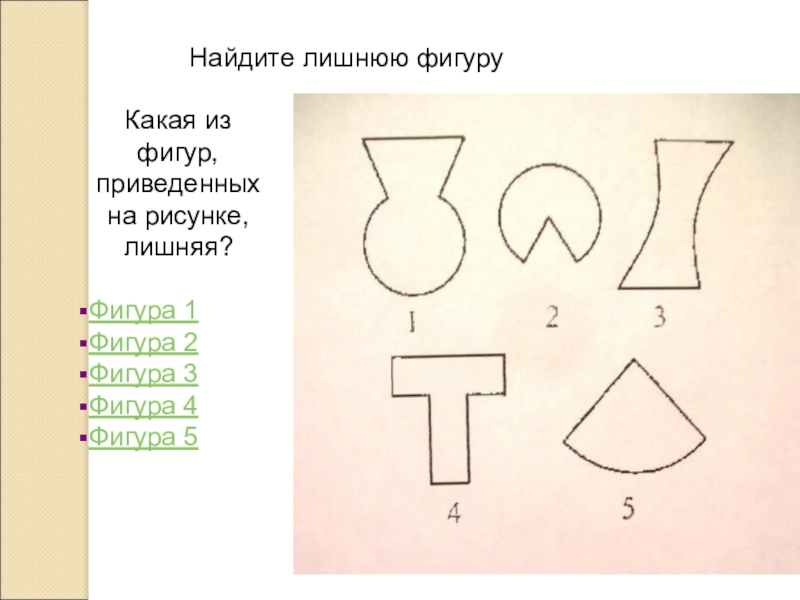
Слайд 15Найдите лишнюю фигуру
Какая из фигур, приведенных на рисунке, лишняя?
Фигура 1
Фигура 2
Фигура
3
Фигура 4
Фигура 5
Фигура 4
Фигура 5
Слайд 16Эта фигура действительно лишняя,
так как она не имеет ось симметрии
!
Перейти к слайду Перейти к слайду Симметрия в природе
Слайд 31
…В гранит оделася Нева;
Мосты повисли над водами;
------------------------------------------------
Темно-зелеными садами
Ее покрылись острова…
Пушкин А.С. «Медный всадник»
Симметрия в поэзии
Слайд 32
В переводе с греческого – «бегущий обратно, возвращающийся»
История палиндрома восходит к
глубокой древности, прежде всего античности
Впервые появились на амфорах, вазах и других предметах сферической формы.
Впервые появились на амфорах, вазах и других предметах сферической формы.
Слайд 34Стихотворные палиндромы называли рачьими стихами.
Афанасий Фет придумал выражение
А РОЗА УПАЛА НА
ЛАПУ АЗОРА
Велемир Хлебников прославился тем, что написал целую палиндром - поэму в 400 строк.
Велемир Хлебников прославился тем, что написал целую палиндром - поэму в 400 строк.
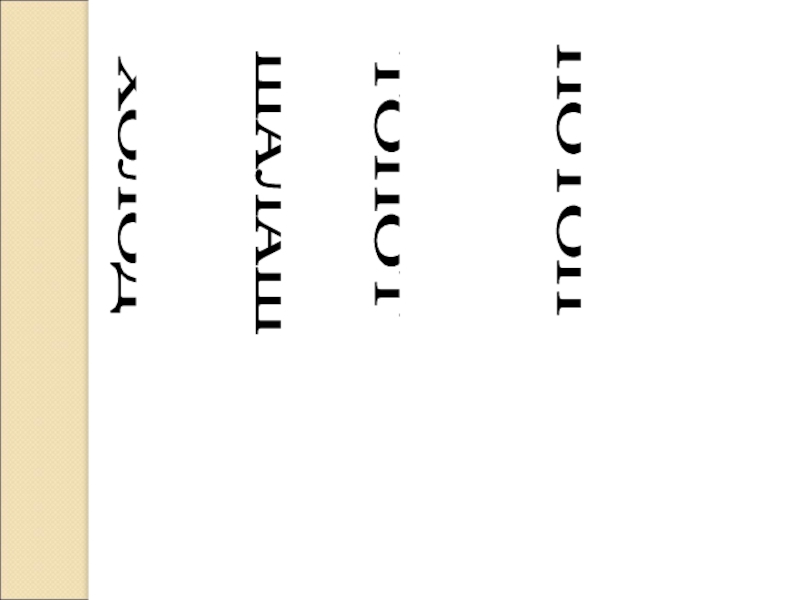
Слайд 36Буквы и слова
Некоторые буквы и слова имеют ось симметрии!
Вертикальную:
Горизонтальную:
А О П Ж Т Ф М Х Н Ш В О З С К Х Е Н Э Ю
А О П Ж Т Ф М Х Н Ш В О З С К Х Е Н Э Ю
Слайд 39Заключение
Симметрию можно обнаружить почти везде, если знать, как
ее искать. Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».