- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики на тему Обратные тригонометрические функции
Содержание
- 1. Презентация к уроку математики на тему Обратные тригонометрические функции
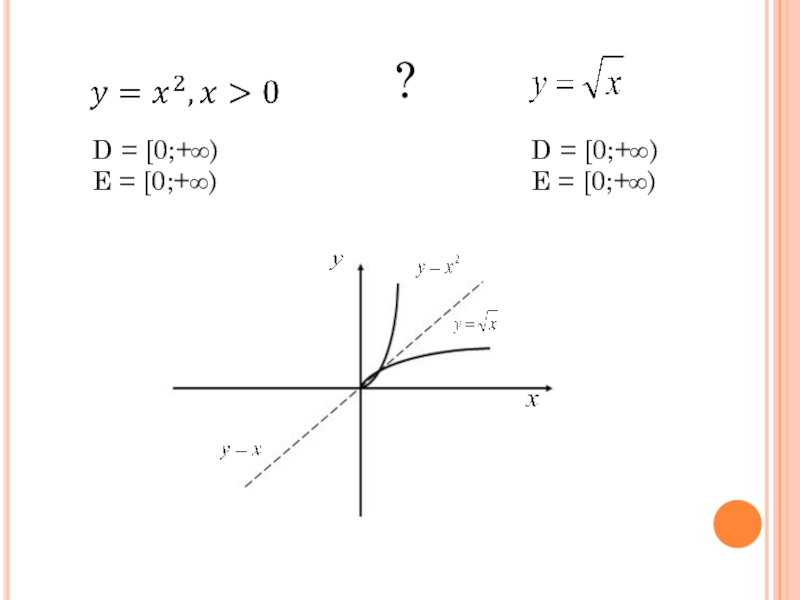
- 2. D = [0;+∞)E = [0;+∞) D = [0;+∞)E = [0;+∞) ?
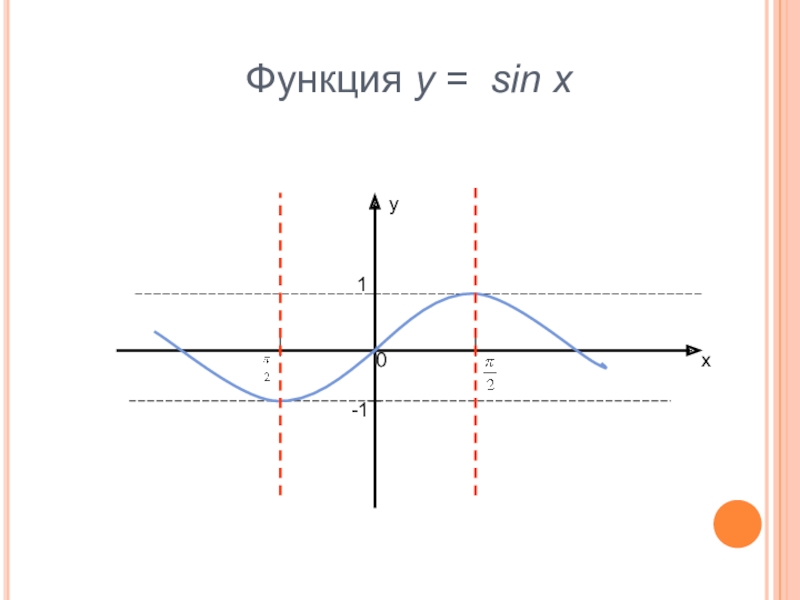
- 3. Функция у = sin xух1-10
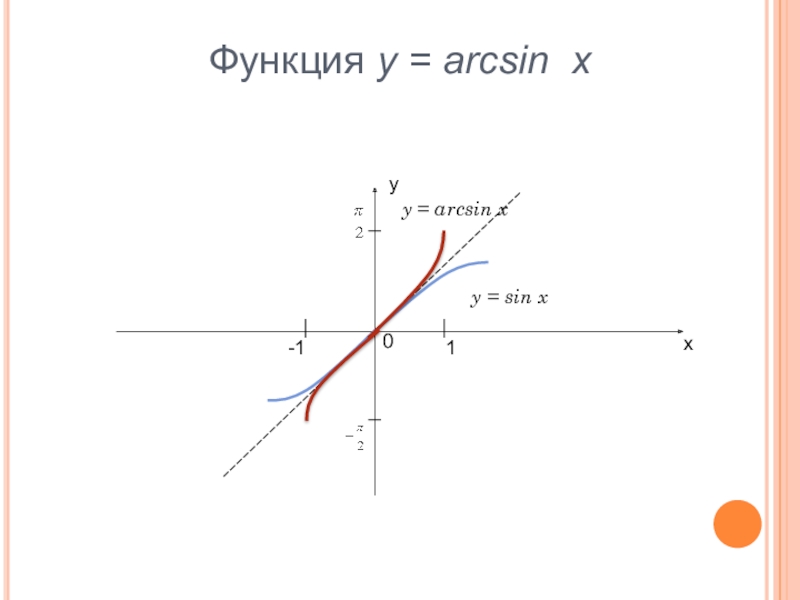
- 4. Функция y = arcsin xух0-11y = sin xy = arcsin x
- 5. Свойства функции y = arcsin xD(f) =
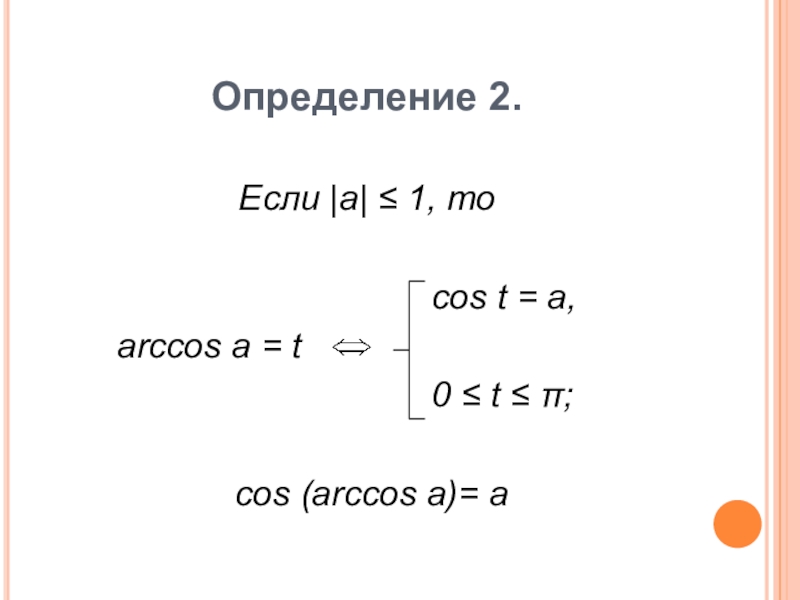
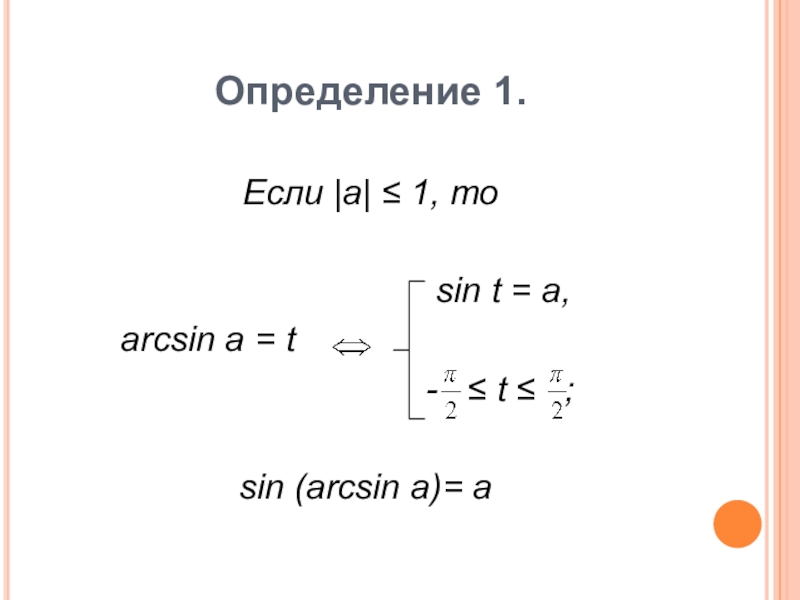
- 6. Определение 1.Если |a| ≤ 1, то
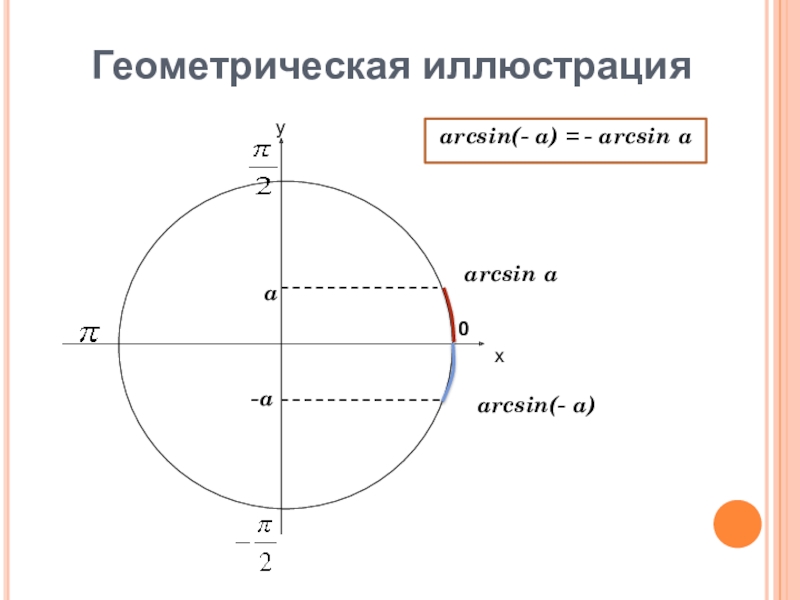
- 7. Геометрическая иллюстрацияху0arcsin aarcsin(- a)a-aarcsin(- a) = - arcsin a
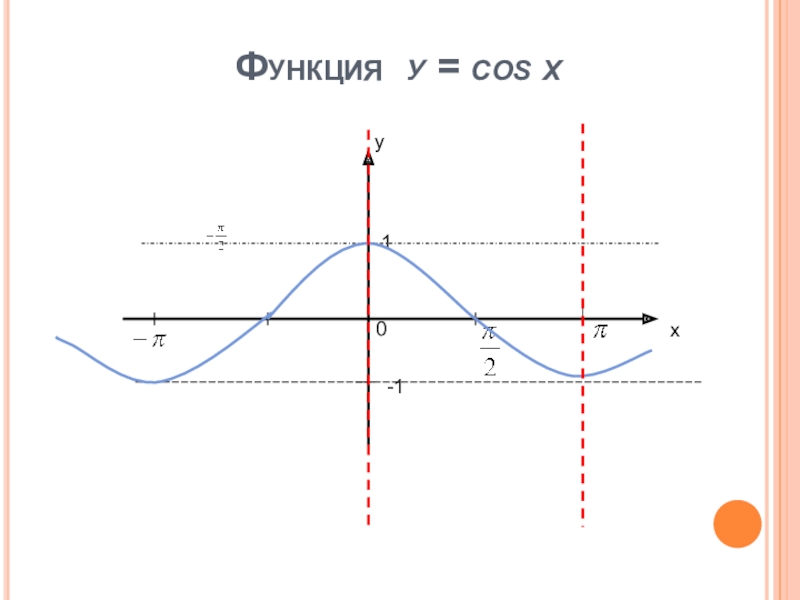
- 8. Функция у = cos xху01-1
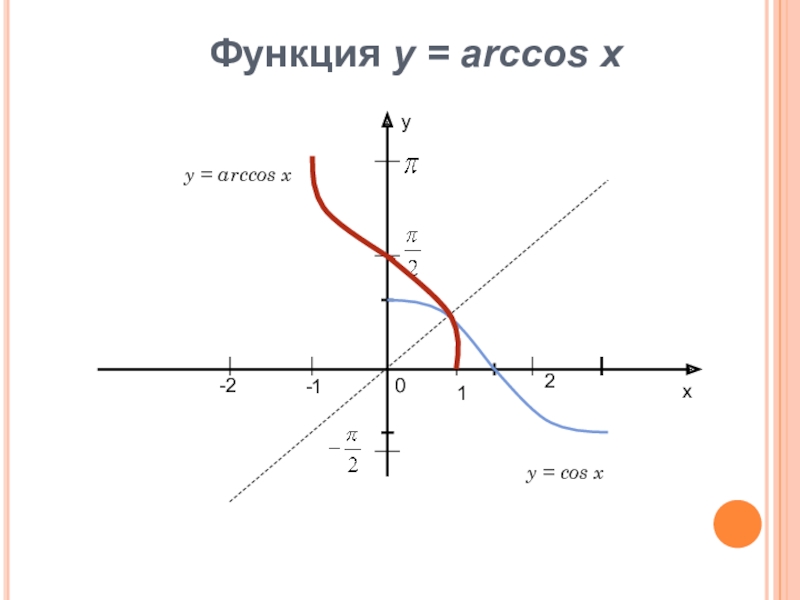
- 9. ху12-1-20Функция у = arccos xy = arccos xy = cos x
- 10. Свойства функции y = arccos xD(f) =
- 11. Определение 2.Если |a| ≤ 1, то
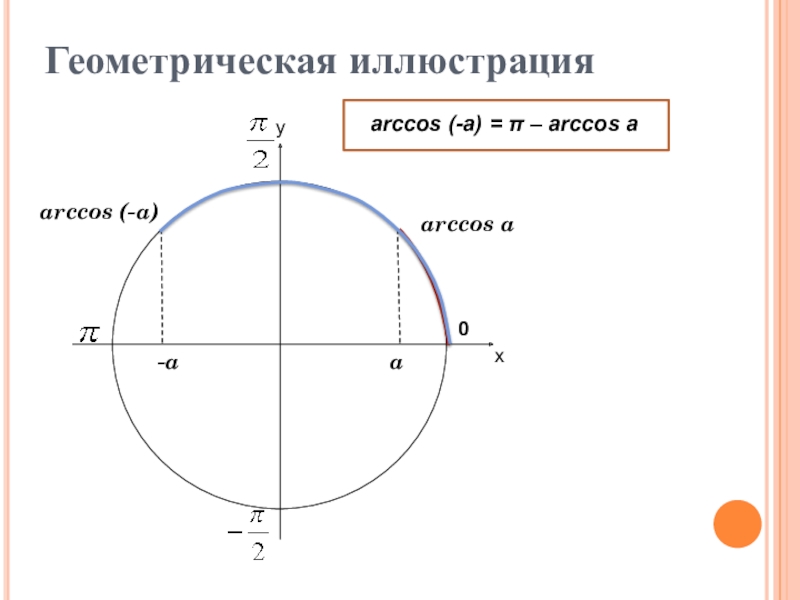
- 12. ху0Геометрическая иллюстрацияarccos aarccos (-a)-aaarccos (-a) = π – arccos a
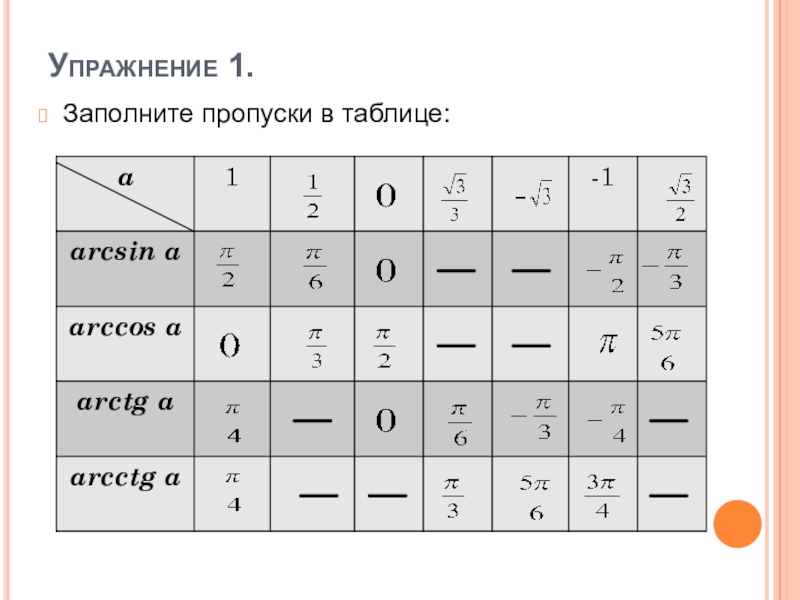
- 13. Упражнение 1.Заполните пропуски в таблице:
- 14. Упражнение 2Найдите область определения и область значений выражений:
- 15. Упражнение 3Имеет ли смысл выражение:arcsin(-1/2)
- 16. Упражнение 4Сравните числа:
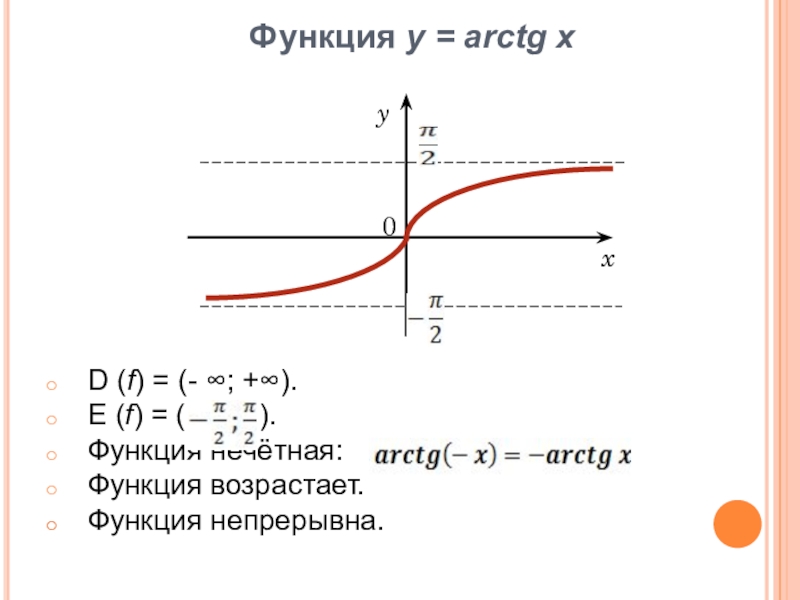
- 17. Функция у = arctg xD
- 18. Функция у = arсctg xD (f) =
- 19. Тригонометрические операции над обратными тригонометрическими функциями
- 20. Упражнение 5а) б)
- 21. Упражнение 6
- 22. Упражнение 7 Найдите наименьшее значение a,
- 23. Слайд 23
D = [0;+∞)E = [0;+∞) D = [0;+∞)E = [0;+∞) ?
Слайд 5Свойства функции y = arcsin x
D(f) = [-1;1].
E(f) = [-
; ].
Функция является нечётной:
arcsin(- x) = - arcsin x.
Функция возрастает.
Функция непрерывна.
Функция является нечётной:
arcsin(- x) = - arcsin x.
Функция возрастает.
Функция непрерывна.
Слайд 10Свойства функции y = arccos x
D(f) = [-1;1].
E(f) = [0;π ].
Функция
не является ни чётной, ни нечётной.
Функция убывает.
Функция непрерывна.
Функция убывает.
Функция непрерывна.
Слайд 15Упражнение 3
Имеет ли смысл выражение:
arcsin(-1/2)
arccos arcsin(3 - )
да нет нет
arcsin1,5 arccos(- +1 ) arccos
нет да да
да нет нет
arcsin1,5 arccos(- +1 ) arccos
нет да да
Слайд 17 Функция у = arctg x
D (f) = (- ∞;
+∞).
E (f) = ( ).
Функция нечётная:
Функция возрастает.
Функция непрерывна.
E (f) = ( ).
Функция нечётная:
Функция возрастает.
Функция непрерывна.
x
0
y
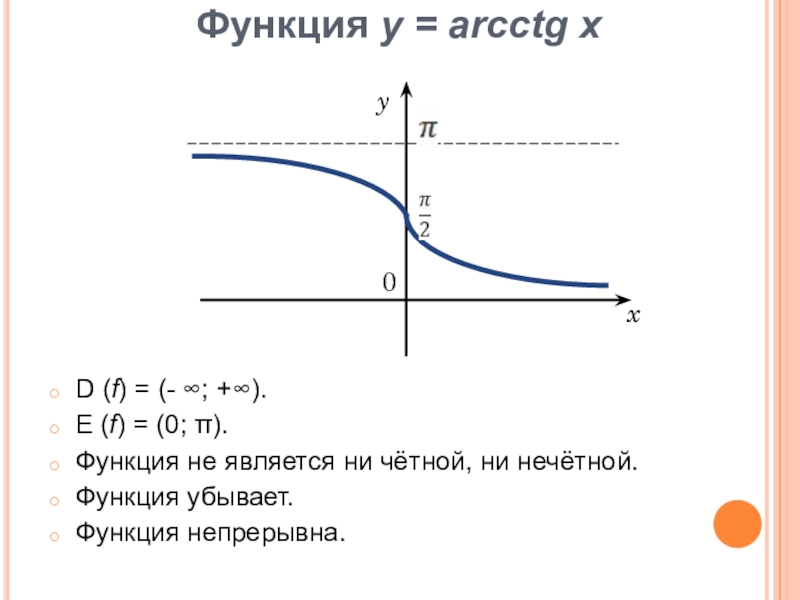
Слайд 18Функция у = arсctg x
D (f) = (- ∞; +∞).
E (f)
= (0; π).
Функция не является ни чётной, ни нечётной.
Функция убывает.
Функция непрерывна.
Функция не является ни чётной, ни нечётной.
Функция убывает.
Функция непрерывна.
y
x
0
Слайд 22Упражнение 7
Найдите наименьшее значение a, при котором существует выражение
Решение.
Значит,
наименьшее значение a = 0,25.
- 4 ≤ - 8a ≤ - 2
– 1 ≤ 3 – 8a ≤ 1
0,25 ≤ a ≤ 0,5

![Презентация к уроку математики на тему Обратные тригонометрические функции Свойства функции y = arcsin xD(f) = [-1;1].E(f) = [- ; Свойства функции y = arcsin xD(f) = [-1;1].E(f) = [- ; ].Функция является нечётной:](/img/thumbs/3bc56cf52ca36ed23aa13a707f4229ce-800x.jpg)
![Презентация к уроку математики на тему Обратные тригонометрические функции Свойства функции y = arccos xD(f) = [-1;1].E(f) = [0;π ].Функция Свойства функции y = arccos xD(f) = [-1;1].E(f) = [0;π ].Функция не является ни чётной, ни нечётной.](/img/thumbs/ff88b583c1739307d95ec3162b18f1f8-800x.jpg)