- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад исследовательского проекта по математике Особенности сферического треугольника
Содержание
- 1. Презентация исследовательского проекта по математике Особенности сферического треугольника
- 2. Любознательность — один из всегдашних верных признаков
- 3. Объект исследования: треугольник.Предмет исследования: условия, при которых треугольник может иметь три прямых угла.
- 4. Цель: Выяснить, существует ли треугольник, имеющий три прямых угла и чему равна сумма его углов.
- 5. Задачи:1. Найти дополнительную информацию о треугольниках.2. Выяснить,
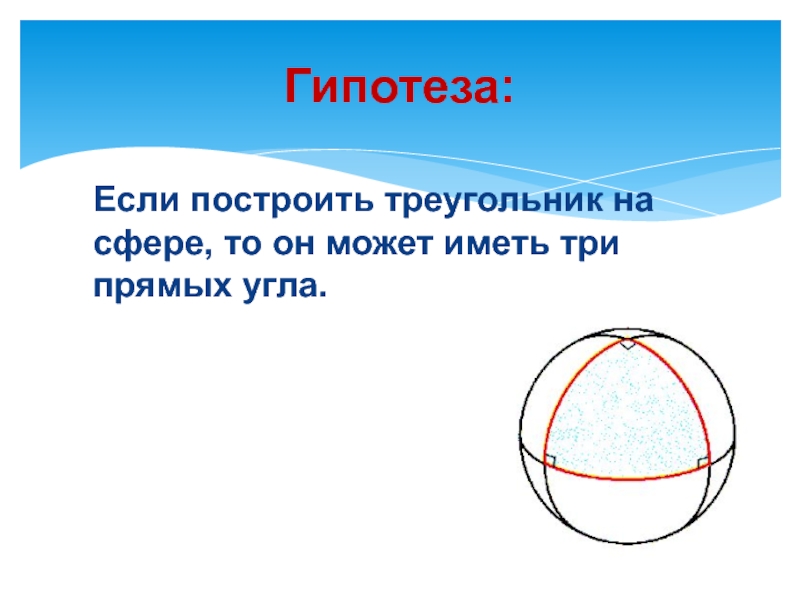
- 6. Гипотеза:Если построить треугольник на сфере, то он может иметь три прямых угла.
- 7. Методы исследования:Теоретический: изучение теоретического материала о треугольниках,
- 8. Виды геометрий.Геометрия как систематическая наука появилась в
- 9. Треугольник.Треугольником называется геометрическая фигура, состоящая из трёх
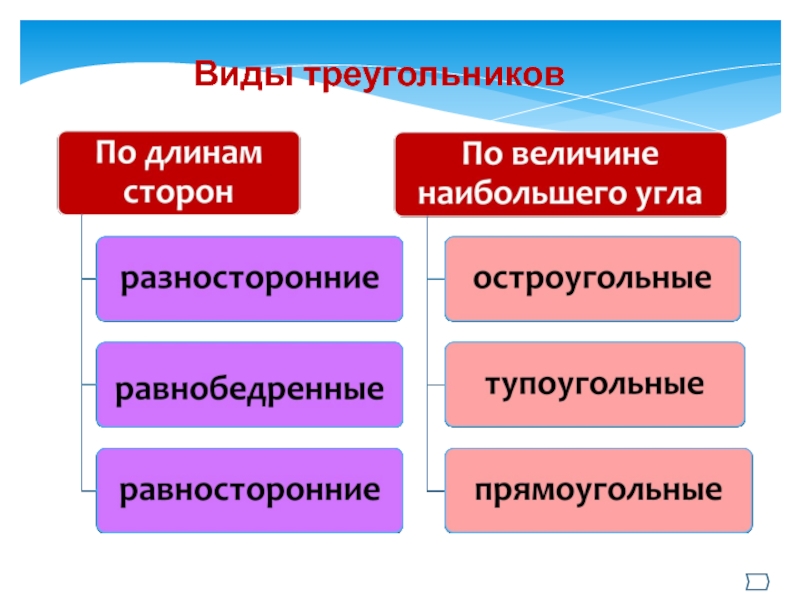
- 10. Виды треугольников
- 11. Треугольник называется остроугольным, если все его углы
- 12. Треугольник, у которого три стороны имеют различную
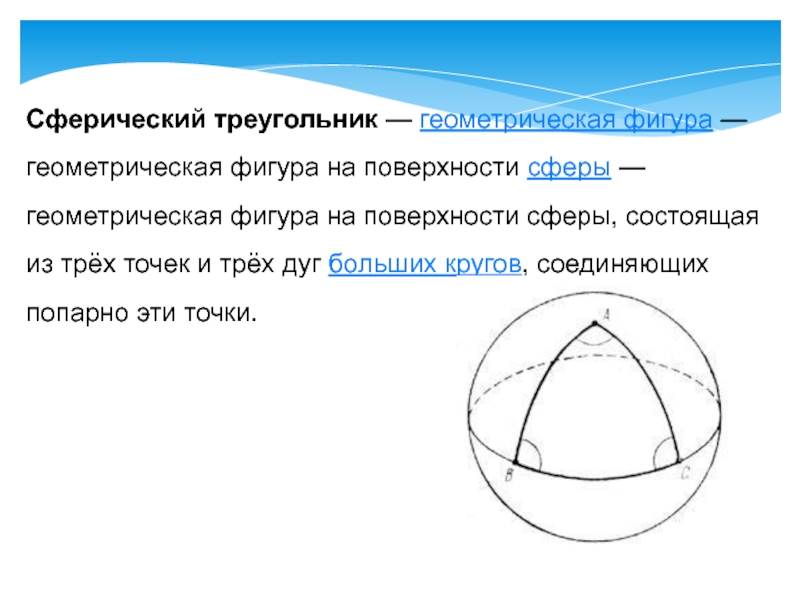
- 13. Сферический треугольник — геометрическая фигура — геометрическая фигура на
- 14. Сумма углов треугольника.Теорема о сумме углов треугольника —
- 15. Практическая работа «Сумма углов треугольника».В ходе
- 16. Этапы выполнения работы:1). Организационный: подготовка необходимого материала
- 17. Изготовление модели треугольника, имеющего 3 прямых угла.Таким
- 18. Заключение. Работа с дополнительной литературой позволила не
- 19. Информационные ресурсы. Ананасян Л.С., БутузовВ.Ф., Кадомцев С.Б.,
Слайд 1
ОСОБЕННОСТИ СФЕРИЧЕСКОГО ТРЕУГОЛЬНИКА
Выполнил: Алий Николай
ученик 5Б класса
Руководитель: Говердовская Ирина Николаевна
учитель математики
Слайд 2Любознательность — один из всегдашних верных признаков энергичного ума.
Джонсон Сэмюэль
При изучении
Меня очень заинтересовала эта тема и я решил найти дополнительную информацию в книгах, Интернете и других источниках. Изучить этот вопрос более подробно.
Слайд 3Объект исследования: треугольник.
Предмет исследования: условия, при которых треугольник может иметь три
Слайд 4Цель:
Выяснить, существует ли треугольник, имеющий три прямых угла и чему
Слайд 5Задачи:
1. Найти дополнительную информацию о треугольниках.
2. Выяснить, может ли сумма углов
3. Изготовить модель треугольника, имеющего три прямых угла.
Слайд 7Методы исследования:
Теоретический: изучение теоретического материала о треугольниках, их видах и сумме
Моделирование: изготовление модели треугольника, имеющего три прямых угла.
Слайд 8Виды геометрий.
Геометрия как систематическая наука появилась в Древней ГрецииГеометрия как систематическая
Наряду с евклидовой геометрией (геометрия на плоскости, пространстве), существует и неевклидовая геометрия. Одной из ее разновидностей является сферическая геометрия. И треугольники, рассматриваемые в такой геометрии, являются сферическими и обладают свойствами, отличными от общепринятых и общеизвестных.
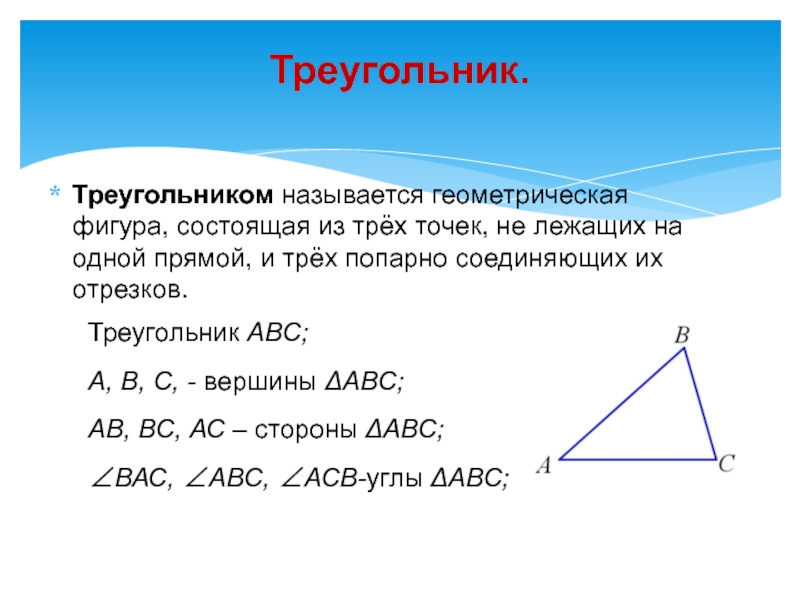
Слайд 9Треугольник.
Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на
Треугольник АВС;
А, В, С, - вершины ΔАВС;
АВ, ВС, АС – стороны ΔАВС;
∠ВАС, ∠АВС, ∠АСВ-углы ΔАВС;
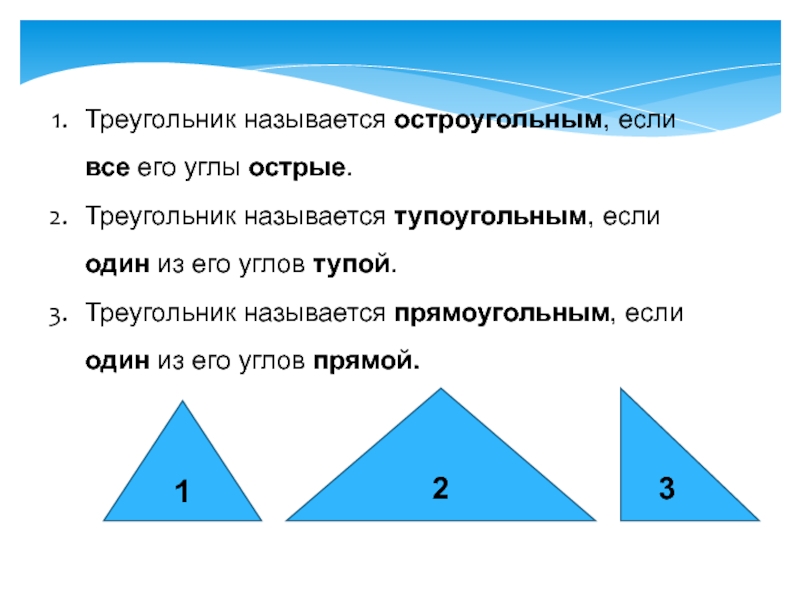
Слайд 11Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным,
Треугольник называется прямоугольным, если один из его углов прямой.
1
2
3
Слайд 12
Треугольник, у которого три стороны имеют
различную длину, называют
разносторонним треугольником.
Если
его называют равнобедренным треугольником.
△ ABC – равнобедренный
Если три стороны треугольника равны, то его
называют равносторонним треугольником.[3]
Слайд 13
Сферический треугольник — геометрическая фигура — геометрическая фигура на поверхности сферы — геометрическая фигура
Слайд 14Сумма углов треугольника.
Теорема о сумме углов треугольника
— классическая теорема евклидовой
геометрии. Утверждает,
треугольника равна 180˚.
Угол между меридианами на северном полюсе - 90˚.
Две другие вершины лежат на экваторе,
соответствующие углы равны 90°. Значит,
у сферического треугольника могут быть
два или даже три прямых или тупых угла.
Таким образом, сумма углом такого
сферического треугольника равна 270˚.
Слайд 15Практическая работа
«Сумма углов треугольника».
В ходе работы с помощью транспортира измеряли
Слайд 16Этапы выполнения работы:
1). Организационный: подготовка необходимого материала для изготовления модели сферического
2) Основной: изготовление модели сферы.
3) Заключительный: изготовление сферического треугольника с тремя прямыми углами.
Для этого надо найти точку на экваторе провести линию до северного полюса и провести линию к экватору при этом, сохраняя углы по девяносто градусов.
Изготовление модели треугольника, имеющего 3 прямых угла.
Слайд 17Изготовление модели треугольника, имеющего 3 прямых угла.
Таким образом, я изготовил модель
сферического
прямыми углами.
Данный треугольник является еще
и равносторонним.
Слайд 18Заключение.
Работа с дополнительной литературой позволила не только найти необходимый материал по
Работая на проектом, я изучили разделы математики, изучаемые в 7 классе. Нашел теоретический материал и доказал, что сумма углов треугольника не всегда равна 180˚. Узнал условия, способствующие наличию у треугольника трех прямых углов.
Научился изготавливать модель сферического треугольника.
Слайд 19Информационные ресурсы.
Ананасян Л.С., БутузовВ.Ф., Кадомцев С.Б., Поздняк Э.Г., Юдина И.И.Геометрия 7-9
Вигасин А. А., Годер Г. И., Свенцицкая И. С. История древнего мира; учеб. Для 5 кл. общеобразоват. Учреждений. М.: Просвещение 2001
Математика. Еженедельная учебно-методическая газета, № 12. 2003
Мерзляк А.Г., Полонский В.Б., Якир М.С., Издательский центр «Вента-Граф». 2012
https://ru.wikipedia.org/wiki/Геометрия
tmath.ru/1/2/1/1/page.php
https://bigenc.ru/mathematics/text/2652171