2017
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для учителей математики
Содержание
- 1. Презентация для учителей математики
- 2. Современная действительность требует от школы выпускников, умеющих
- 3. Одной из основных задач школьного математического образования
- 4. Существенную роль в развитии способностей учащихся к
- 5. «Натуральные числа. Свойства сложения и умножения» 5
- 6. «Простые и составные числа» 6 класс.Задача.Как известно,
- 7. Слайд 7
- 8. «Площадь прямоугольника. Площадь квадрата»
- 9. Слайд 9
- 10. «Окружность и круг» 6 классЗадача.1) Постройте окружность
- 11. «Умножение дробей» 6 классЗадача.Отвечая на вопросы 1
Современная действительность требует от школы выпускников, умеющих творчески мыслить и принимать нестандартные решения. Основная задача школы состоит не только в том, чтобы дать учащимся глубокие знания, но в том чтобы научить их самостоятельно решать возникающие проблемы.
Слайд 1Роль исследовательских заданий при изучении математики
учитель математики
МОУ Романовская СОШ
Непряхина
Е.В.
Слайд 2Современная действительность требует от школы выпускников, умеющих творчески мыслить и принимать
нестандартные решения.
Основная задача школы состоит не только в том, чтобы дать учащимся глубокие знания, но в том чтобы научить их самостоятельно решать возникающие проблемы.
Основная задача школы состоит не только в том, чтобы дать учащимся глубокие знания, но в том чтобы научить их самостоятельно решать возникающие проблемы.
Слайд 3Одной из основных задач школьного математического образования является развитие самостоятельности и
творческой активности учащихся, овладение ими исследовательскими навыками.
Решение этой задачи возможно, если учебный материал дается учащимся не в готовом виде, а как объект поиска.
Основная нагрузка в процессе обучения должна падать не на память учащихся, а на их мышление.
Решение этой задачи возможно, если учебный материал дается учащимся не в готовом виде, а как объект поиска.
Основная нагрузка в процессе обучения должна падать не на память учащихся, а на их мышление.
Слайд 4Существенную роль в развитии способностей учащихся к самостоятельным исследованиям играют задания,
выполнение которых представляет собой относительно завершенный исследовательский цикл: наблюдение – гипотеза – проверка гипотезы.
Задачи – исследования – это эффективное средство повышения активности школьников.
Задачи – исследования – это эффективное средство повышения активности школьников.
Слайд 5«Натуральные числа. Свойства сложения и умножения»
5 класс.
Задача.
Проверьте равенство: 1+3=22, 1+3+5=32,
1+3+5+7=42
Эти равенства подсказывают прием вычисления суммы последовательных нечетных чисел. В чём состоит этот приём? Запишите следующее равенство и проверьте себя с помощью вычислений.
2) Пользуясь рассмотренным приемом, найдите:
а) сумму первых десяти нечетных чисел;
б) сумму всех нечетных чисел от 1 до 99
Слайд 6«Простые и составные числа» 6 класс.
Задача.
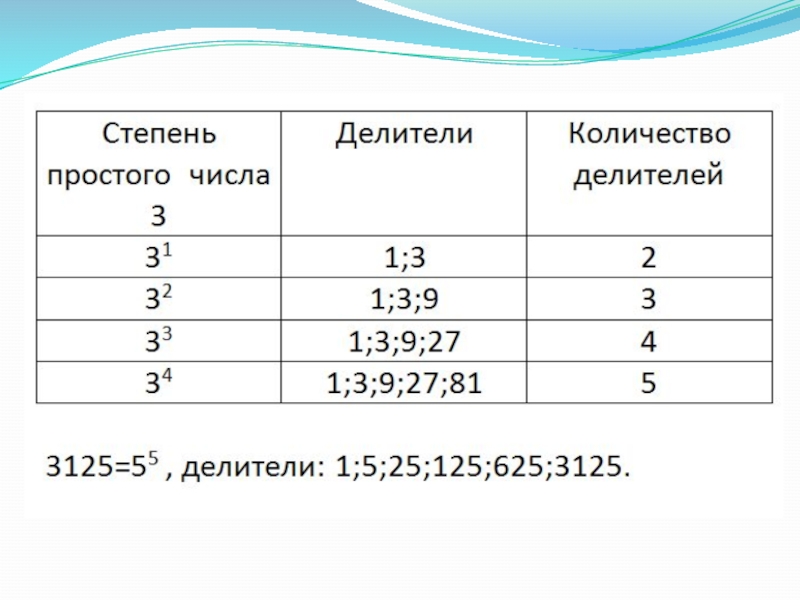
Как известно, простое число имеет два
делителя. А сколько делителей имеет квадрат простого числа? куб простого числа? четвертая степень простого числа? Выясните это на конкретных примерах.
Как вы думаете, сколько делителей имеет пятая степень простого числа?
3) Перечислите все делители числа 3125 (подсказка 3125=55 )
Как вы думаете, сколько делителей имеет пятая степень простого числа?
3) Перечислите все делители числа 3125 (подсказка 3125=55 )
Слайд 8«Площадь прямоугольника. Площадь квадрата» 5 класс
Задача.
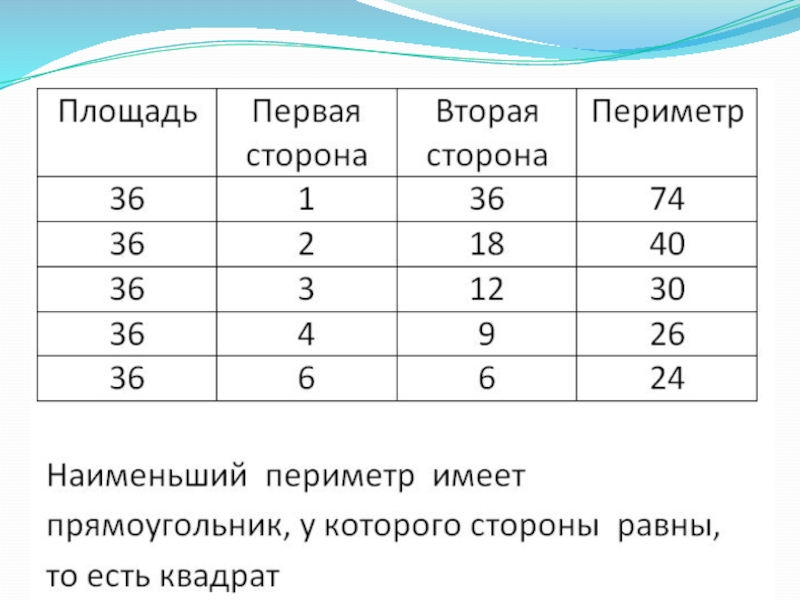
Площадь прямоугольника равна
36 см2 . Какими могут быть длины его сторон? Рассмотрите все возможные варианты. Какими могут быть периметры соответствующих прямоугольников
2) Какой из прямоугольников имеет наименьший периметр?
2) Какой из прямоугольников имеет наименьший периметр?
Слайд 10«Окружность и круг» 6 класс
Задача.
1) Постройте окружность и проведите её диаметр
AB. Постройте угол АСВ с вершиной С, лежащей на окружности. Каким (острым, прямым или тупым) является этот угол? Постройте и измерьте ещё два угла с вершинами на окружности, «опирающиеся» на диаметр. Какой вывод можно сделать.
Слайд 11«Умножение дробей» 6 класс
Задача.
Отвечая на вопросы 1 и 2, поэкспериментируйте с
числами
1 ) Известно, что m>1. Сравните числа: m и m2 ; m2 и m3
2 ) Известно, что m<1. Сравните числа: m и m2 ; m2 и m3
3) Как меняется число при возведении его в степень, если оно больше 1? Меньше 1?
4 ) Сравните m20 и m30 если:
а ) m > 1
б) m < 1
1 ) Известно, что m>1. Сравните числа: m и m2 ; m2 и m3
2 ) Известно, что m<1. Сравните числа: m и m2 ; m2 и m3
3) Как меняется число при возведении его в степень, если оно больше 1? Меньше 1?
4 ) Сравните m20 и m30 если:
а ) m > 1
б) m < 1