- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентации к урокам математики
Содержание
Теорема. В любой треугольник можно вписать окружность.Доказательство:Рассмотрим ΔАВС.Проведем биссектрисы треугольника, пересекающиеся в точке О.Проведем перпендикуляры ОК, ОL и ОM к сторонам ΔАВС.
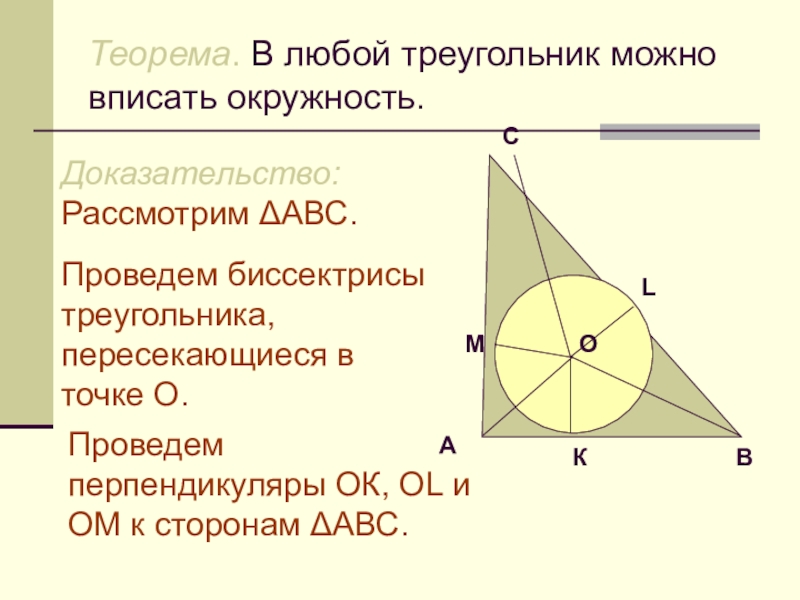
Слайд 2Теорема. В любой треугольник можно вписать окружность.
Доказательство:
Рассмотрим ΔАВС.
Проведем биссектрисы треугольника, пересекающиеся
в точке О.
Проведем перпендикуляры ОК, ОL и ОM к сторонам ΔАВС.
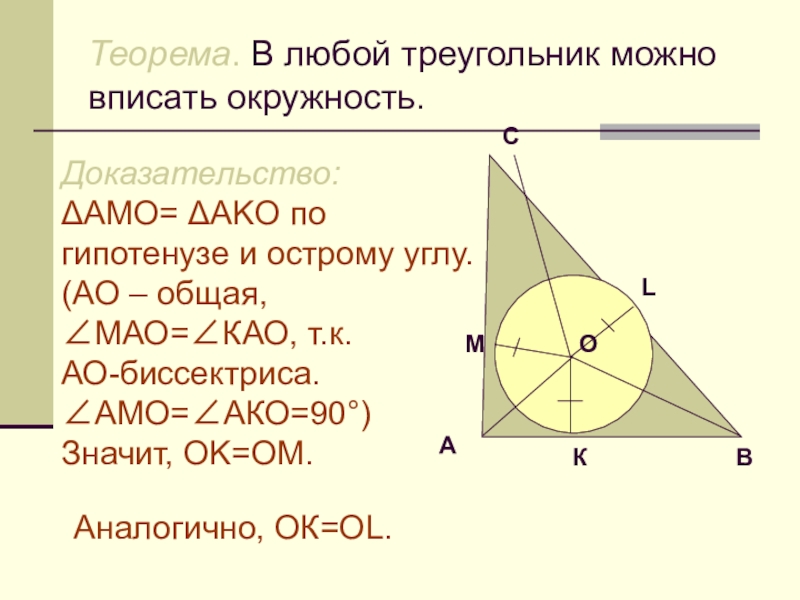
Слайд 3Теорема. В любой треугольник можно вписать окружность.
Доказательство:
ΔАMO= ΔАKO по гипотенузе и
острому углу.
(AO – общая,
∠МАО=∠КАО, т.к.
АО-биссектриса.
∠АМО=∠АКО=90°)
Значит, OK=OM.
(AO – общая,
∠МАО=∠КАО, т.к.
АО-биссектриса.
∠АМО=∠АКО=90°)
Значит, OK=OM.
Аналогично, ОК=OL.
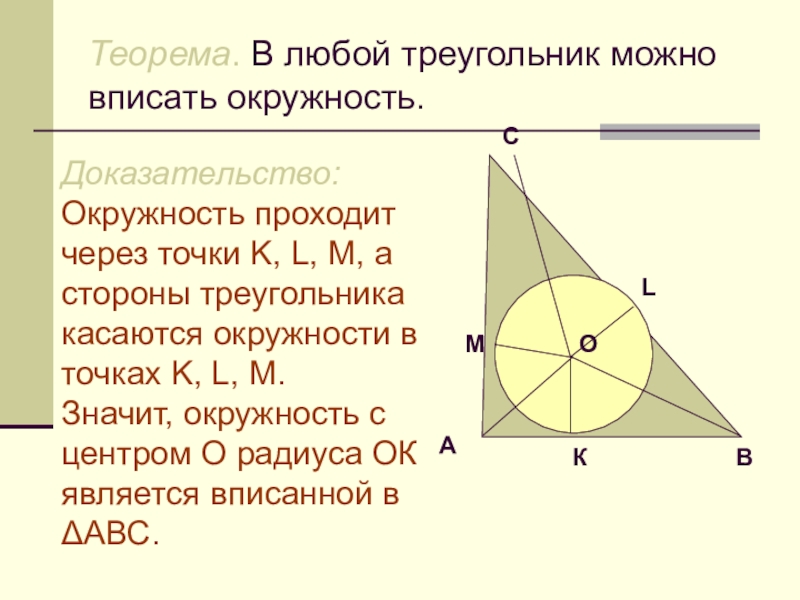
Слайд 4Теорема. В любой треугольник можно вписать окружность.
Доказательство:
Окружность проходит через точки K,
L, M, а стороны треугольника касаются окружности в точках K, L, M.
Значит, окружность с центром О радиуса ОК является вписанной в ΔАВС.
Значит, окружность с центром О радиуса ОК является вписанной в ΔАВС.