- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Обоснование евклидовой геометрии
Содержание
- 1. Обоснование евклидовой геометрии
- 2. Основными объектами в аксиоматике Смирновых являются точки,
- 3. Первая группа аксиом относится к взаимному расположению
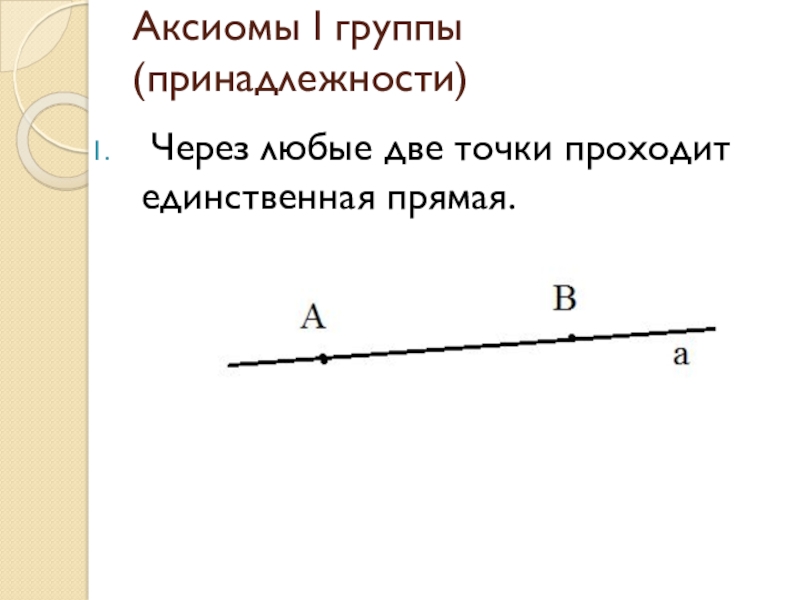
- 4. Аксиомы I группы (принадлежности) Через любые две точки проходит единственная прямая.
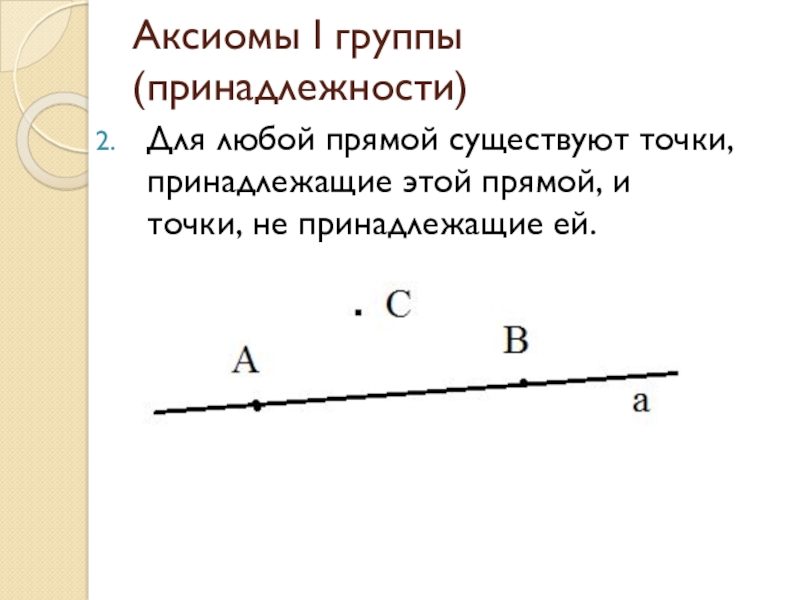
- 5. Аксиомы I группы (принадлежности)Для любой прямой существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
- 6. Аксиомы I группы (взаимного расположения точек на
- 7. Аксиомы I группы (взаимного расположения точек на
- 8. Опр. Часть прямой, состоящая из двух данных
- 9. Аксиомы I группы Каждая прямая на плоскости
- 10. Опр. Часть прямой, состоящая из данной точки
- 11. Одной из основных операций, которую можно производить
- 12. Опр. Если на отрезке АВ между точками
- 13. Чтобы сложить два произвольных отрезка AB и
- 14. Используя операцию сложения отрезка с самим собой,
- 15. Аксиомы II группы (относятся к понятию равенства
- 16. Аксиомы II группыДва отрезка, равные третьему, равны
- 17. Опр. Фигура, образованная двумя лучами с общей
- 18. Одной из основных операций, которую можно производить
- 19. Если внутри угла АОВ провести
- 20. Аксиомы III группы (равенство углов)Каждый угол равен
- 21. Опр. Фигура, образованная простой замкнутой ломаной и
- 22. Два треугольника называются равными, если стороны одного
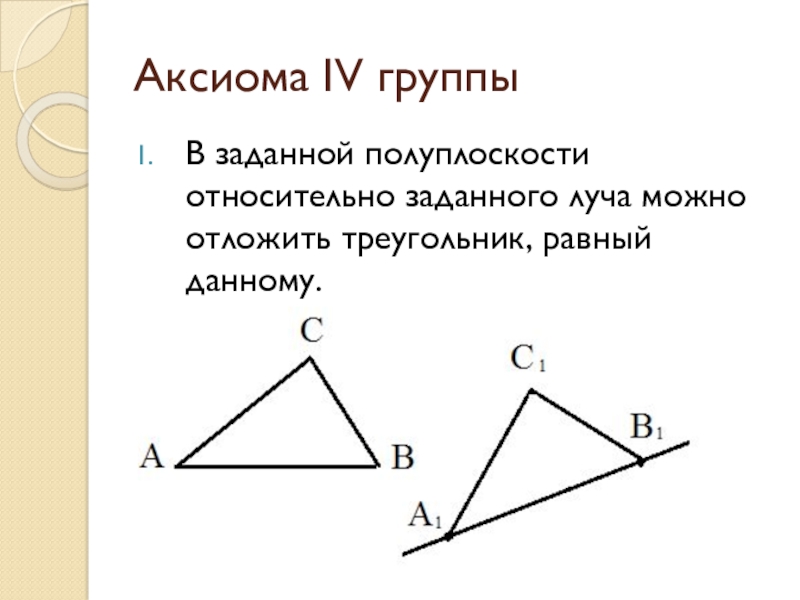
- 23. Аксиома IV группыВ заданной полуплоскости относительно заданного луча можно отложить треугольник, равный данному.
- 24. Опр. Окружностью называется геометрическая фигура, состоящая из
- 25. Аксиома V группы:Если расстояние между центрами двух
- 26. Опр. Две прямые на плоскости называются параллельными, если они не пересекаются, т.е. не имеют общих точек.
- 27. Аксиома VI группы (аксиома параллельных)Через точку, не
- 28. Опр. Координатной прямой называется прямая, на которой
- 29. Опр. Координатой точки А на координатной прямой
- 30. Аксиома VII группы (аксиома непрерывности) Соответствие, при
- 31. Это означает, что каждой точке координатной прямой
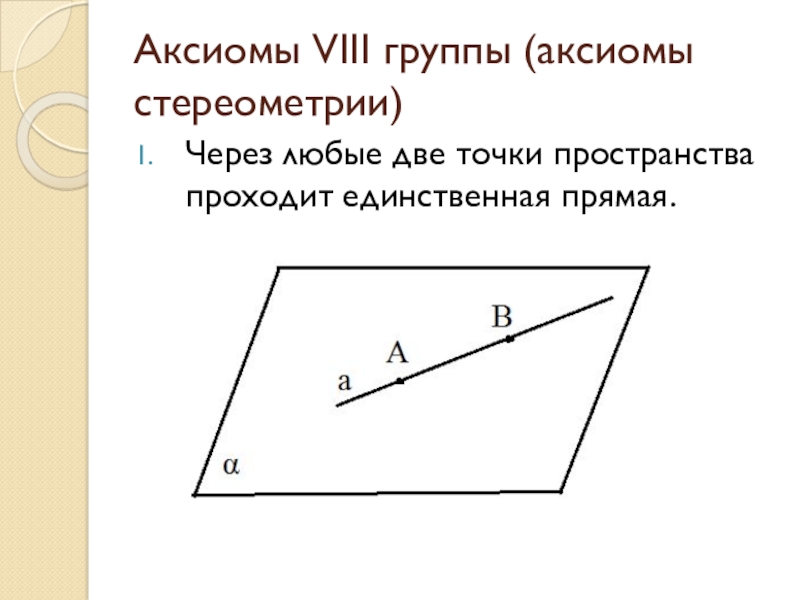
- 32. Аксиомы VIII группы (аксиомы стереометрии)Через любые две точки пространства проходит единственная прямая.
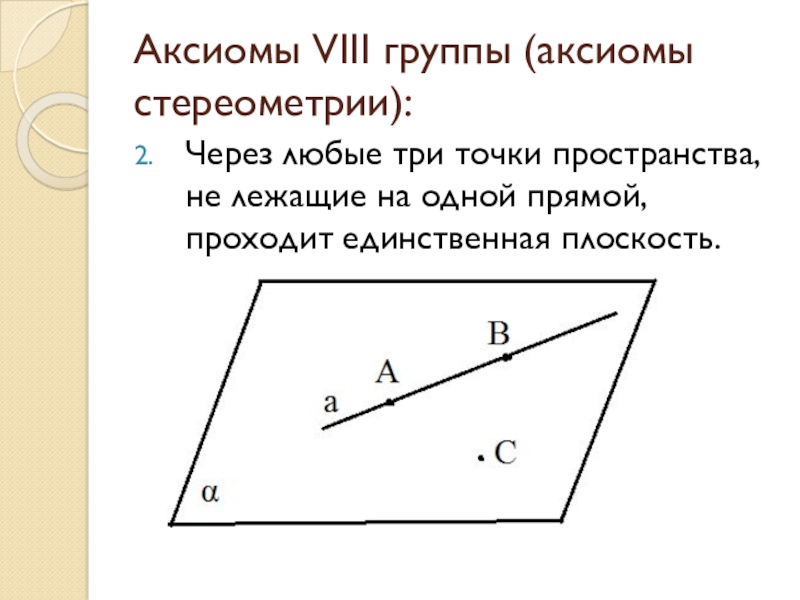
- 33. Аксиомы VIII группы (аксиомы стереометрии):Через любые три
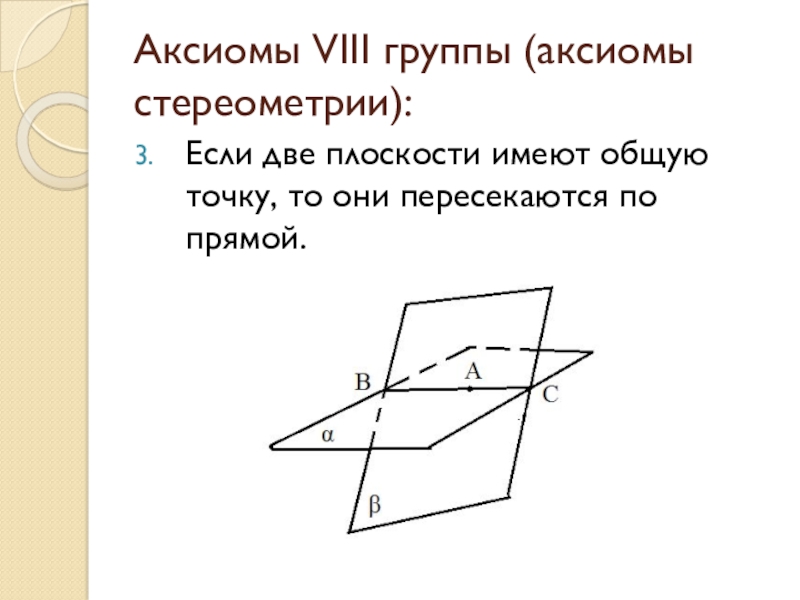
- 34. Аксиомы VIII группы (аксиомы стереометрии):Если две плоскости имеют общую точку, то они пересекаются по прямой.
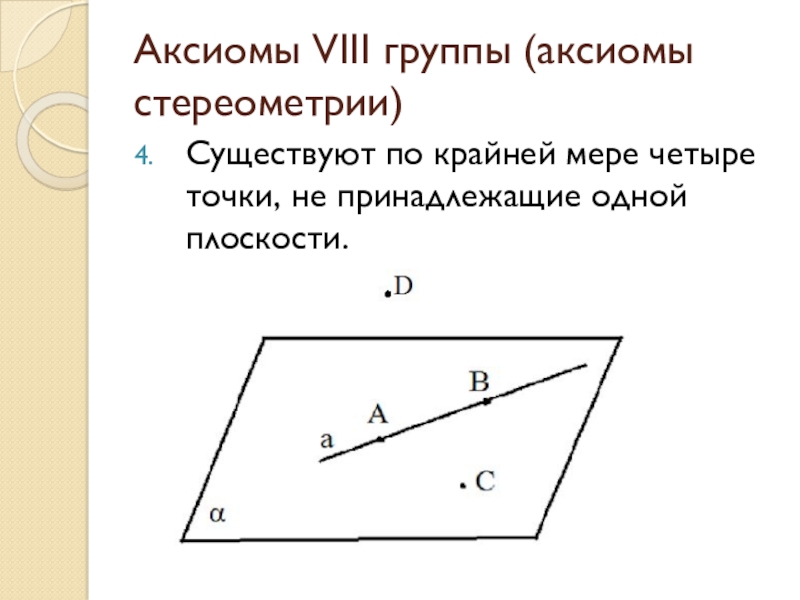
- 35. Аксиомы VIII группы (аксиомы стереометрии)Существуют по крайней мере четыре точки, не принадлежащие одной плоскости.
- 36. Опр. Два угла называются вертикальными, если стороны
- 37. Дано: AOC и
Основными объектами в аксиоматике Смирновых являются точки, прямые и плоскости. За основные отношения примем: «принадлежность», «лежать между». Точка, прямая и плоскость являются основными геометрическими фигурами в том смысле, что остальные фигуры определяются через них. Сами же
Слайд 2Основными объектами в аксиоматике Смирновых являются точки, прямые и плоскости. За
основные отношения примем: «принадлежность», «лежать между».
Точка, прямая и плоскость являются основными геометрическими фигурами в том смысле, что остальные фигуры определяются через них. Сами же основные фигуры не определяются, а указываются свойства, которым они удовлетворяют. Эти свойства называются аксиомами.
Точка, прямая и плоскость являются основными геометрическими фигурами в том смысле, что остальные фигуры определяются через них. Сами же основные фигуры не определяются, а указываются свойства, которым они удовлетворяют. Эти свойства называются аксиомами.
Слайд 3 Первая группа аксиом относится к взаимному расположению точек и прямых на
плоскости. Точки обозначаются: A, B, C, D, … . Прямые обозначаются: a, b, c, … или AB, BC, … .
Слайд 5Аксиомы I группы (принадлежности)
Для любой прямой существуют точки, принадлежащие этой прямой,
и точки, не принадлежащие ей.
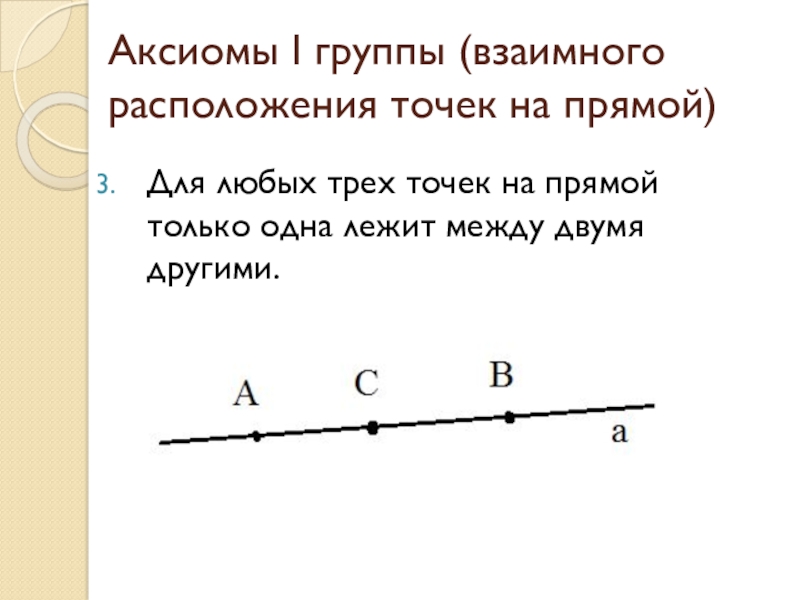
Слайд 6Аксиомы I группы (взаимного расположения точек на прямой)
Для любых трех точек
на прямой только одна лежит между двумя другими.
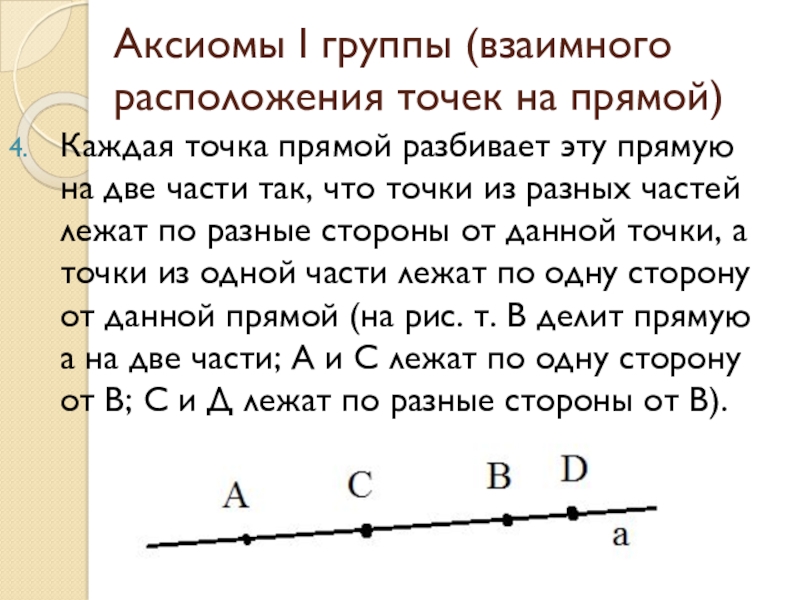
Слайд 7Аксиомы I группы (взаимного расположения точек на прямой)
Каждая точка прямой разбивает
эту прямую на две части так, что точки из разных частей лежат по разные стороны от данной точки, а точки из одной части лежат по одну сторону от данной прямой (на рис. т. В делит прямую а на две части; А и С лежат по одну сторону от В; С и Д лежат по разные стороны от В).
Слайд 8Опр. Часть прямой, состоящая из двух данных точек и всех точек,
лежащих между ними, называются отрезком. При этом сами данные точки называются концами отрезка.
Отрезок обозначается указанием его концов: AB, BC и т.д. Там где это не вызывает недоразумений, будем обозначать отрезки малыми латинскими буквами: a, b, c и т.д.
Отрезок обозначается указанием его концов: AB, BC и т.д. Там где это не вызывает недоразумений, будем обозначать отрезки малыми латинскими буквами: a, b, c и т.д.
Слайд 9Аксиомы I группы
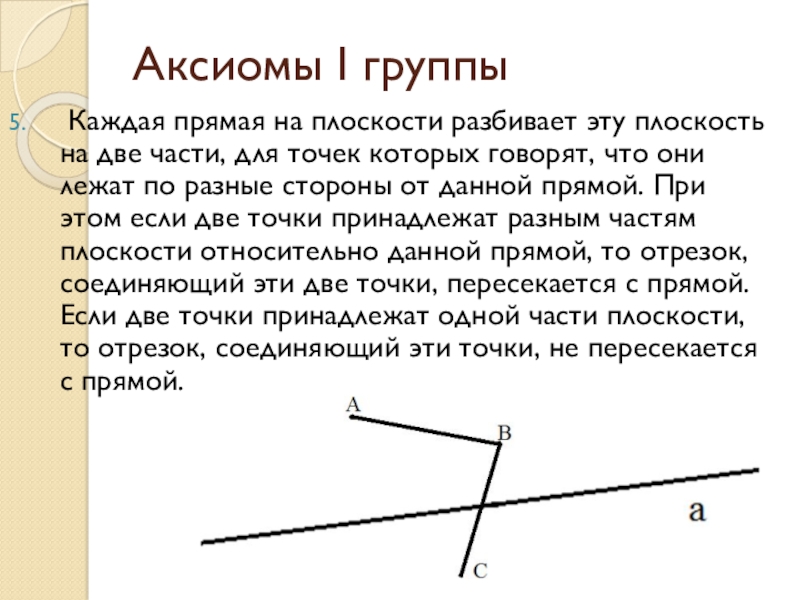
Каждая прямая на плоскости разбивает эту плоскость на
две части, для точек которых говорят, что они лежат по разные стороны от данной прямой. При этом если две точки принадлежат разным частям плоскости относительно данной прямой, то отрезок, соединяющий эти две точки, пересекается с прямой. Если две точки принадлежат одной части плоскости, то отрезок, соединяющий эти точки, не пересекается с прямой.
Слайд 10Опр. Часть прямой, состоящая из данной точки и всех точек, лежащих
от нее по одну сторону, называется полупрямой или лучом. При этом сама данная точка называется началом или вершиной луча.
Для обозначения лучей используются пары больших латинских букв, например, AB, первая из которых обозначает начало луча, а вторая – какую-нибудь точку, принадлежащую лучу.
Для обозначения лучей используются пары больших латинских букв, например, AB, первая из которых обозначает начало луча, а вторая – какую-нибудь точку, принадлежащую лучу.
Слайд 11 Одной из основных операций, которую можно производить с отрезками, является операция
откладывания данного отрезка на данном луче от его вершины. Получающийся при этом отрезок называется равным исходному.
Слайд 12Опр. Если на отрезке АВ между точками А и В взять
какую-либо точку С, то образуется два новых отрезка АС и СВ. Отрезок АВ называется суммой отрезков АС и СВ и обозначается
АВ = АС + СВ. Каждый из отрезков АС и СВ называется разностью отрезка АВ и другого отрезка и обозначается
АС = АВ - СВ, СВ = АВ - АС.
АВ = АС + СВ. Каждый из отрезков АС и СВ называется разностью отрезка АВ и другого отрезка и обозначается
АС = АВ - СВ, СВ = АВ - АС.
Слайд 13 Чтобы сложить два произвольных отрезка AB и CD, продолжим отрезок АВ
за точку В и на этом продолжении отложим отрезок ВЕ, равный CD. Отрезок АЕ даст сумму отрезков AB и CD, АЕ = AB + CD. Аналогичным образом поступают для вычитания из большего отрезка меньшего.
Слайд 14 Используя операцию сложения отрезка с самим собой, можно определить операцию умножения
отрезка на натуральное число. А именно для отрезка АВ положим: 2АВ=АВ+АВ, 3АВ=2АВ+АВ, …,
nАВ = (n-1)АВ+АВ, … .
Определим также операцию деления отрезка на n (n - натуральное число) равных частей, считая АВ : n отрезком, при умножении которого на n получается исходный отрезок АВ, т.е. n· (AB : n) = AB.
nАВ = (n-1)АВ+АВ, … .
Определим также операцию деления отрезка на n (n - натуральное число) равных частей, считая АВ : n отрезком, при умножении которого на n получается исходный отрезок АВ, т.е. n· (AB : n) = AB.
Слайд 15Аксиомы II группы (относятся к понятию равенства отрезков)
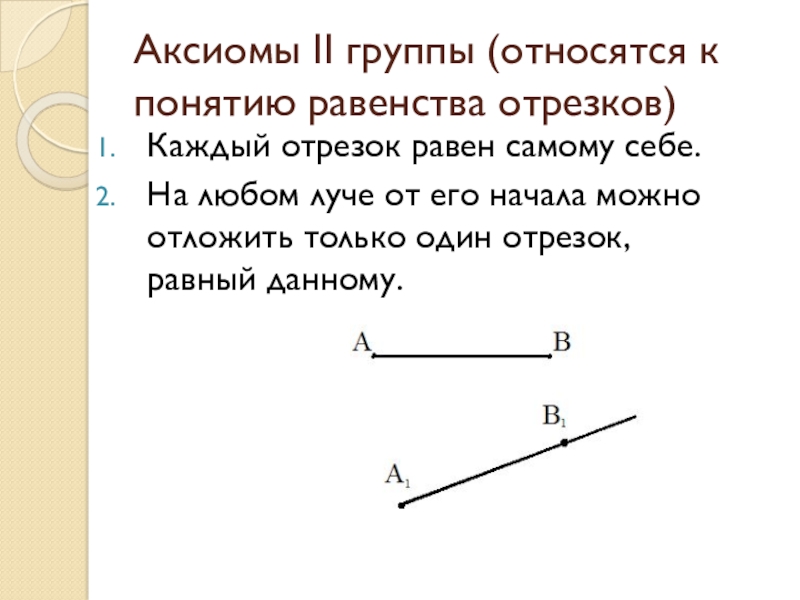
Каждый отрезок равен самому
себе.
На любом луче от его начала можно отложить только один отрезок, равный данному.
На любом луче от его начала можно отложить только один отрезок, равный данному.
Слайд 16Аксиомы II группы
Два отрезка, равные третьему, равны между собой.
Отрезки, полученные сложением
или вычитанием равных отрезков, равны.
Каждый отрезок можно разделить на n равных частей, n = 2, 3, … .
Каждый отрезок можно разделить на n равных частей, n = 2, 3, … .
Слайд 17Опр. Фигура, образованная двумя лучами с общей вершиной и одной из
частей плоскости, ограниченной этими лучами, называется углом. Общая вершина называется вершиной угла, а сами лучи – сторонами угла.
Опр. Угол называется развернутым, если его лучи вместе составляют прямую. В противном случае угол называется неразвернутым.
Опр. Угол называется развернутым, если его лучи вместе составляют прямую. В противном случае угол называется неразвернутым.
Слайд 18 Одной из основных операций, которую можно производить с углами, является операция
откладывания данного угла в ту или другую сторону от данного луча. Получающийся при этом угол называется равный исходному углу. Равенство углов АОВ и А1О1В1 записывается в виде АОВ = А1О1В1 . Оно означает, что если один из этих углов, например АОВ, отложить от луча О1А1 в сторону, определяемую лучом О1В1 , то АОВ при этом совместится с А1О1В1.
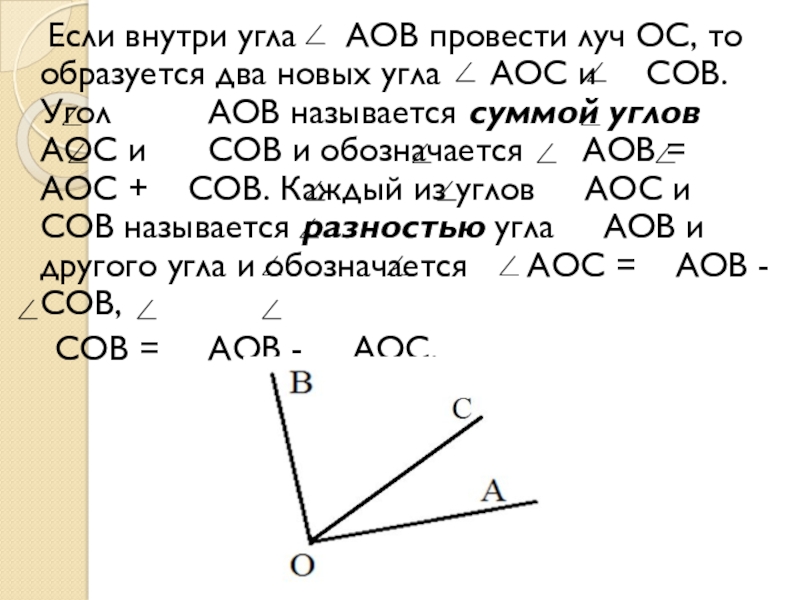
Слайд 19 Если внутри угла АОВ провести луч ОС, то образуется
два новых угла АОС и СОВ. Угол АОВ называется суммой углов АОС и СОВ и обозначается АОВ = АОС + СОВ. Каждый из углов АОС и СОВ называется разностью угла АОВ и другого угла и обозначается АОС = АОВ - СОВ,
СОВ = АОВ - АОС.
СОВ = АОВ - АОС.
Слайд 20Аксиомы III группы (равенство углов)
Каждый угол равен самому себе.
От любого луча
на плоскости в заданную сторону можно отложить только один угол, равный данному.
Два угла, равные третьему, равны между собой.
Углы, полученные сложением или вычитанием равных углов равны.
Каждый угол можно разделить на n равных частей, n = 2, 3, … .
Все развернутые углы равны.
Два угла, равные третьему, равны между собой.
Углы, полученные сложением или вычитанием равных углов равны.
Каждый угол можно разделить на n равных частей, n = 2, 3, … .
Все развернутые углы равны.
Слайд 21Опр. Фигура, образованная простой замкнутой ломаной и ограниченной ею частью плоскости,
называется многоугольником. Вершины ломаной называются вершинами многоугольника, стороны ломаной – сторонами многоугольника, а углы, образованные соседними сторонами, – углами многоугольника. Многоугольник с тремя углами называется треугольником.
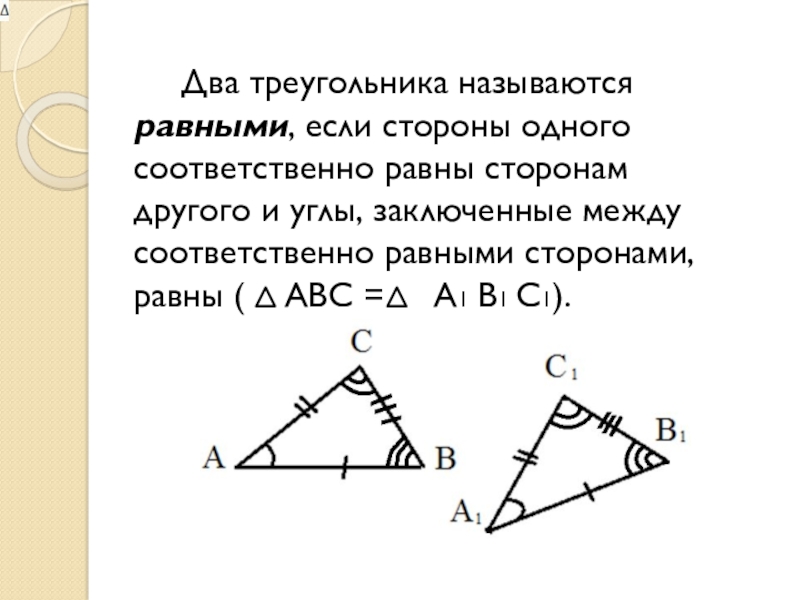
Слайд 22 Два треугольника называются равными, если стороны одного соответственно равны сторонам другого
и углы, заключенные между соответственно равными сторонами, равны ( ABC = A1 B1 C1).
Слайд 23Аксиома IV группы
В заданной полуплоскости относительно заданного луча можно отложить треугольник,
равный данному.
Слайд 24Опр. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, одинаково
удаленных от данной точки. Эта точка называется центром окружности. Расстояние от точек окружности до ее центра называется радиусом окружности.
Опр. Если две окружности имеют две общие точки, то они пересекаются.
Опр. Если две окружности имеют две общие точки, то они пересекаются.
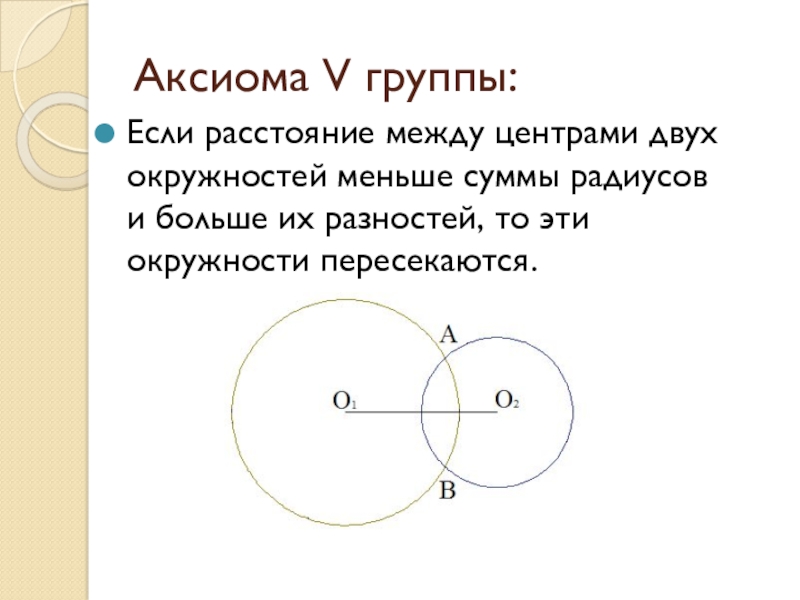
Слайд 25Аксиома V группы:
Если расстояние между центрами двух окружностей меньше суммы радиусов
и больше их разностей, то эти окружности пересекаются.
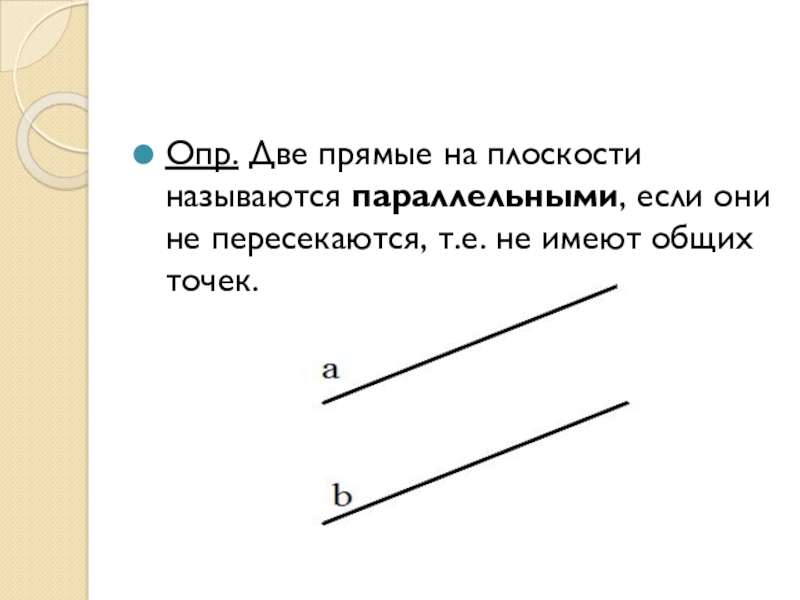
Слайд 26Опр. Две прямые на плоскости называются параллельными, если они не пересекаются,
т.е. не имеют общих точек.
Слайд 27Аксиома VI группы (аксиома параллельных)
Через точку, не лежащую на данной прямой,
проходит не более одной прямой, параллельной данной.
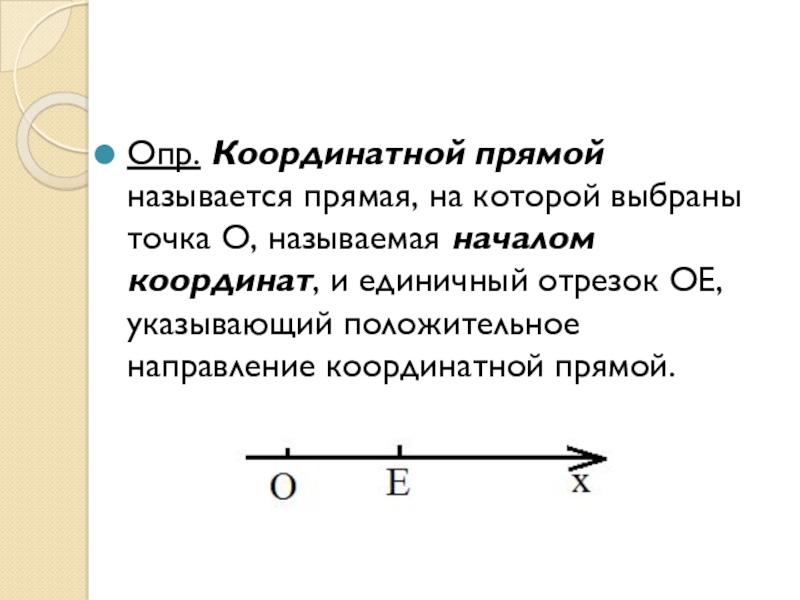
Слайд 28Опр. Координатной прямой называется прямая, на которой выбраны точка О, называемая
началом координат, и единичный отрезок ОЕ, указывающий положительное направление координатной прямой.
Слайд 29Опр. Координатой точки А на координатной прямой называется число x, равное
расстоянию от точки А до начала координат О, взятому со знаком «+», если А принадлежит положительной полуоси, и со знаком «-», если А принадлежит отрицательной полуоси.
Слайд 30Аксиома VII группы (аксиома непрерывности)
Соответствие, при котором точкам координатной прямой
сопоставляются их координаты, является взаимно однозначным соответствием между точками координатной прямой и действительными числами.
Слайд 31Это означает, что каждой точке координатной прямой соответствует единственное число и
каждому числу соответствует единственная точка на координатной прямой. Такое соответствие позволяет дать геометрическую интерпретацию действительных чисел, изображая их точками на координатной прямой.
Слайд 32Аксиомы VIII группы (аксиомы стереометрии)
Через любые две точки пространства проходит единственная
прямая.
Слайд 33Аксиомы VIII группы (аксиомы стереометрии):
Через любые три точки пространства, не лежащие
на одной прямой, проходит единственная плоскость.
Слайд 34Аксиомы VIII группы (аксиомы стереометрии):
Если две плоскости имеют общую точку, то
они пересекаются по прямой.
Слайд 35Аксиомы VIII группы (аксиомы стереометрии)
Существуют по крайней мере четыре точки, не
принадлежащие одной плоскости.
Слайд 36Опр. Два угла называются вертикальными, если стороны одного угла дополняют до
прямых стороны другого угла ( AOC и BOD ).
Опр. Два угла называются смежными, если одна сторона у них общая , а две другие составляют вместе прямую ( AOC и COB).
Опр. Два угла называются смежными, если одна сторона у них общая , а две другие составляют вместе прямую ( AOC и COB).
Слайд 37Дано: AOC и BOD – вертикальные углы.
Док-ть:
AOC = BOD.
Док-во. Стороны OB и OD BOD дополняют до прямых стороны OA и OC AOC. Тогда углы AOC и COB составляют в сумме развернутый угол. Углы BOD и COB также составляют в сумме развернутый угол. Поскольку все развернутые углы равны, то имеем равенство
AOC + COB = BOD + COB. Вычитая из обеих частей этого равенства COB, получаем требуемое равенство AOC = BOD.
Док-во. Стороны OB и OD BOD дополняют до прямых стороны OA и OC AOC. Тогда углы AOC и COB составляют в сумме развернутый угол. Углы BOD и COB также составляют в сумме развернутый угол. Поскольку все развернутые углы равны, то имеем равенство
AOC + COB = BOD + COB. Вычитая из обеих частей этого равенства COB, получаем требуемое равенство AOC = BOD.
Теорема. Вертикальные углы равны.