- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Квадрат теңдеу 8 сынып
Содержание
- 1. Квадрат теңдеу 8 сынып
- 2. Сабақтан қалмай, сапалы да,саналы білім алу
- 3. Сабақ мақсаты:Біліктілік: Квадраттық теңдеулерді формула көмегімен шығаруды
- 4. Сабақтың барысы
- 5. Қайталау сұрақтарыҚандай теңдеуді квадраттық теңдеу деп атайды?2.
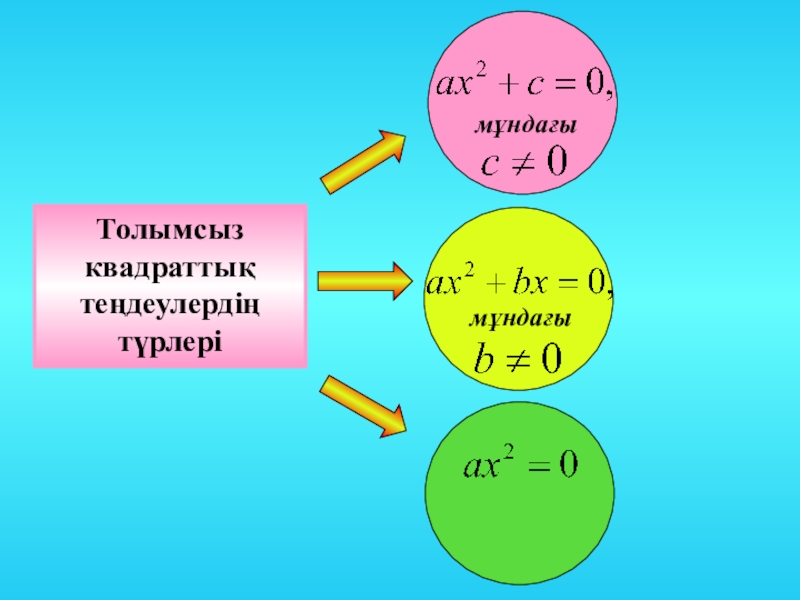
- 6. Толымсыз квадраттық теңдеулердің түрлері
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. теңдеуі теңдеуімен мәндес. Мұның түбірлерінің саны
- 11. -ға тәуелді мүмкін
- 12. Сонымен, бұл жағдайда
- 13. 2. Егер
- 14. 3. Егер
- 15. 1-мысал
- 16. 2-мысал
- 17. 3-мысалЖауабы: түбірлері жоқ.
- 18. Есеп №1.
- 19. Есеп №2.Түбірлерсаны
- 20. Деңгейлік тапсырмаларС үшмүшесі 1-ге тең мән қабылдайды.ВВ Ах-тің қандай мәндеріндекөпмүшелерінің мәндері тең болады.және
- 21. Тест тапсырмалары1. Теңдеуді шешіңіз:2. Теңдеуді шешіңіз:3. Теңдеуді шешіңіз:4. Теңдеуді шешіңіз:5. Теңдеуді шешіңіз:6. Теңдеуді шешіңіз:
- 22. Тест тапсырмалары1. Теңдеуді шешіңіз:2. Теңдеуді шешіңіз:3. Теңдеуді шешіңіз:4. Теңдеуді шешіңіз:5. Теңдеуді шешіңіз:6. Теңдеуді шешіңіз:
- 23. Барлық рационал және иррационал сандардан тұратын сандар
- 24. Үйге тапсырма:№260, №261.Ш ы ғ у
- 25. түріндегі теңдеуді квадрат теңдеу деп атайды. Мұнда
- 26. Мұнда а – квадрат теңдеудің бірінші коэффициенті,
- 27. Квадрат теңдеулердің дербес жағдайларында b немесе с,
- 28. екі түбірі бар, олардың біреуі нөлге тең.екі түбірі бар немесе шешімі жоқбір түбірі бар
- 29. Назарларыңызға рахмет!
Слайд 3Сабақ мақсаты:
Біліктілік: Квадраттық теңдеулерді формула көмегімен шығаруды үйрету, толымсыз квадраттық теңдеулер
Дамытушылық: Оқушылардың ақыл-ойын дамыту, ойлау қабілетін жетілдіру, есеп шығарудың жаңа түрлерін меңгерту және ойдан ой туындатуға, әр сөзді, айтылған ойды дәлелдеуге үйрету.
Тәрбиелік: Оқушылардың алгебра пәніне қызығушылығын арттыру, оқушыларды алғырлыққа, шапшаңдыққа тәрбиелеу.
Слайд 5Қайталау сұрақтары
Қандай теңдеуді квадраттық теңдеу деп атайды?
2. Квадраттық теңдеудегі a, b,
3. Қандай теңдеуді толымсыз квадраттық теңдеу деп атайды?
4. Толымсыз квадраттық теңдеудің әр түрінің неше түбірі бар болады?
Слайд 9
Осы теңдеуді түрлендірейік:
Слайд 10теңдеуі
теңдеуімен
мәндес. Мұның түбірлерінің саны
бөлшегінің
таңбасына тәуелді болады.
болғандықтан,
- оң сан болады, сондықтан бұл бөлшектің
таңбасы оның алымының, яғни өрнегінің таңбасымен
анықталады. Осы өрнекті квадраттық
теңдеуінің дискриминанты деп атайды. Мұны D әрпімен
белгілейді, яғни Енді екінші теңдеуді
мына түрде жазамыз:
Слайд 12Сонымен, бұл жағдайда
Қысқаша былай жазуға болады:
мұны квадраттық теңдеудің түбірлерінің формуласы деп атайды.
мұндағы
Слайд 143. Егер болса,
болады, сондықтан
теңдеуінің түбірлері жоқ.
Онда теңдеудің де түбірлері жоқ болады.
Сонымен,
екі түбірі болады
бір түбір болады
түбірлері жоқ
Слайд 20Деңгейлік тапсырмалар
С
үшмүшесі 1-ге тең мән қабылдайды.
В
В
А
х-тің қандай мәндерінде
көпмүшелерінің мәндері
және
Слайд 21Тест тапсырмалары
1. Теңдеуді шешіңіз:
2. Теңдеуді шешіңіз:
3. Теңдеуді шешіңіз:
4. Теңдеуді шешіңіз:
5. Теңдеуді
6. Теңдеуді шешіңіз:
Слайд 22Тест тапсырмалары
1. Теңдеуді шешіңіз:
2. Теңдеуді шешіңіз:
3. Теңдеуді шешіңіз:
4. Теңдеуді шешіңіз:
5. Теңдеуді
6. Теңдеуді шешіңіз:
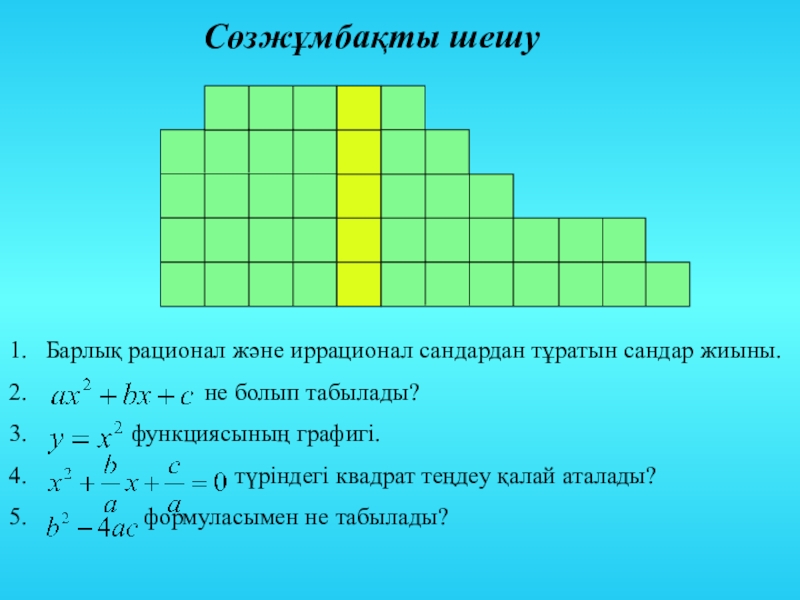
Слайд 23Барлық рационал және иррационал сандардан тұратын сандар жиыны.
функциясының графигі.
түріндегі квадрат теңдеу қалай аталады?
формуласымен не табылады?
Сөзжұмбақты шешу
Слайд 25
түріндегі теңдеуді квадрат теңдеу деп атайды.
Мұнда a, b және с
ал х – айнымалы.
Анықтама.
Слайд 26
Мұнда а – квадрат теңдеудің бірінші коэффициенті, b – екінші коэффициенті,
Слайд 27
Квадрат теңдеулердің дербес жағдайларында b немесе с, немесе екеуі бірдей нөлге
Бұларды толымсыз квадрат теңдеулер деп атайды.