Исследовательская работа обучающейся 8 «А» класса
МКОУ « Верхнехавская средняя общеобразовательная школа № 1»
Меркушовой Анастасии
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследовательская работа по математике Лист Мёбиуса (презентация)
Содержание
- 1. Исследовательская работа по математике Лист Мёбиуса (презентация)
- 2. Значок механико-математического факультета МГУ
- 3. компьютерный салонмеждународный символ повторного использования
- 4. Фотография памятника, поставленного во Франкфурте-на-Майне
- 5. Памятник в Минске (Беларусь) Скульптурная композиция перед
- 6. Памятник листуМёбиуса вМоскве околоКинотеатра «Горизонт»
- 7. Скульптура, украшающая окрестности здания центра физических исследований в американском штате Иллинойс.
- 8. Невероятный проект новой библиотеки в Астане
- 9. В 1967 году, когда
- 10. Август Фердинанд Мёбиус (1790-1868)Таинственный и знаменитый лист
- 11. Изготовление листа (ленты) Мёбиуса. Смотрите, я беру
- 12. Слайд 12
- 13. Лист (лента) Мёбиуса
- 14. Получили лист Мёбиуса -знаменитое в математике перекрученное кольцо.
- 15. Легко убедиться, что у ленты Мёбиуса только одна сторона
- 16. Закрашенной оказалась вся лента целиком! А
- 17. Покажется, что распростерлась Вечность, Что взломан Мироздания
- 18. Лист Мёбиуса обладает любопытными свойствами. Он
- 19. Афганская лента
- 20. Если разрезать новую ленту Мёбиуса на расстояние
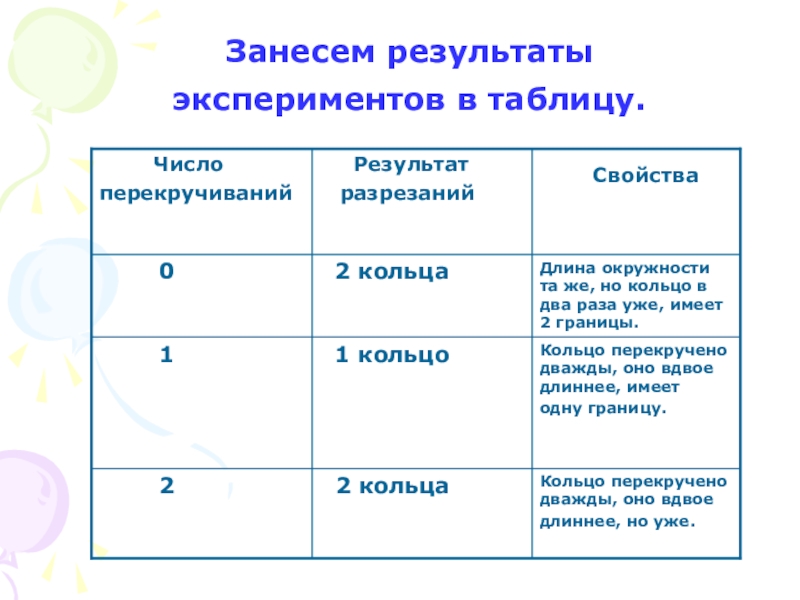
- 21. Занесем результаты экспериментов в таблицу.
- 22. Лист Мёбиуса в форме трилистника
- 23. Интересные свойства ленты Мёбиуса привлекли внимание не только математиков, но и фокусников.
- 24. Топология изучает свойства тел и поверхностей пространства, которые не изменяются при деформации,
- 25. Топологические свойства листа Мёбиуса1.Односторонность – топологическое свойство
- 26. Морис Эшер (1898-1972).
- 27. Можно встретить множество настольных композиций ленты Мёбиуса.
- 28. Не обошли своим вниманием знаменитый лист Мёбиуса и ювелиры.
- 29. Лист Мёбиуса постоянно встречается в научной фантастике
- 30. Иногда научно - фантастические рассказы (вслед
- 31. Есть гипотеза, что спираль ДНК сама по
- 32. Лист Мёбиуса нашел применение и в кулинарии
- 33. А можно лист Мёбиуса и связать.
- 34. На фотографии мы видим футболку с аппликацией. На аппликации ,знакомый нам, лист Мёбиуса.
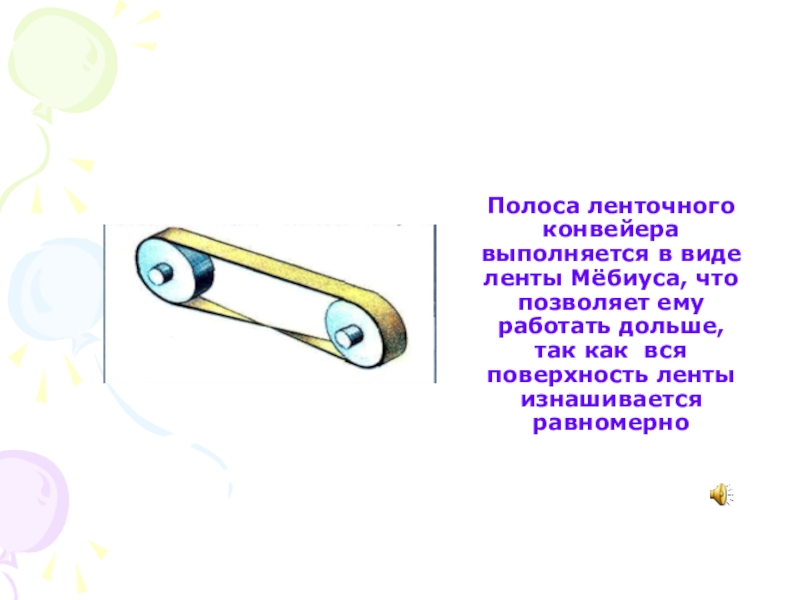
- 35. Полоса ленточного конвейера выполняется в виде ленты
- 36. Конечно же, главная ценность листа Мёбиуса
- 37. Лист Мёбиуса - первая односторонняя поверхность, которую
- 38. Многие поэты посвящают стихи листу Мёбиуса
Слайд 1 Лист Мёбиуса
Слайд 5Памятник в Минске (Беларусь)
Скульптурная композиция перед Центральной научной библиотекой имени
Слайд 7Скульптура, украшающая окрестности здания
центра физических исследований в американском штате Иллинойс.
Слайд 8Невероятный проект новой библиотеки
в Астане (Казахстан)
Проект здания площадью 33 тыс.
Слайд 9 В 1967 году, когда в Бразилии состоялся международный
Слайд 10Август Фердинанд Мёбиус (1790-1868)
Таинственный и знаменитый лист
Мебиуса (иногда говорят: "лента
придумал в 1858 г. немецкий геометр
Август Фердинанд Мёбиус (1790-1868),
ученик "короля математиков" Гаусса.
Мёбиус был первоначально астрономом,
как Гаусс и многие другие из тех, кому
математика была обязана своим развитием.
В те времена занятия математикой
не встречали поддержки, а астрономия
давала достаточно денег, чтобы не думать
о них, и оставляла время для собственных
размышлений. Мёбиус стал одним из
крупнейших геометров XIX в.
В возрасте 68 лет ему удалось сделать
открытие поразительной красоты.
Это открытие односторонних
поверхностей, одна из которых - лист Мёбиуса.
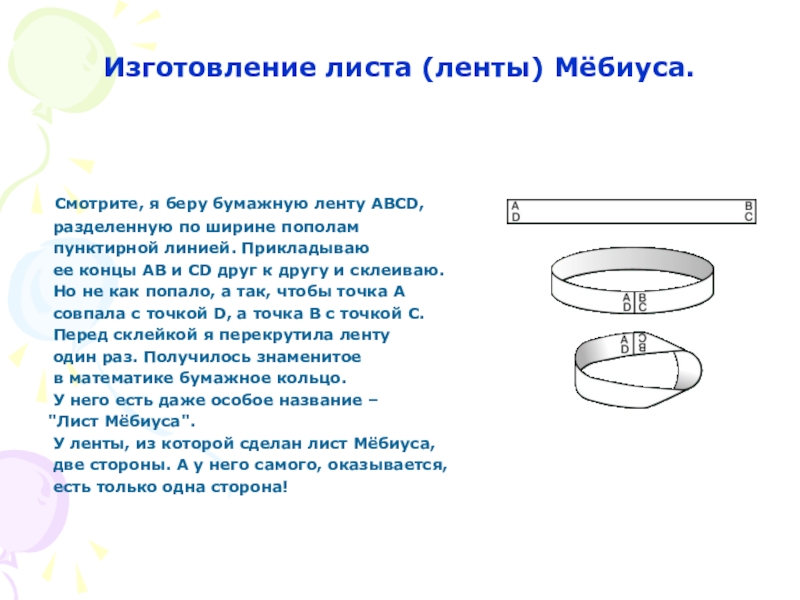
Слайд 11Изготовление листа (ленты) Мёбиуса.
Смотрите, я беру бумажную ленту АВСD,
разделенную
пунктирной линией. Прикладываю
ее концы АВ и СD друг к другу и склеиваю.
Но не как попало, а так, чтобы точка А
совпала с точкой D, а точка B с точкой С.
Перед склейкой я перекрутила ленту
один раз. Получилось знаменитое
в математике бумажное кольцо.
У него есть даже особое название –
"Лист Мёбиуса".
У ленты, из которой сделан лист Мёбиуса,
две стороны. А у него самого, оказывается,
есть только одна сторона!
Слайд 16 Закрашенной оказалась вся лента целиком! А ведь мы ее не
Слайд 17Покажется, что распростерлась Вечность, Что взломан Мироздания пароль. И вдруг твое стремленье в
Слайд 18 Лист Мёбиуса обладает любопытными свойствами. Он преподнесет вам сюрприз, если вы
Слайд 20Если разрезать новую ленту Мёбиуса на расстояние 1/3 ее ширины от
Слайд 23Интересные свойства ленты Мёбиуса привлекли внимание не только математиков, но и
Слайд 24Топология изучает свойства тел и поверхностей пространства, которые не изменяются при деформации, например, растяжении, сжатии или
Слайд 25Топологические свойства листа Мёбиуса
1.Односторонность – топологическое свойство листа Мебиуса, характерное для
2.Непрерывность – на листе Мёбиуса любая точка может быть соединена с любой другой точкой. Разрывов нет – непрерывность полная.
3.Связность – чтобы располовинить кольцо, потребуется два разреза. Что касается листа Мёбиуса, то количество связей изменяется в зависимости от смены количества оборотов ленты: если один оборот – двусвязен, если два оборота – односвязен, если три – двусвязен и т. д.
А вот чтобы разделить квадрат на две части, нам потребуется только один разрез.
Слайд 29Лист Мёбиуса постоянно встречается в научной фантастике
В рассказе «Лист Мёбиуса»
бостонское метро строит новую линию, маршрут которой становится настолько
запутанным, что
превращается в ленту Мёбиуса,
после чего на этой линии начинают исчезать поезда.
По мотивам рассказа был
снят фантастический
фильм «Мёбиус» режиссёра
Густаво Москера
Слайд 30Иногда научно - фантастические рассказы (вслед за физиками-теоретиками) предполагают, что наша
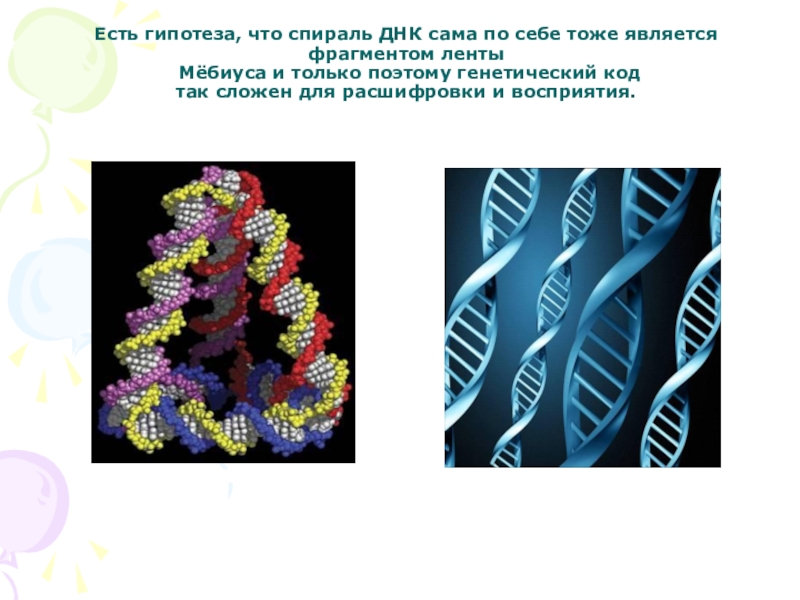
Слайд 31Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом
Слайд 35Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему
Слайд 36 Конечно же, главная ценность листа Мёбиуса состоит в том, что
Слайд 37Лист Мёбиуса - первая односторонняя поверхность, которую открыл учёный. Позже математики
Слайд 38 Многие поэты посвящают стихи листу Мёбиуса - уникальной односторонней поверхности.
Лист Мебиуса – символ математики,
Что служит высшей мудрости венцом…
Он полон неосознанной романтики:
В нем бесконечность свернута кольцом.
В нем – простота, и вместе с нею – сложность,
Что недоступна даже мудрецам:
Здесь на глазах преобразилась плоскость
В поверхность без начала и конца.