- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Интерактивная лекция Теория игр
Содержание
- 1. Интерактивная лекция Теория игр
- 2. Теория игр – это раздел математики, изучающий математические модели принятия решений в конфликтных ситуациях.
- 3. Теория игр опирается на предположение о том,
- 4. Жозеф Луи Франсуа Бертран французский математик 1.Профессор
- 5. Джон фон Нейман венгро-американский математик1)Профессор Принстонского университета
- 6. Джон Форбс Нэш американский математик 1.Лауреат Нобелевской
- 7. Дж. Нэш доказал, что классический подход к
- 8. Основное понятие теории игр - играИгра -
- 9. От реального конфликта игра отличается тем, что
- 10. АНТАГОНИЗМ — (от греч. antahonisma спор, борьба)
- 11. Примеры конфликтных ситуацийвзаимоотношения покупателя и продавца конкуренция различных фирм боевые действия
- 12. А также обычные игры
- 13. Игроки – заинтересованные стороны в игре.Партия игры
- 14. Игра состоит из ходов, выполняемых игроками одновременно
- 15. Стратегией игрока называется совокупность правил, определяющих выбор
- 16. Стратегия игрока называется оптимальной, если она обеспечивает
- 17. Недостаток теории игрПредположение о полной (“идеальной”) разумности
- 18. Матричные игрыПусть в игре участвуют два игрока
- 19. Слайд 19
- 20. Оптимальной стратегией игрока в матричной игре называется
- 21. ПРИНЦИП МАКСМИНАнеобходимо выбрать ту стратегию, которая позволит при наихудшем поведении противника получить максимальный выигрыш.
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Игрок В гарантирует себе проигрыш не выше
- 26. Слайд 26
- 27. 1) Если v > 0, то игра
- 28. Если в игре нет седловой точки в
- 29. Смешанной стратегией игрока называются случайные величины, возможные значения которых являются чистые стратегии.
- 30. Слайд 30
- 31. Основная теорема матричных игрЛюбая матричная игра имеет,
- 32. Оптимальное решение игры в смешанных стратегиях обладает
- 33. Определение. Те из чистых стратегий игроков А
- 34. Условия применения смешанных стратегий1. Игра без седловой
- 35. Методы решение матричных игр в смешанных стратегиях 2х2АналитическийметодГрафическийметод
- 36. Слайд 36
- 37. В соответствии с теоремой об активных стратегиях,
- 38. Слайд 38
- 39. Eсли игрок А использует свою оптимальную смешанную
- 40. ЗАДАНИЕ
- 41. Сначала необходимо определить, решается ли данная игра
- 42. Каждый из игроков А и В обладает единственной оптимальной смешанной стратегией
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
- 49. . Решить матричную игру аналитическим и графическим способом
Теория игр – это раздел математики, изучающий математические модели принятия решений в конфликтных ситуациях.
Слайд 2
Теория игр – это раздел математики, изучающий математические модели принятия решений
в конфликтных ситуациях.
Слайд 3
Теория игр опирается на предположение о том, что независимо от цели
игры и ее обстоятельств найдется стратегия, которая позволит добиться успеха.
это всегда происходит по определенным правилам, но иногда их трудно распознать
Слайд 4Жозеф Луи Франсуа Бертран
французский математик
1.Профессор Политехнической школы и Колледжа
Франции, член Парижской академии наук.
2.Работал в области теории чисел, дифференциальной геометрии, теории вероятности и термодинамики.
3.Дал математическую трактовку стратегии в играх в курсе теории вероятностей «Calcul des probabilités» в 1889 г.
2.Работал в области теории чисел, дифференциальной геометрии, теории вероятности и термодинамики.
3.Дал математическую трактовку стратегии в играх в курсе теории вероятностей «Calcul des probabilités» в 1889 г.
Слайд 5
Джон фон Нейман
венгро-американский математик
1)Профессор Принстонского университета США.
2) Сотрудник RAND
Corporation (американский стратегический центр для обеспечения национальной безопасности страны).
3)Внес большой вклад в создание первых ЭВМ и разработку методов их применения. 2) Важную роль в экономике сыграла теория игр, разработанная Нейманом и О. Моргенштерном
3)Внес большой вклад в создание первых ЭВМ и разработку методов их применения. 2) Важную роль в экономике сыграла теория игр, разработанная Нейманом и О. Моргенштерном
Слайд 6
Джон Форбс Нэш американский математик
1.Лауреат Нобелевской премии по экономике 1994
года «За анализ равновесия в теории некооперативных игр».
2.Сотрудник RAND Corporation.
3.Работал в Принстоне и Массачусетском технологическом институте, получил звание профессора Принстонского университета
2.Сотрудник RAND Corporation.
3.Работал в Принстоне и Массачусетском технологическом институте, получил звание профессора Принстонского университета
Слайд 7
Дж. Нэш доказал, что классический подход к конкуренции А.Смита, когда каждый
сам за себя, неоптимален.
Наиболее оптимальны те стратегии, при которых каждый старается сделать лучше для себя, делая лучше для других.
Наиболее оптимальны те стратегии, при которых каждый старается сделать лучше для себя, делая лучше для других.
Слайд 8
Основное понятие теории игр - игра
Игра - упрощенная модель реальной конфликтной
ситуации.
Цель теории игр - выработка рекомендаций по разумному поведению участников конфликта (определение оптимальных стратегий поведения игроков).
Слайд 9От реального конфликта игра отличается тем, что ведется по определенным правилам:
1.Правила устанавливают последовательность ходов, объем информации каждой стороны о поведении другой и результат игры в зависимости от сложившейся ситуации.
2.Правилами устанавливаются также конец игры, когда некоторая последовательность ходов уже сделана, и больше ходов делать не разрешается.
Слайд 10
АНТАГОНИЗМ — (от греч. antahonisma спор, борьба) противоречие, для которого характерна
острая непримиримая борьба враждующих сил, тенденций.
Слайд 11Примеры конфликтных ситуаций
взаимоотношения покупателя и продавца
конкуренция различных фирм
боевые действия
Слайд 13
Игроки – заинтересованные стороны в игре.
Партия игры – каждый конкретный пример
разыгрывания игры некоторым конкретным образом от начала до конца.
Ход игрока – выбор и осуществление действия производимого одним игроком в условиях точно определенных правилами игры.
Ход игрока – выбор и осуществление действия производимого одним игроком в условиях точно определенных правилами игры.
Слайд 14
Игра состоит из ходов, выполняемых игроками одновременно или последовательно.
личный
случайный
(ход, который игрок сознательно выбирает из совокупности возможных вариантов действий и осуществляет его)
ход выбор которого производится не
игроком, а каким-либо механизмом
случайного выбора
Слайд 15
Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом
личном ходе в зависимости от ситуации, сложившейся в процессе игры.
В простых (одноходовых) играх, когда в каждой партии игрок может сделать лишь по одному ходу, понятие стратегии и возможного варианта действий совпадают.
Слайд 16
Стратегия игрока называется оптимальной, если она обеспечивает данному игроку при многократном
повторении игры максимально возможный средний выигрыш или минимально возможный средний проигрыш, независимо от того, какие стратегии применяет противник.
Слайд 17
Недостаток теории игр
Предположение о полной (“идеальной”) разумности противников.
В реальном конфликте
зачастую оптимальная стратегия состоит в том, чтобы угадать, в чем слабость противника и воспользоваться этой слабостью
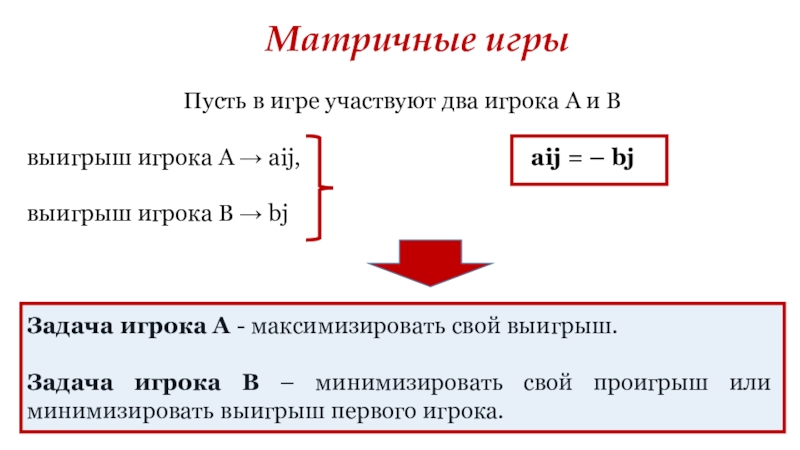
Слайд 18Матричные игры
Пусть в игре участвуют два игрока А и В
выигрыш игрока А → аij, аij = – bj
выигрыш игрока В → bj
Задача игрока А - максимизировать свой выигрыш.
Задача игрока В – минимизировать свой проигрыш или минимизировать выигрыш первого игрока.
Слайд 20
Оптимальной стратегией игрока в матричной игре называется такая, которая обеспечивает ему
максимальный выигрыш.
Задача каждого из игроков – найти наилучшую стратегию игры
Задача каждого из игроков – найти наилучшую стратегию игры
Слайд 21
ПРИНЦИП МАКСМИНА
необходимо выбрать ту стратегию, которая позволит при наихудшем поведении противника
получить максимальный выигрыш.
Слайд 25Игрок В гарантирует себе проигрыш не выше β.
Величина β называется
верхней ценой игры (минимаксом).
Для матричной игры всегда справедливо неравенство α≤β
Если α = β, то ситуация является равновесной. И такая игра называется игрой с седловой точкой. А пара оптимальных стратегий (Аопт, Вопт ) – седловой точкой матрицы.
Если α < β, то игра не имеет седловой точки.
а ij = α = β = ν, где ν называется ценой игры и является
одновременно минимальным в i-й строке и j-
м столбце. ν - решение матричной игры
Для матричной игры всегда справедливо неравенство α≤β
Если α = β, то ситуация является равновесной. И такая игра называется игрой с седловой точкой. А пара оптимальных стратегий (Аопт, Вопт ) – седловой точкой матрицы.
Если α < β, то игра не имеет седловой точки.
а ij = α = β = ν, где ν называется ценой игры и является
одновременно минимальным в i-й строке и j-
м столбце. ν - решение матричной игры
Слайд 271) Если v > 0, то игра выгодна для игрока А.
2)
Если v < 0 - для игрока В.
3) Если v = 0 - игра справедлива, т.е. является одинаково
выгодной для обоих участников
Применение максиминного принципа каждым из игроков обеспечивает:
- игроку А выигрыш не менее α,
- игроку В проигрыш не больше β.
Учитывая что α<β, целью игрока А будет - увеличение выигрыша, а для игрока В - уменьшение проигрыша.
3) Если v = 0 - игра справедлива, т.е. является одинаково
выгодной для обоих участников
Применение максиминного принципа каждым из игроков обеспечивает:
- игроку А выигрыш не менее α,
- игроку В проигрыш не больше β.
Учитывая что α<β, целью игрока А будет - увеличение выигрыша, а для игрока В - уменьшение проигрыша.
Слайд 28Если в игре нет седловой точки в чистых
стратегиях, то можно найти
нижнюю и верхнюю
чистые цены этой игры, которые указывают, что
игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры,
и может быть уверен в получении выигрыша не меньше нижней цены игры.
Поиск такого решения приводит к необходимости
применять смешанные стратегии
чистые цены этой игры, которые указывают, что
игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры,
и может быть уверен в получении выигрыша не меньше нижней цены игры.
Поиск такого решения приводит к необходимости
применять смешанные стратегии
Слайд 29Смешанной стратегией игрока называются случайные величины, возможные значения которых являются чистые
стратегии.
Слайд 31Основная теорема матричных игр
Любая матричная игра имеет, по крайней мере, одно
оптимальное решение, в общем случае, в смешанных стратегиях и соответствующую цену v.
Цена игры v - средний выигрыш, приходящийся на
одну партию, - всегда удовлетворяет условию
α≤ν≤β, т.е. лежит между нижней и верхней ценами игры.
Цена игры v - средний выигрыш, приходящийся на
одну партию, - всегда удовлетворяет условию
α≤ν≤β, т.е. лежит между нижней и верхней ценами игры.
Слайд 32Оптимальное решение игры
в смешанных стратегиях обладает тем свойством, что каждый
из игроков не заинтересован в отходе
от своей оптимальной смешанной стратегии,
если его противник применяет свою оптимальную смешанную стратегию, так как это ему невыгодно.
от своей оптимальной смешанной стратегии,
если его противник применяет свою оптимальную смешанную стратегию, так как это ему невыгодно.
Слайд 33Определение. Те из чистых стратегий игроков А и В, которые входят
в их оптимальные смешанные стратегии с вероятностями, не равными нулю, называются активными стратегиями.
Слайд 34Условия применения смешанных стратегий
1. Игра без седловой точки.
2. Игроки используют случайную
смесь чистых стратегий с заданными вероятностями.
3. Игра повторяется многократно в сходных условиях.
4. При любом ходе ни один из игроков не информирован о стратегии другого игрока.
5. Допускается усреднение результатов игр.
3. Игра повторяется многократно в сходных условиях.
4. При любом ходе ни один из игроков не информирован о стратегии другого игрока.
5. Допускается усреднение результатов игр.
Слайд 37В соответствии с теоремой об активных стратегиях, оптимальная смешанная стратегия обладает
тем свойством, что обеспечивает игроку максимальный средний выигрыш, равный цене игры , независимо от того, какие действия предпринимает другой игрок, если тот не выходит за пределы своих активных стратегий.
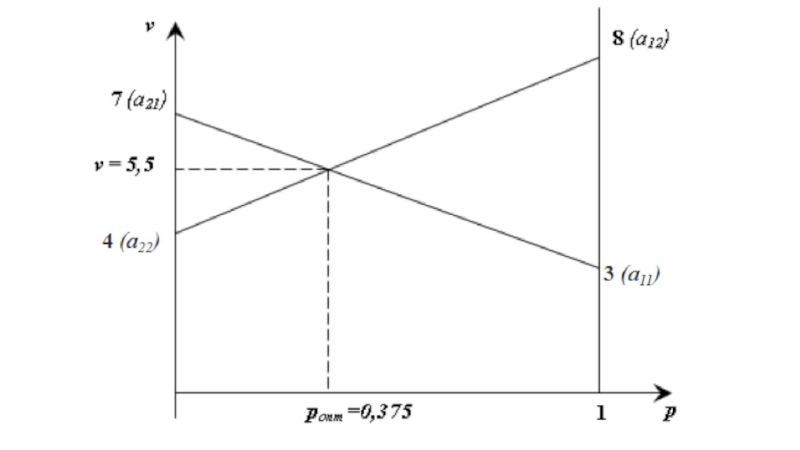
Слайд 39Eсли игрок А использует свою оптимальную смешанную стратегию, а игрок В
- свою чистую активную стратегию В 2 , то цена игры равна
Слайд 41
Сначала необходимо определить, решается ли данная игра в чистых стратегиях, то
есть существует ли седловая точка или нет.
7 8
