- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Электронный учебник: Свойства элементов треугольников
Содержание
- 1. Электронный учебник: Свойства элементов треугольников
- 2. Историческая справкаСвойства элементов треугольникаПримеры решения задачТест Опорные задачи
- 3. Историческая справка Треугольник-это простейшая фигура: три стороны и
- 4. Через площадь треугольника выражается площадь любого многоугольника:
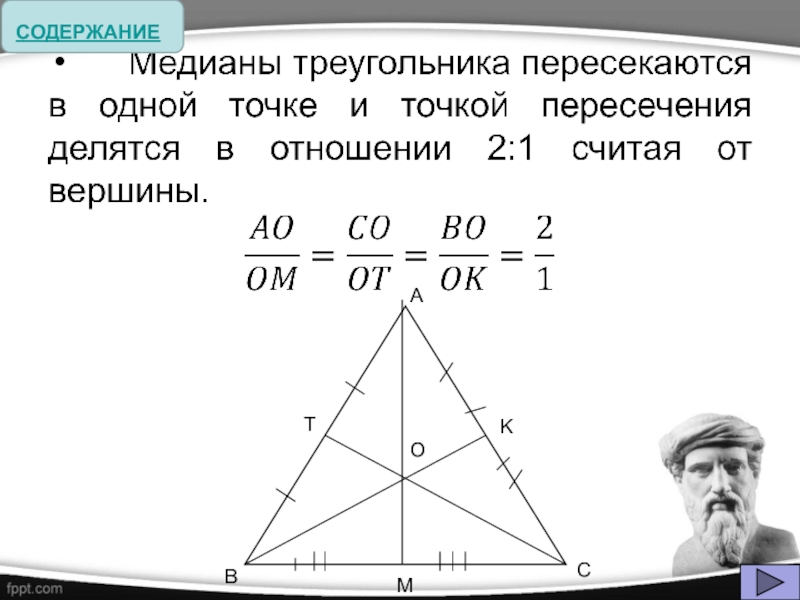
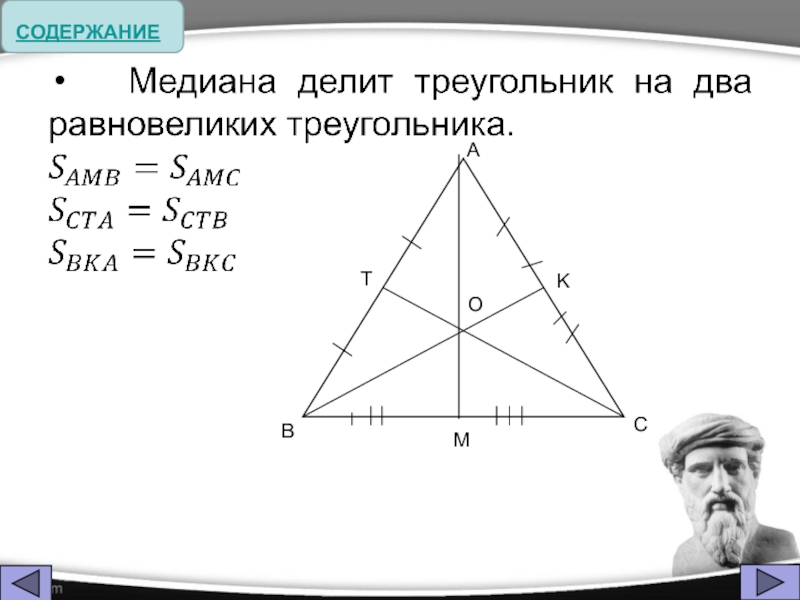
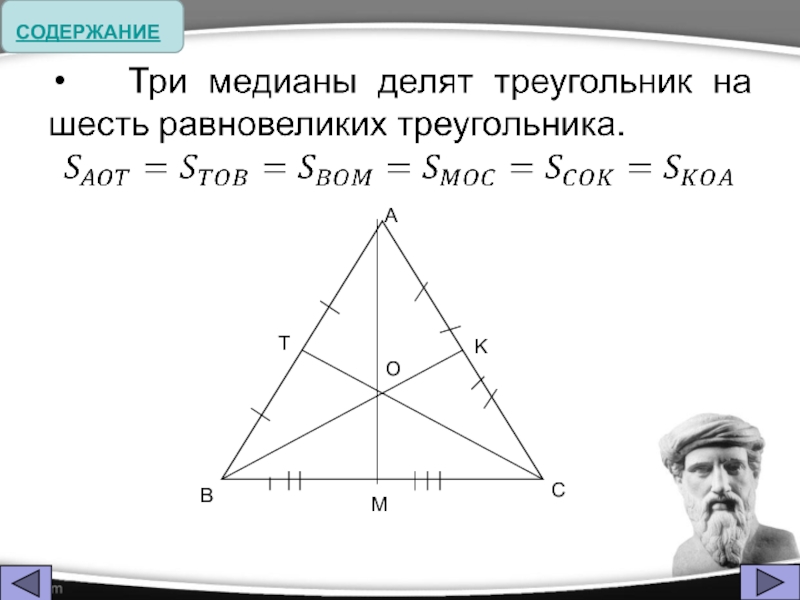
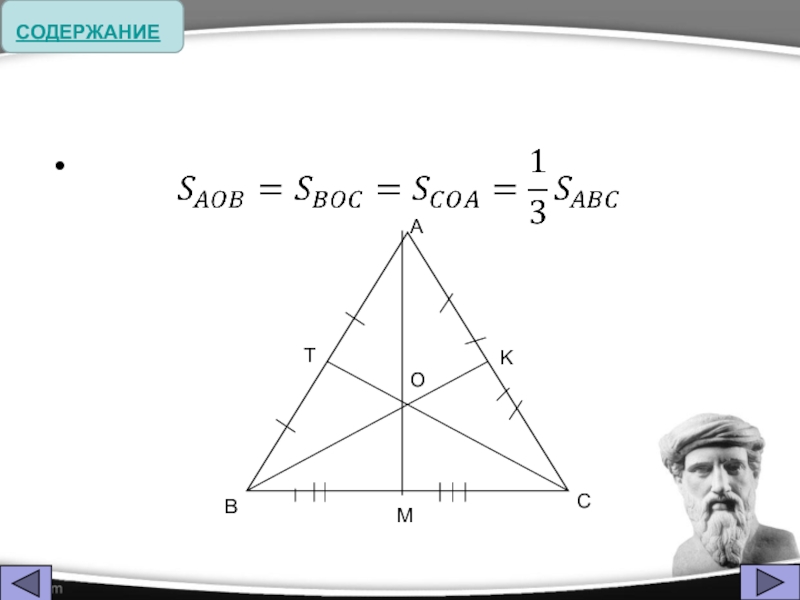
- 5. Термин «медиана» происходит от латинского слова mediana
- 6. SFNOPMH
- 7. Слайд 7
- 8. Биссектриса треугольника- это отрезок биссектрисы любого угла
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам AE:EC = AB:BC
- 22. Слайд 22
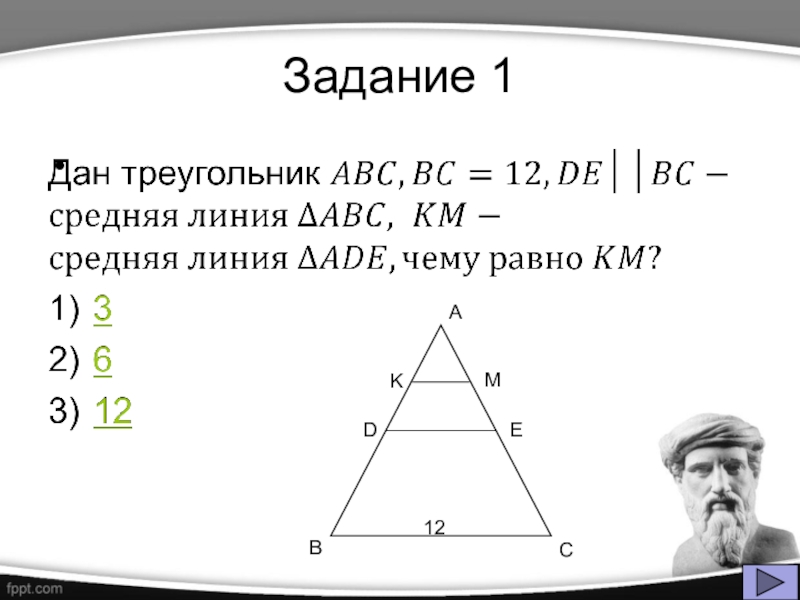
- 23. Задание 1
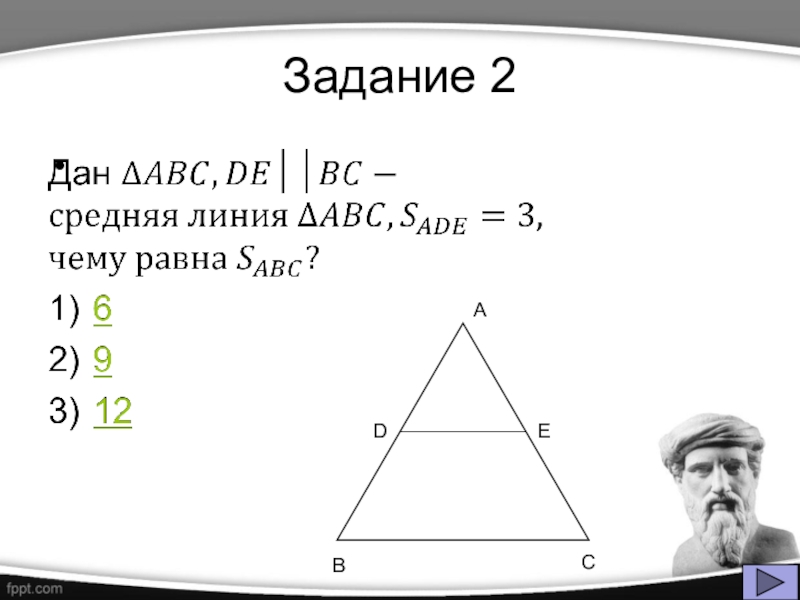
- 24. Задание 2
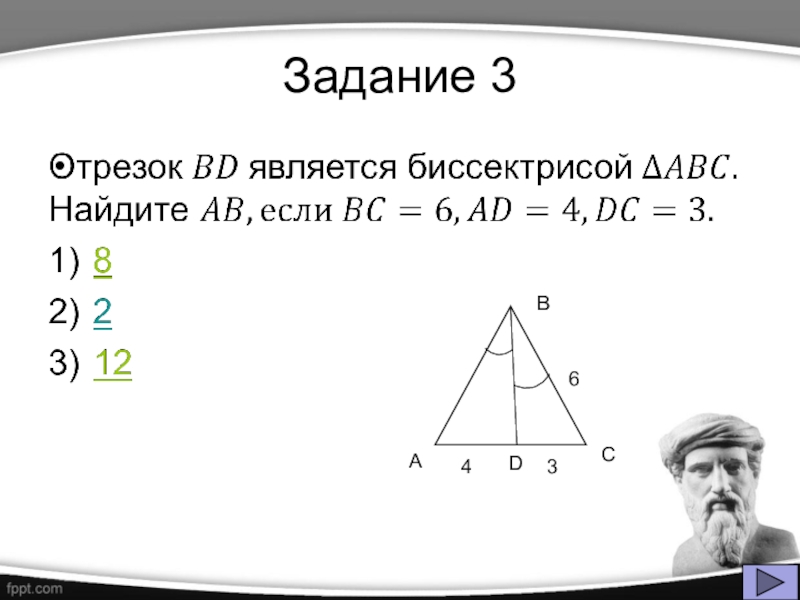
- 25. Задание 3
- 26. Задание 4
- 27. Задание 5
- 28. ТЕСТОКОНЧЕН
- 29. ВЕРНО!
- 30. О ш и б к а !
Историческая справкаСвойства элементов треугольникаПримеры решения задачТест Опорные задачи
Слайд 3Историческая справка
Треугольник-это простейшая фигура: три стороны и три вершины. Математики его
называют двумерным симплексом. «Симплекс» по-латыни означает простейший. Трёхмерным симплексом называют треугольную пирамиду. Именно в силу своей простоты треугольник явился основной многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звёзд используют свойства треугольников. Так возникла наука тригонометрия – наука об измерении треугольников, о выражении сторон через углы.
Слайд 4 Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник
на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу. В одном египетском папирусе 4000-летней давности говорится, что площадь равнобедренного треугольника равна произведению половины основания на боковую сторону (а не на высоту).
Через 2000 лет в Древней Греции изучение свойств треугольника ведётся очень активно. Пифагор открывает свою теорему. Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны; становится известным, что биссектрисы, как медианы и высоты, пересекаются в одной точке.
Через 2000 лет в Древней Греции изучение свойств треугольника ведётся очень активно. Пифагор открывает свою теорему. Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны; становится известным, что биссектрисы, как медианы и высоты, пересекаются в одной точке.
Слайд 5
Термин «медиана» происходит от латинского слова mediana – «средняя» (линия); «перпендикуляр»
- от латинского слова perpendicularis – «отвесный». Термин был образован в средние века. «Биссектриса» - от латинских слов bis (дважды, надвое) и sectrix (секущая).
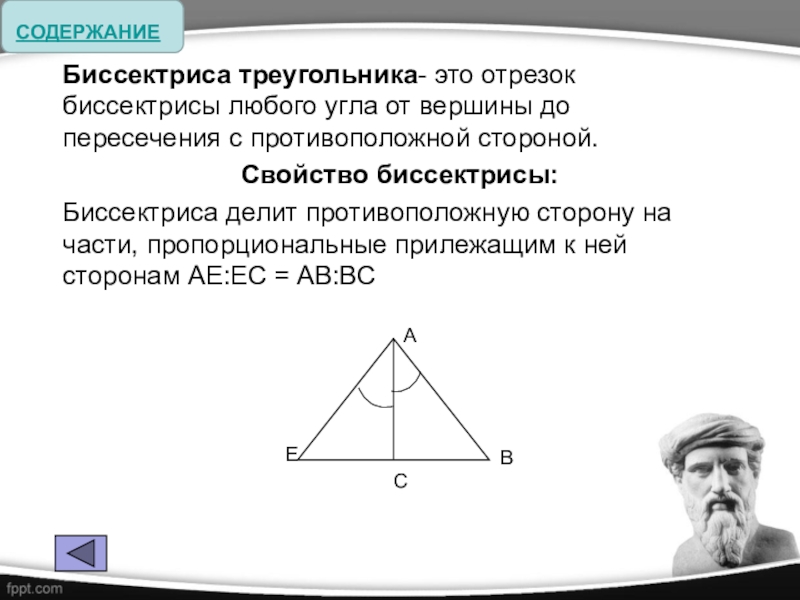
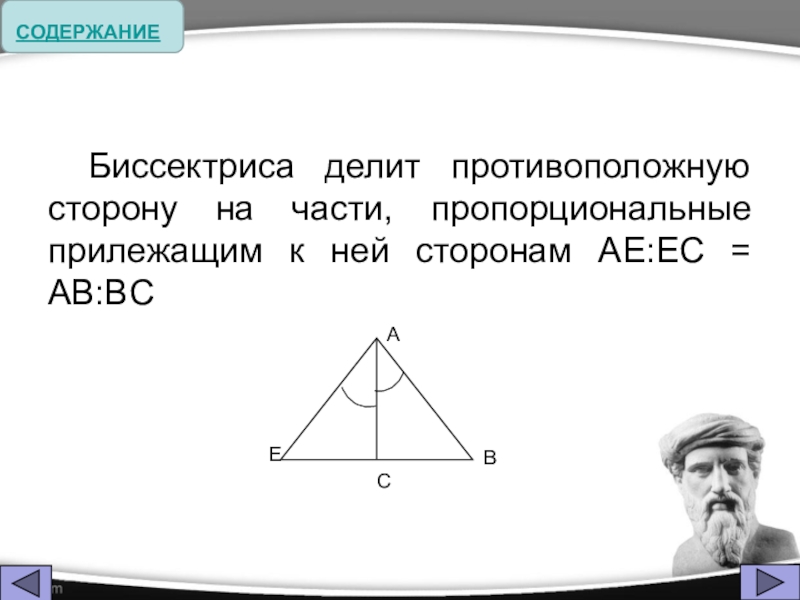
Слайд 8Биссектриса треугольника- это отрезок биссектрисы любого угла от вершины до пересечения
с противоположной стороной.
Свойство биссектрисы:
Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам AE:EC = AB:BC
Свойство биссектрисы:
Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам AE:EC = AB:BC
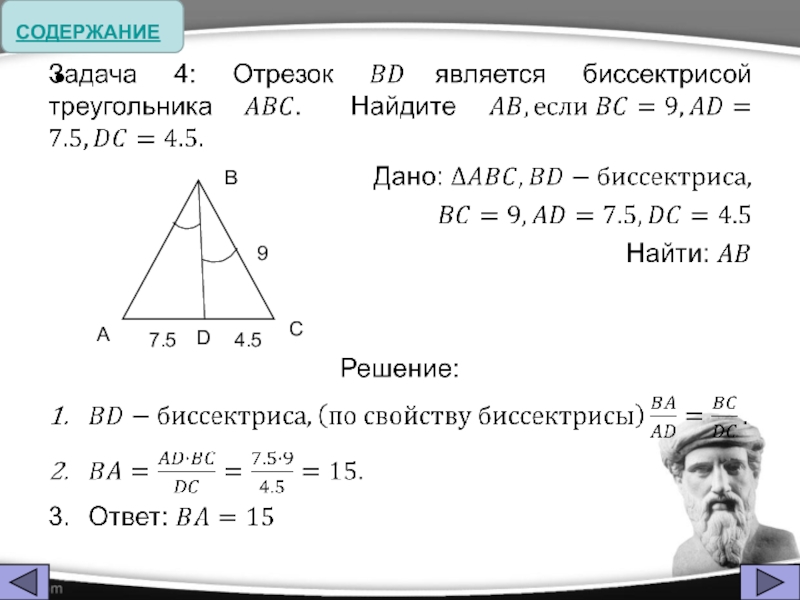
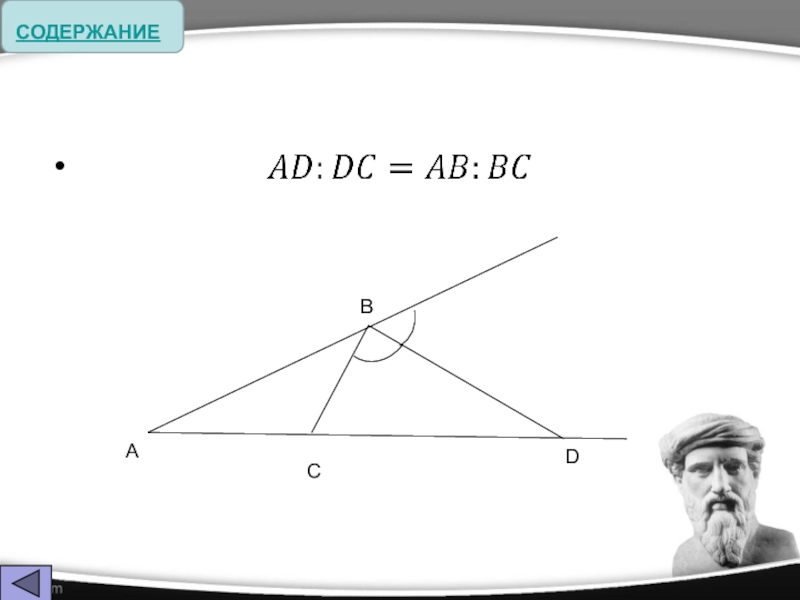
Слайд 21 Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам
AE:EC = AB:BC