- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему : Задачи на смеси и сплавы. Метод Магницкого.
Содержание
- 1. : Задачи на смеси и сплавы. Метод Магницкого.
- 2. Решение текстовых задач представляет трудность для многих
- 3. Задачи на смеси и сплавы вызывают наибольшее
- 4. Задачам подобного типа уделялось значительное внимание в
- 5. Пусть q – массовая доля вещества в
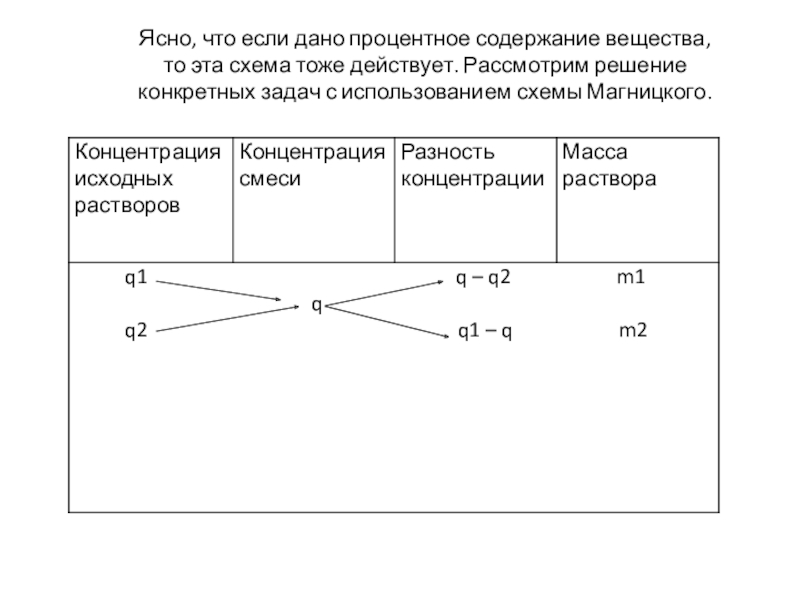
- 6. Ясно, что если дано процентное содержание вещества,
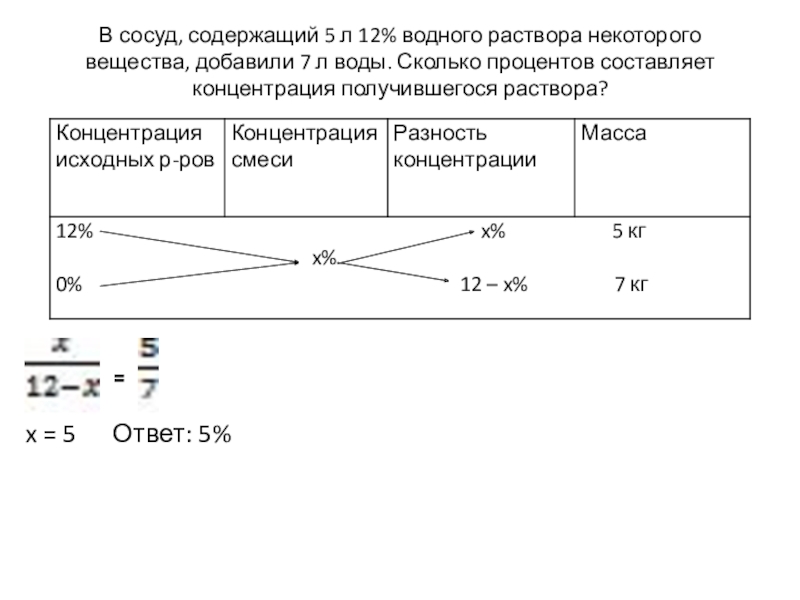
- 7. В сосуд, содержащий 5 л 12% водного
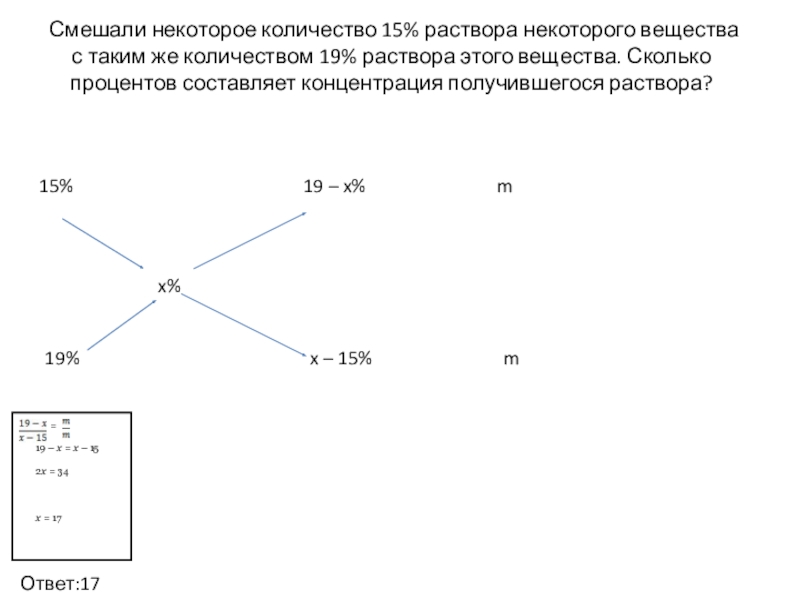
- 8. Смешали некоторое количество 15% раствора некоторого
- 9. Имеется 2 сплава. Первый содержит 10%
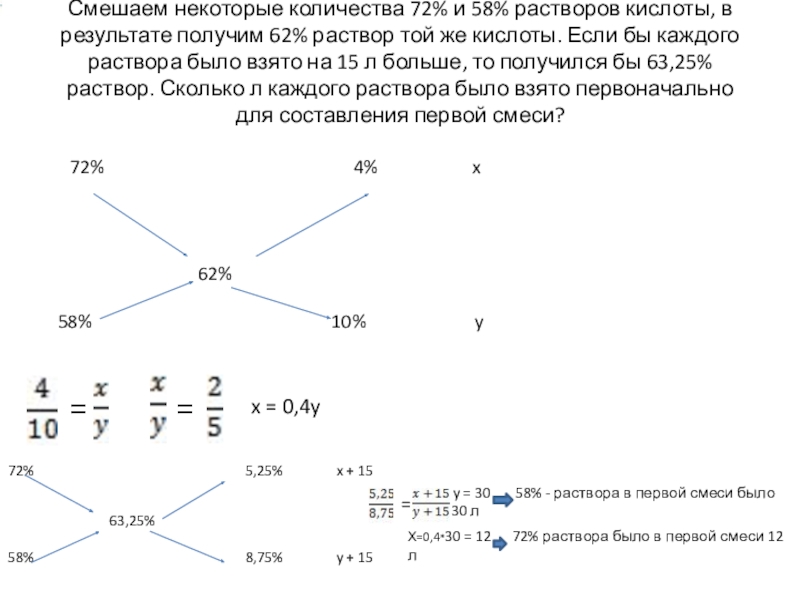
- 10. Смешаем некоторые количества 72% и 58% растворов
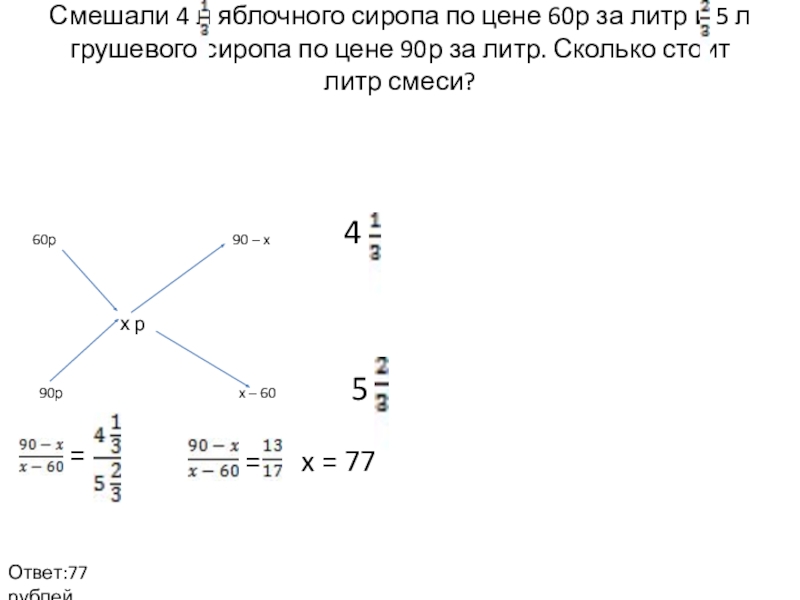
- 11. Смешали 4 л яблочного сиропа по цене
- 12. Подведем итог: способ Магницкого дает возможность структурировать
- 13. Спасибо за внимание
Слайд 2Решение текстовых задач представляет трудность для многих учеников. Одна из причин:
Слайд 3Задачи на смеси и сплавы вызывают наибольшее затруднение у ребят, а
Слайд 4Задачам подобного типа уделялось значительное внимание в «Арифметике» Леонтия Филипповича Магницкого.
Слайд 5Пусть q – массовая доля вещества в растворе, m – масса
Слайд 6Ясно, что если дано процентное содержание вещества, то эта схема тоже
Слайд 7В сосуд, содержащий 5 л 12% водного раствора некоторого вещества, добавили
=
x = 5 Ответ: 5%
Слайд 8 Смешали некоторое количество 15% раствора некоторого вещества с таким же
=
19 – x = x – 15
2x = 34
x = 17
15% 19 – x% m
x%
19% x – 15% m
Ответ:17%
Слайд 9 Имеется 2 сплава. Первый содержит 10% никеля, второй - 30%
10% 5% x
25%
30% 15% 200 - x
; x=50; 2)200 – 50 = 150 - 2 сплав; 3) 150 – 50 = 100 – разница;
Ответ: 100 кг
Слайд 10Смешаем некоторые количества 72% и 58% растворов кислоты, в результате получим
72% 4% x
62%
58% 10% y
=
=
x = 0,4y
72% 5,25% x + 15
63,25%
58% 8,75% y + 15
=
y = 30 58% - раствора в первой смеси было 30 л
Х=0,4*30 = 12 72% раствора было в первой смеси 12 л
Слайд 11Смешали 4 л яблочного сиропа по цене 60р за литр и
60р 90 – x
х р
90р x – 60
4
5
=
=
x = 77
Ответ:77 рублей