Презентация, доклад на тему Разбор задач демоверсий ЕГЭ_Строки_Цепочки

из одного символа – латинской буквы «А». Каждая из последующих цепочек создается такими действиями: в очередную строку сначала записывается буква, чей порядковый номер в алфавите соответствует номеру строки (на i-м шаге пишется «i»-я буква алфавита), к ней справа дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу: (1) A (2) BAA (3) CBAABAA (4) DCBAABAACBAABAA Латинский алфавит (для справки): ABCDEFGHIJKLMNOPQRSTUVWXYZ
Запишите семь символов подряд, стоящие в восьмой строке со 126-го по 132-е место (считая слева направо).

Разбор задачи B8

E1515                                      63
(7) G F E1515 E1515 F E1515 E1515       126
(8) H G F E1515 E1515 F E1515 E1515 G F E1515 E1515 F E1515 E1515            
                4     34       65                   128   
126  127  128   G    F    E   132
                        B     A      A   G    F    E    D    
     Ответ: BAAGFЕD                                                                                        

Решение (1-й способ)

шаг
(5) E()()                                           
(6) F E()() E()()
(7) G FE()()E()() FE()()E()()
(8) H GFE()()E()()FE()()E()() GFE()()E()()FE()()E()()
Чтобы определить позиции символов, нужно определить, сколько символов образуется на каждом шаге.
Количество символов определяется по формуле:
  Ni=2i-1, где i - шаг                       
На 7-м шаге образуется N7=27-1=127 символов:
(7) G FE()()E()() FE()()E()()127

Решение (2-й способ)

элемент находится в позиции:
1+N7=128:
(8) H1 GFE()()E()()FE()()E()()128 GFE()()E()()FE()()E()()
Нам нужно найти позиции от 126-и до 132-х
Расставим позиции:
(8) H1 GFE()()E()()FE()()E()()128 G129F130E131()()E()()FE()()E()()
Элементы в позициях 126, 127,128, 132 нужно смотреть в ()
D132CBAABAACBAAB126A127A128
Ответ: BAAGFED 
                                                                                        

Решение (2-й способ, продолжение)

из одного символа – латинской буквы «А». Каждая из последующих цепочек создается такими действиями: в очередную строку сначала записывается буква, чей порядковый номер в алфавите соответствует номеру строки (на i-м шаге пишется i-я буква алфавита), к ней слева дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(1) A (2) AAB (3) AABAABC (4) AABAABCAABAABCD Латинский алфавит (для справки): ABCDEFGHIJKLMNOPQRSTUVWXYZ
Имеется задание:
«Определить символ, стоящий в n-й строке на позиции 2n–1– 5, считая от левого края цепочки».
Выполните это задание для n = 8.

Разбор задачи B8

с 5-го по 8-й шаг
(5) E()()                                           
6)()()E ()()E F
(7) ()()E()()EF ()()E()()EF G
(8) ()()E()()EF()()E()()EFG ()()E()()EF()()E()()EFG H
Чтобы определить позиции символов, нужно определить, сколько символов образуется на каждом шаге.
Количество символов определяется по формуле:
  Ni=2i-1, где i - шаг                       
На 7-м шаге образуется N7=27-1=127 символов:
(7) ()()E()()EF ()()E()()EF G127

Решение (2-й способ)

позицию
До 127 позиции символов на 7-м и 8-м шаге одинаковы:
(7) ()()E()()EF ()()E()()EF G
(8) ()()E()()EF()()E()()EFG ()()E()()EF()()E()()EFG H
Поэтому будем смотреть по 7-му шагу.
Так проще, т.к. там меньше элементов.
Определим позиции элементов, близкие к искомому
(7) ()()E()()EF ()()E()()E125F126 G127
Получается, что элемент в позиции 123 нужно смотреть в ():
(4) AABAABCAABAABC123D124
Ответ: С 
                                                                                        

Решение (2-й способ, продолжение)

цепочки стоит одна из бусин A, B, Г. На втором – одна из бусин А, Б, В. На первом месте - одна из бусин A, B, Г, не стоящая в цепочке на втором или третьем месте. Какая из перечисленных цепочек могла быть создана с учетом этих правилу?
БГВ 2) ГБА 3) БАВ 4) ГВГ
Решение:
Рассмотрим все предложенные варианты:






Ответ: 2

Разбор задачи А11 (демо 2008), А12 (демо 2009)

виде 30. Укажите это основание.
Решение:
Обозначим основание искомой системы счисления как x
18=х*3+0. Отсюда,
х=18/3=6.
Ответ: 6

Определение оснований систем счисления.
Разбор задачи B5 (демо ЕГЭ 2011)

виде 100. Укажите это основание.
Решение:
Обозначим основание искомой системы счисления как x
49=x2*1+0+0=x2=>x=±7.
Основание системы счисления не может быть отрицательным, поэтому оно равно 7.
Ответ: 7

Разбор задачи B3 (демо ЕГЭ 2010)

в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Решение:
При переводе числа из десятичной системы в другую, мы делим десятичное число на основание другой системы счисления. 
Первый остаток от деления - это последняя цифра числа в этой системе счисления. Чтобы в остатке был 0, мы должны подобрать десятичное число, которое будет кратно основанию системы счисления, в которую переводим.
Для системы с основанием 3, такими числами могут быть: 3, 6, 9 и т.д. Для системы с основанием 5 - 5, 10, 15 и т.д. 
По заданию, число должно быть минимально, поэтому для системы с основанием 3 - это число 3, а с основанием 5 - это число 5.
3|3        5|5 3 1        5  1 0           0
310=103 и 510=103

Разбор задачи B7 (демо ЕГЭ 2013)

остатком 3 и 5), десятичное число должно быть кратно числам: 3 и 5. 
Решение:
3*5=15 - это и есть искомое десятичное число.
15|3         15|5 15 5         15  3   0              0
1510=503 и 1510=305
Ответ: 15

Разбор задачи B7 (демо ЕГЭ 2013, продолжение)

8?
Решение:
Приведем к единому основанию: 
22*2014 + 22015 – 23
24028 + 22015 – 23
Рассмотрим 1-ым действием вычитание:




При сложении замечаем, что в 1-м слагаемом только одна единица, и она расположена левее единиц 2-го слагаемого.
Следовательно, при сложении получим число 2012+1

Ответ: 2013

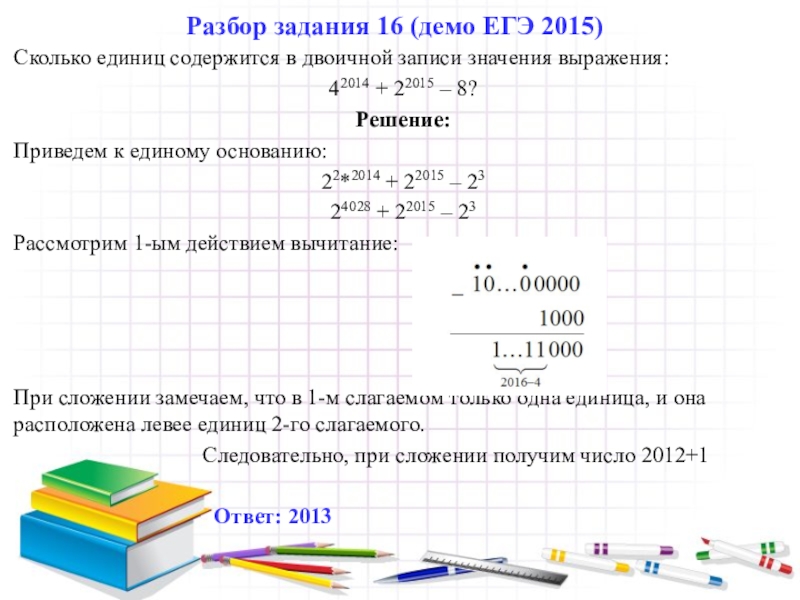
Разбор задания 16 (демо ЕГЭ 2015)

→ 1000
Выполним вычитание: ● ● ● ● ● ●
1000000000
1000

111111000

Ответ: 6

Разбор задания 16