Презентация, доклад по теме Разбор заданий из ЕГЭ

одной или нескольким более простым задачам того же типа
Чтобы определить рекурсию, нужно задать
условие остановки рекурсии (базовый случай или несколько базовых случаев)
рекуррентную формулу
Любую рекурсивную процедуру можно запрограммировать с помощью цикла
Рекурсия позволяет заменить цикл и в некоторых сложных задачах делает решение более понятным, хотя часто менее эффективным

forward;
procedure G(n: integer); forward;
procedure F(n: integer);
begin
if n > 0 then
G(n - 1);
end;
procedure G(n: integer);
begin
writeln('*');
if n > 1 then
F(n - 2);
end;
Сколько символов «звёздочка» будет напечатано на экране при выполнении
вызова F(11)?

Forward (процедурная директива)
Используя Forward-описания (предописания), можно делать процедуры или функции известными без фактического определения их операторной части.
С точки предописания, другие процедуры и функции могут вызывать предописанную подпрограмму, делая возможной взаимную рекурсию.

Решение:
1) Цепочка вызовов: F(11) → G(10) → F(8) → G(7) → F(5) → G(4) → F(2) → G(1)
2) За один вызов функции G выводится одна звёздочка, внутри функции F звездочки не выводятся
Ответ: 4

then begin
F(n + 1);
F(n + 3)
end
end;
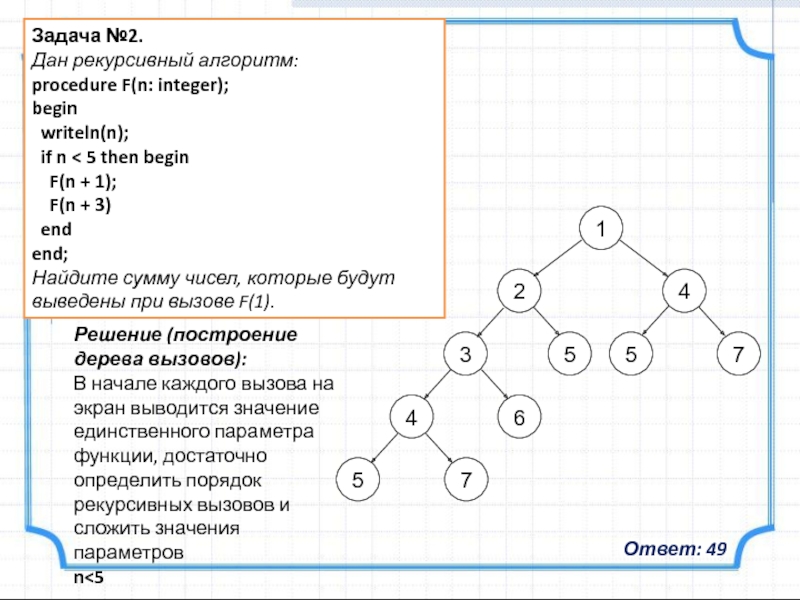
Найдите сумму чисел, которые будут выведены при вызове F(1).

Решение (построение дерева вызовов):
В начале каждого вызова на экран выводится значение единственного параметра функции, достаточно определить порядок рекурсивных вызовов и сложить значения параметров
n<5

Ответ: 49

then begin
F(n+2);
F(n*3)
end
end;
Найдите сумму чисел, которые будут выведены при вызове F(1).

Решение (динамическое программирование)
1) Определим рекуррентную формулу;
G(n) сумма чисел, которая выводится при вызове F(n)
2) n >= 6: процедура выводит число n:
G(n) = n при n >= 6
3) n < 6: процедура выводит число n и дважды вызывает сама себя:
G(n) = n + G(n+2) + G(3n) при n < 6

6

7

8

9

10

11

12

13

14

15

27

22

39

30

79

Ответ: 79

then begin
F(n-2);
F(n div 2)
end
end;
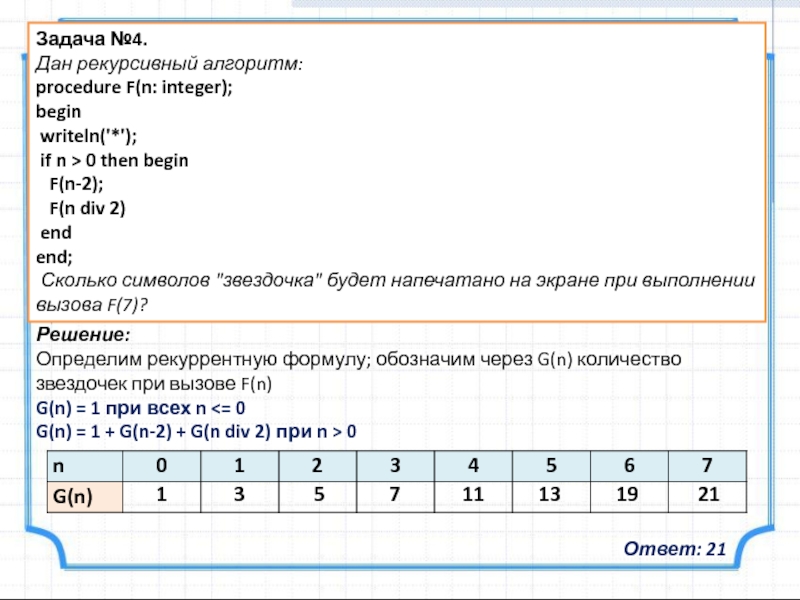
Сколько символов "звездочка" будет напечатано на экране при выполнении вызова F(7)?

Решение:
Определим рекуррентную формулу; обозначим через G(n) количество звездочек при вызове F(n)
G(n) = 1 при всех n <= 0
G(n) = 1 + G(n-2) + G(n div 2) при n > 0

1

3

5

7

11

13

19

21

Ответ: 21

– натуральное число, задан следующими соотношениями:
F(1) = 1; G(1) = 1;
F(n) = F(n – 1) – G(n – 1),
G(n) = F(n–1) + G(n – 1), при n >=2
Чему равно значение величины F(5)/G(5)? В ответе запишите только целое число.

Решение:

Ответ: 1

число,
задан следующими соотношениями:
F(1) = 1
F(n) = F(n–1) * n, при n > 1
Чему равно значение функции F(5)?
В ответе запишите только целое число.

Решение:
F(5) = F(4) * 5
F(5) = F(3) * 4 * 5
F(5) = F(2) * 3 * 4 * 5
F(5) = F(1) * 2 * 3 * 4 * 5
F(5) = 1 * 2 * 3 * 4 * 5

Ответ: 120

образом (язык Паскаль):
procedure F(n: integer);
begin
if n < 3 then
write('*')
else begin
F(n-1);
F(n-2);
F(n-2)
end;
end;
Сколько звездочек напечатает эта процедура при вызове F(6)? В ответе запишите только целое число.

Решение:
Для n < 3 (то есть, для 1 и 2) функция выводит одну звездочку
F(1) = F(2) = 1
Для n>=3 рекуррентная формула
F(n) = F(n-1) + F(n-2) + F(n-2)
= F(n-1) + 2*F(n-2)

1

1

3

5

11

21

Ответ: 21

значение–результат
функция располагается выше основной программы:
function F(x: integer):integer;
begin
...
F:= <результат функции>
end;
результат функции записывается в специальную переменную, имя которой совпадает с именем функции; объявлять эту переменную не нужно

Если квадратный трехчлен задан в виде


, то абсцисса, соответствующая точке минимума, вычисляется по формуле

k, при которых приведённая ниже программа выводит тот же ответ, что и при входном значении k = 10. Значение k = 10 также включается в подсчёт различных значений k.
var k, i : longint;
function f(n: longint) : longint;
begin
f := n * n * n;
end;
begin
readln(k);
i := 1;
while f(i) < k do
i:= i+1;
if f(i)-k <= k-f(i-1) then
writeln(i)
else writeln(i-1);
end.

Решение:
Функция f возвращает куб переданного ей числа
После ввода k работает цикл, который увеличивает i до тех пор, пока значение куба f(i) не станет больше или равно k
построим таблицу значений функции f(i) (кубов чисел):

При k=10 цикл завершится при i=3
При k=10 и i=3 условие
f(i)-k <= k-f(i-1)
27-10 <= 10-8
17 <= 2
⇒ выводится на экран не i, а i-1, то есть 2
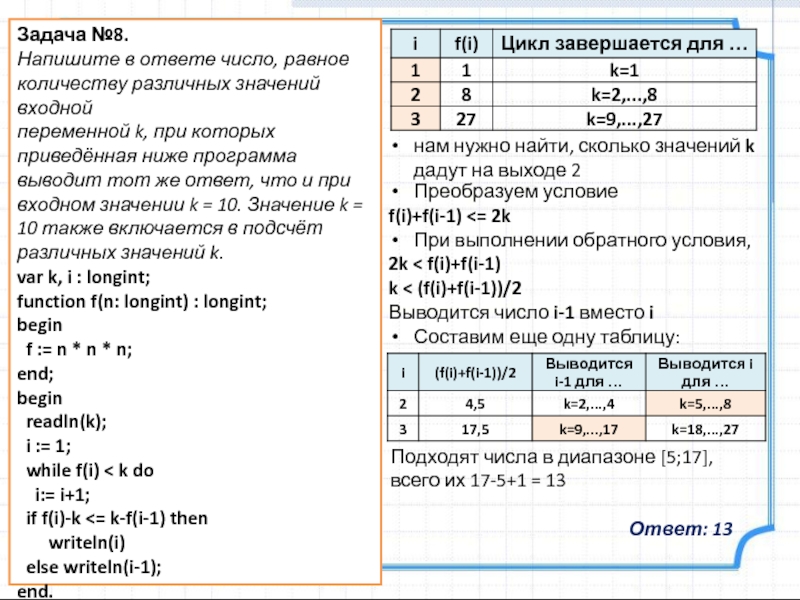
итак, нам нужно найти, сколько значений k дадут на выходе 2

k, при которых приведённая ниже программа выводит тот же ответ, что и при входном значении k = 10. Значение k = 10 также включается в подсчёт различных значений k.
var k, i : longint;
function f(n: longint) : longint;
begin
f := n * n * n;
end;
begin
readln(k);
i := 1;
while f(i) < k do
i:= i+1;
if f(i)-k <= k-f(i-1) then
writeln(i)
else writeln(i-1);
end.

нам нужно найти, сколько значений k дадут на выходе 2

Преобразуем условие
f(i)+f(i-1) <= 2k
При выполнении обратного условия,
2k < f(i)+f(i-1)
k < (f(i)+f(i-1))/2
Выводится число i-1 вместо i
Составим еще одну таблицу:

Подходят числа в диапазоне [5;17], всего их 17-5+1 = 13

Ответ: 13

в результате выполнения следующего алгоритма, было наименьшим.
var a,b,t,M,R,H :integer;
Function F(H, x: integer):integer;
begin
F := 11*(x-H)*(x-H)+13;
end;
BEGIN
readln(H);
a := -10; b := 30;
M := a; R := F(H, a);
for t := a to b do begin
if (F(H, t) > R) then begin
M := t;
R := F(H, t)
end
end;
write(R)
END.

Решение:
В результате анализа можно сделать вывод, что цикл ищет максимум функции F(H,t) на интервале от a до b
Выводится значение R, а величина M не выводится и не влияет на вычисление R
Функция F вычисляет значение
F:=11*(x-H)*(x-H) + 13;
график этой эта функции – парабола с ветвями, направленными вверх

Вершина параболы находится в точке x = H При изменении H парабола двигается влево или вправо (но не вверх-вниз!)
Итак, мы ищем максимальное значение квадратичной функции, и хотим, чтобы это значение было наименьшим

середине отрезка [a; b]
⇒ H равно среднему арифметическому между a = –10 и b = 30:
H = (–10 + 30) / 2 = 10
Ответ: 10

при которых программа выдаёт тот же ответ, что и при входном значении k = 35. Значение k = 35 также включается в подсчёт различных значений k.
var k, i : longint;
function F(x: longint) : longint;
begin
F:=2*x*x+3*x+2
end;
begin
i := 15;
readln(K);
while (i> 0) and (F(i) > K) do
i:=i-1;
writeln(i)
end.

Решение:
Вычислим значения функции F при i=1,2,3…
i=0: f(0)=2
i=1: f(1)=7
i=2: f(2)=16
i=3: f(3)=29
i=4: f(4)=46
К ∈ [29;45]
⇒ 45-29+1=17 чисел
Ответ: 17