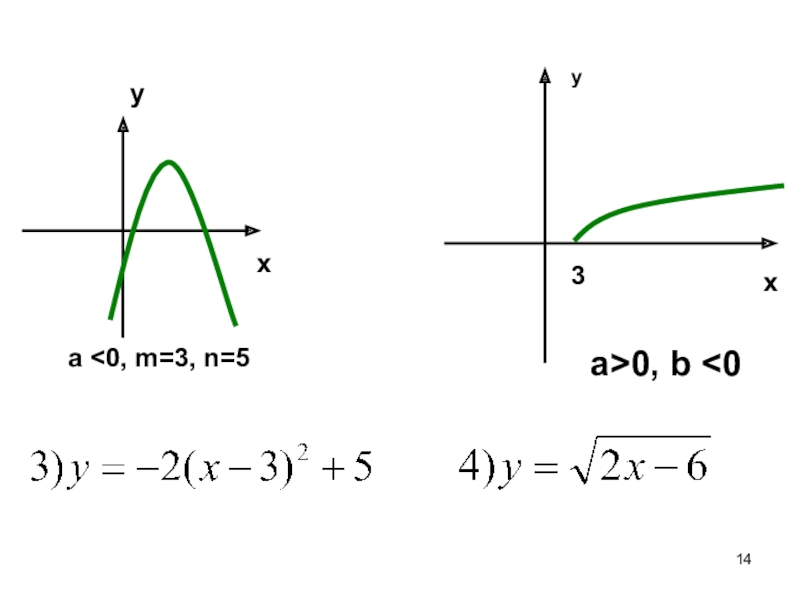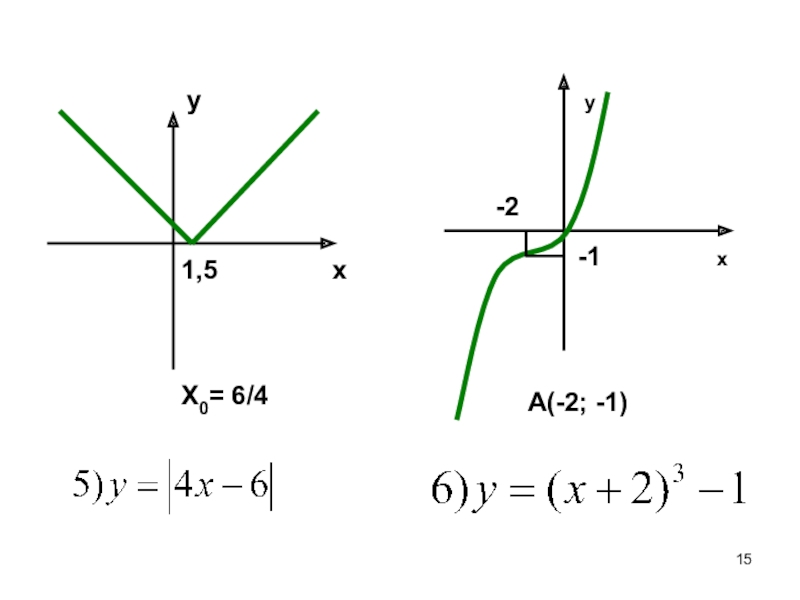- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Нахождение корней систем уравнений и уравнений с помощью графиков.
Содержание
- 1. Презентация по теме Нахождение корней систем уравнений и уравнений с помощью графиков.
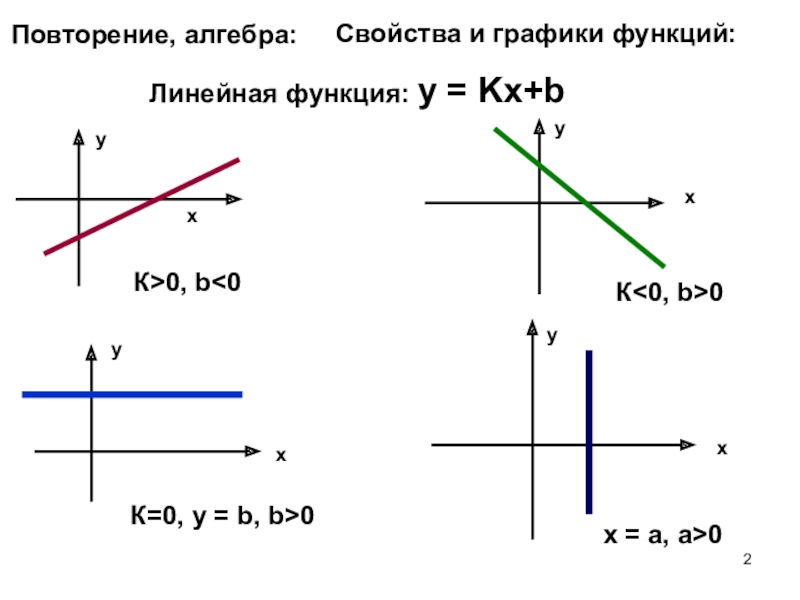
- 2. Повторение, алгебра:Свойства и графики функций:Линейная функция: у = Kх+bххууК>0, b0x = a, a>0
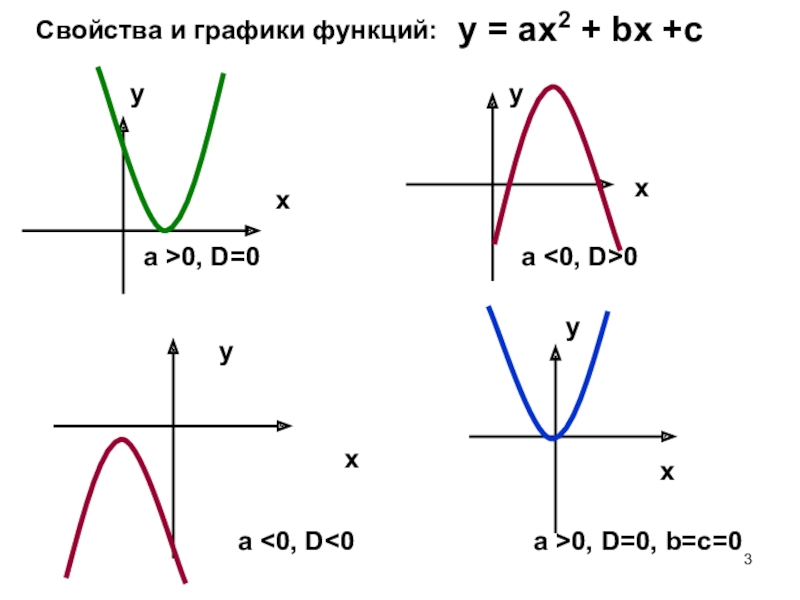
- 3. Свойства и графики функций:у = ах2 + bх +сa >0, D=0a 0xxxxyyyya >0, D=0, b=c=0a
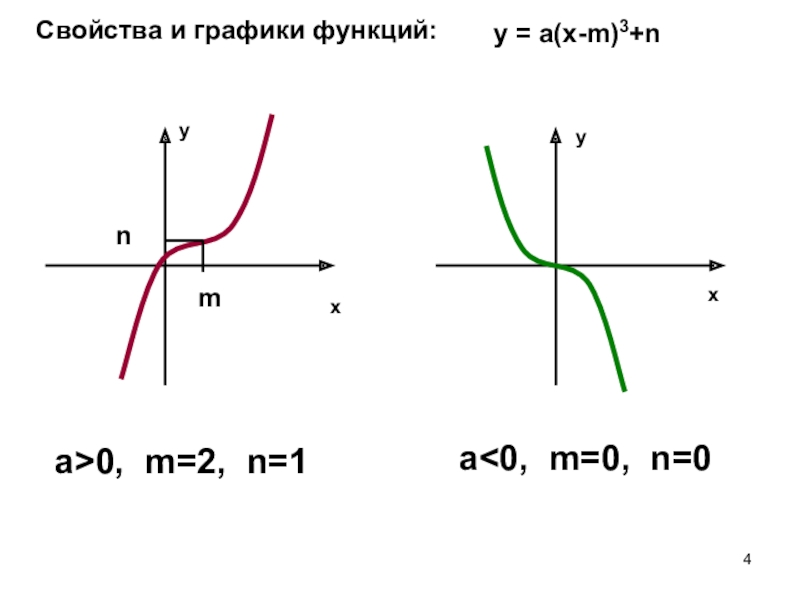
- 4. Свойства и графики функций:y = а(х-m)3+na>0, m=2, n=1a
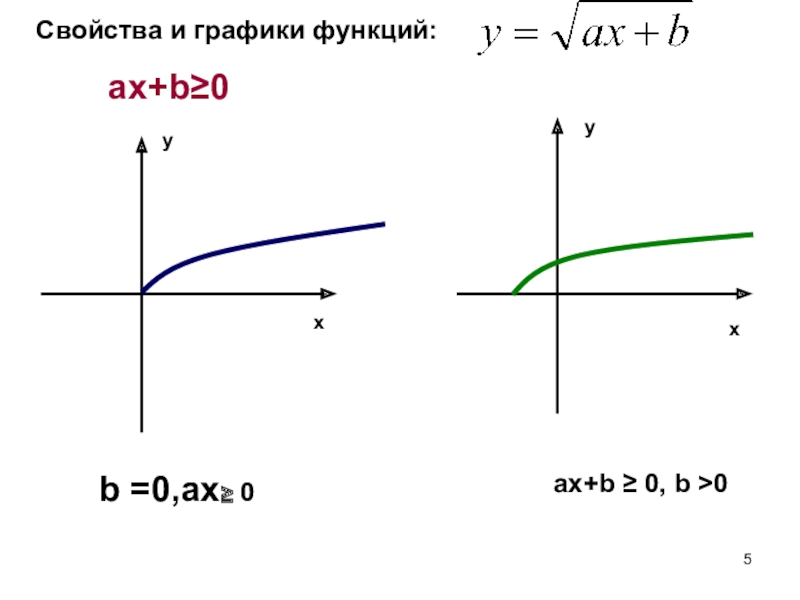
- 5. Свойства и графики функций:ax+b≥0xxyyb =0,ax≥ 0 ax+b ≥ 0, b >0
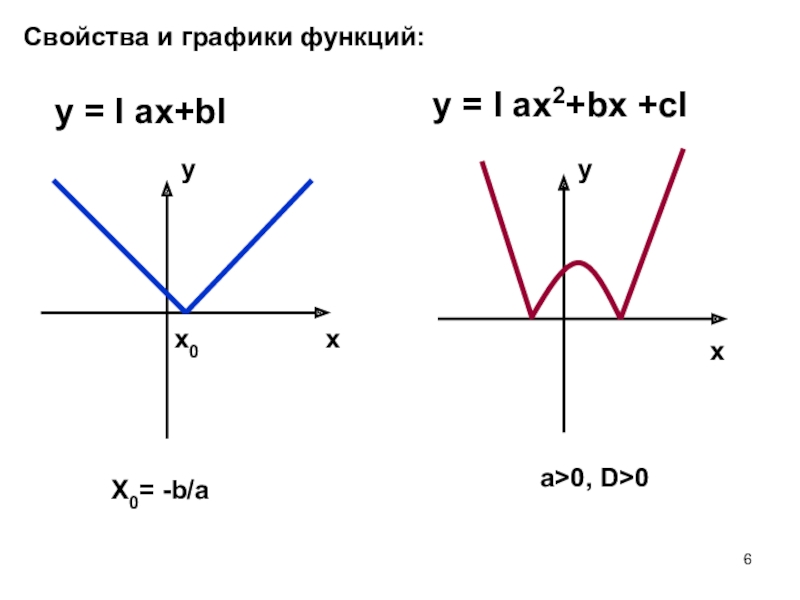
- 6. Свойства и графики функций:y = I ax+bIy = I ax2+bx +cIx0a>0, D>0X0= -b/axxyy
- 7. ххуу(х – а)2 + (х – b)2
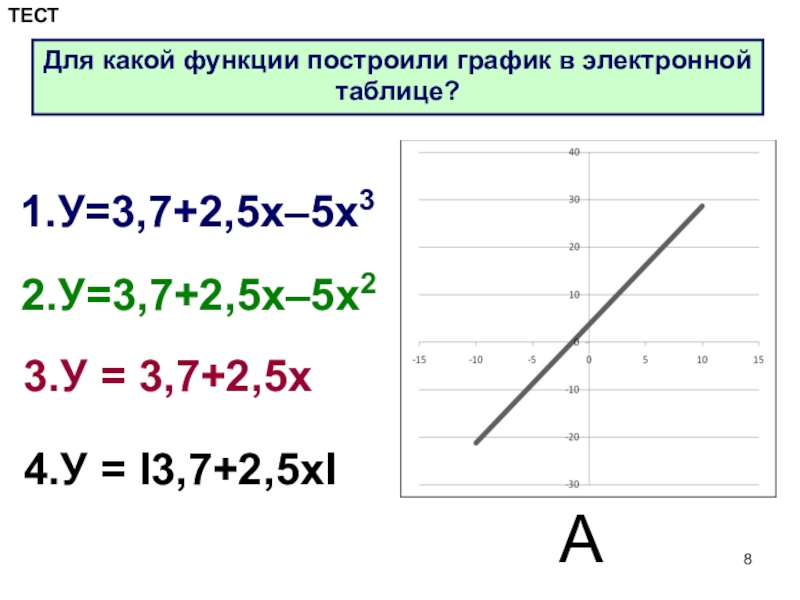
- 8. 1.У=3,7+2,5х–5х32.У=3,7+2,5х–5х23.У = 3,7+2,5х4.У = I3,7+2,5хIАДля какой функции построили график в электронной таблице?ТЕСТ
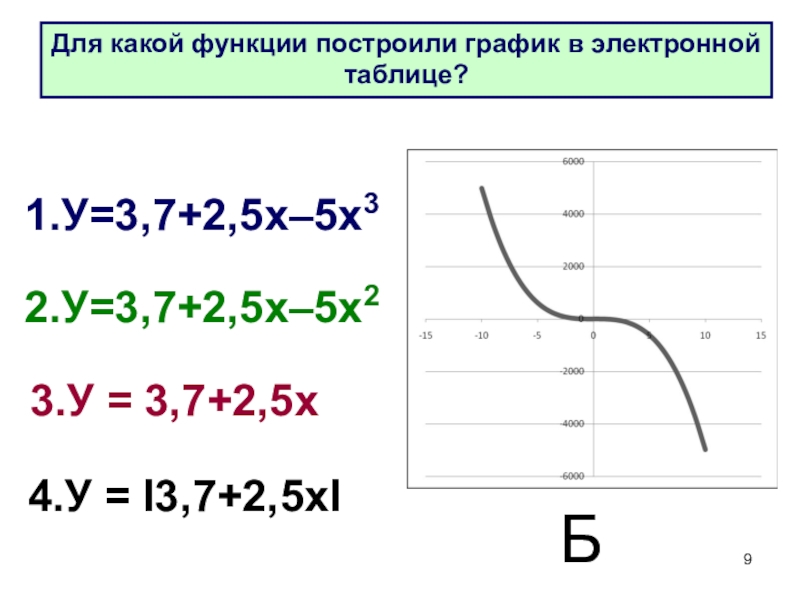
- 9. 1.У=3,7+2,5х–5х32.У=3,7+2,5х–5х23.У = 3,7+2,5х4.У = I3,7+2,5хIБДля какой функции построили график в электронной таблице?
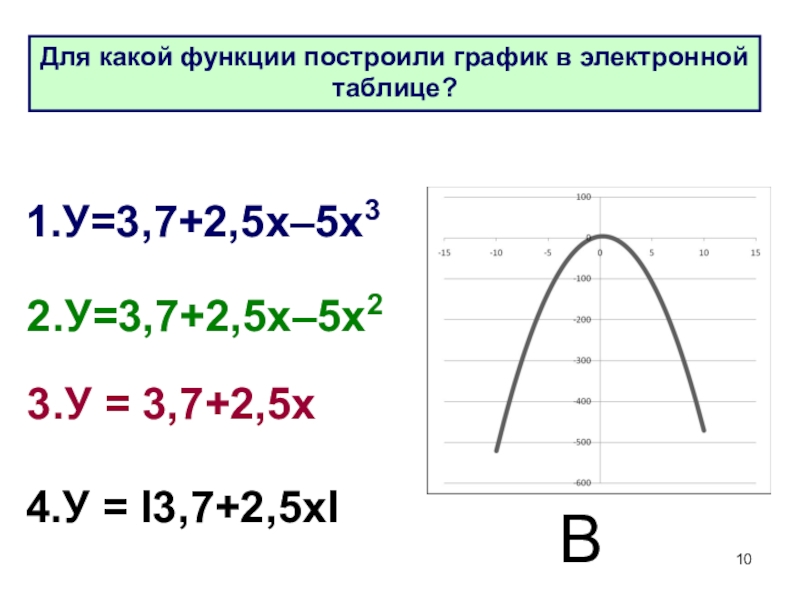
- 10. 1.У=3,7+2,5х–5х32.У=3,7+2,5х–5х23.У = 3,7+2,5х4.У = I3,7+2,5хIВДля какой функции построили график в электронной таблице?
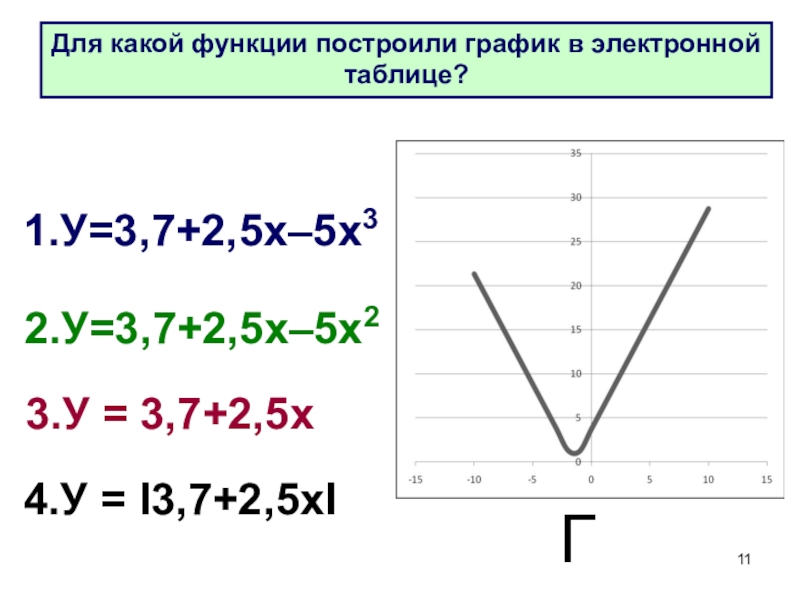
- 11. 4.У = I3,7+2,5хI1.У=3,7+2,5х–5х32.У=3,7+2,5х–5х23.У = 3,7+2,5хГДля какой функции построили график в электронной таблице?
- 12. 2) у = х2 - 4х -
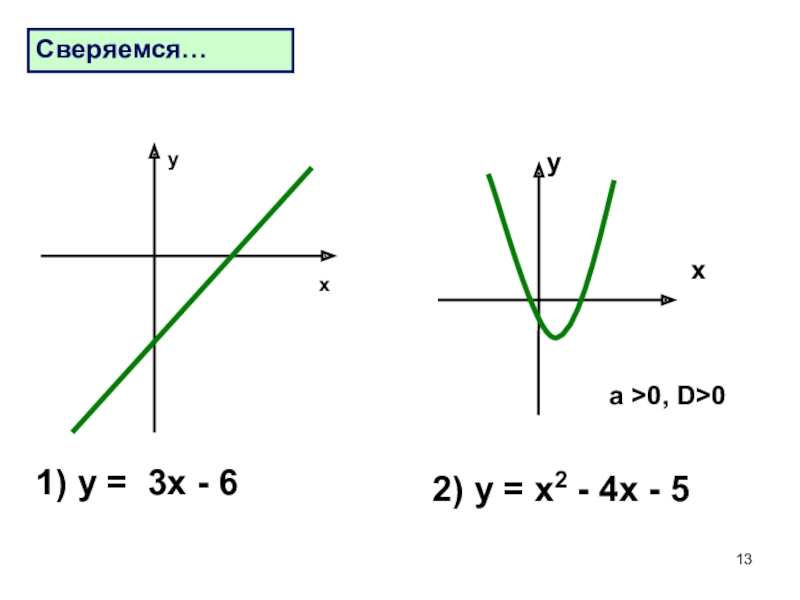
- 13. 1) у = 3х - 6Сверяемся…ху2) у = х2 - 4х - 5a >0, D>0xy
- 14. a 0, b
- 15. 1,5X0= 6/4xyxyA(-2; -1)-2-1
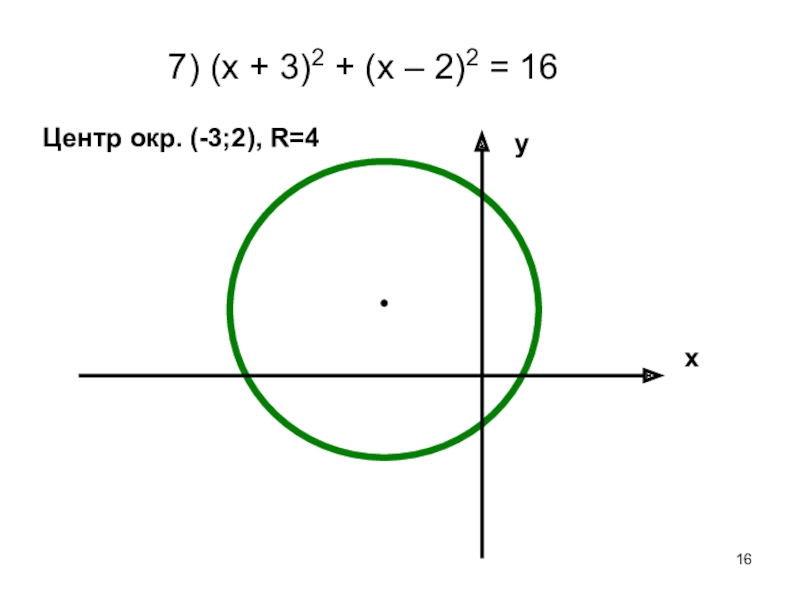
- 16. 7) (х + 3)2 + (х – 2)2 = 16хуЦентр окр. (-3;2), R=4
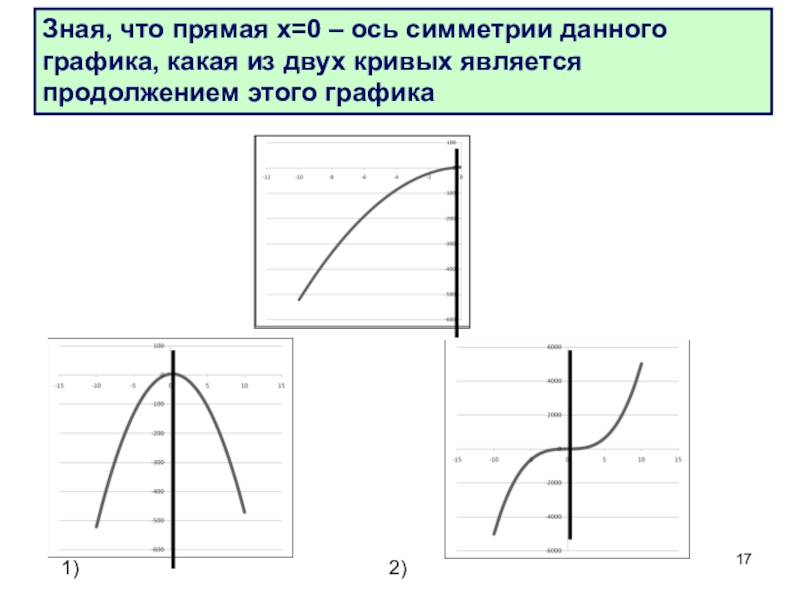
- 17. Зная, что прямая х=0 – ось симметрии
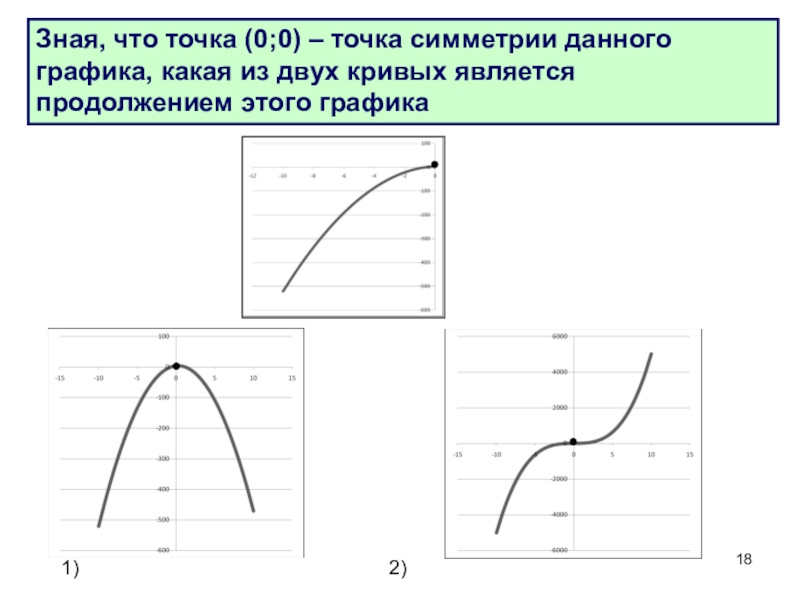
- 18. Зная, что точка (0;0) – точка симметрии
- 19. ТЕСТКакие формулы, написанные при построении графиков в
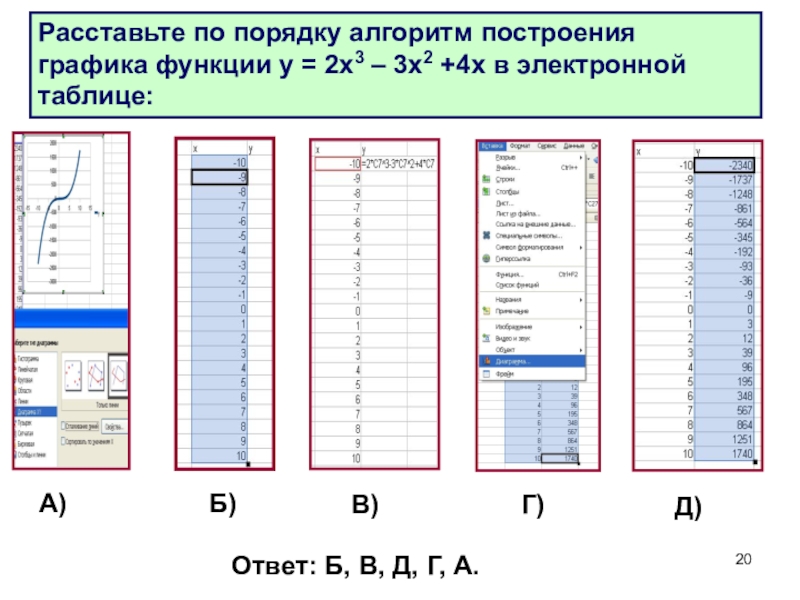
- 20. Расставьте по порядку алгоритм построения графика функции
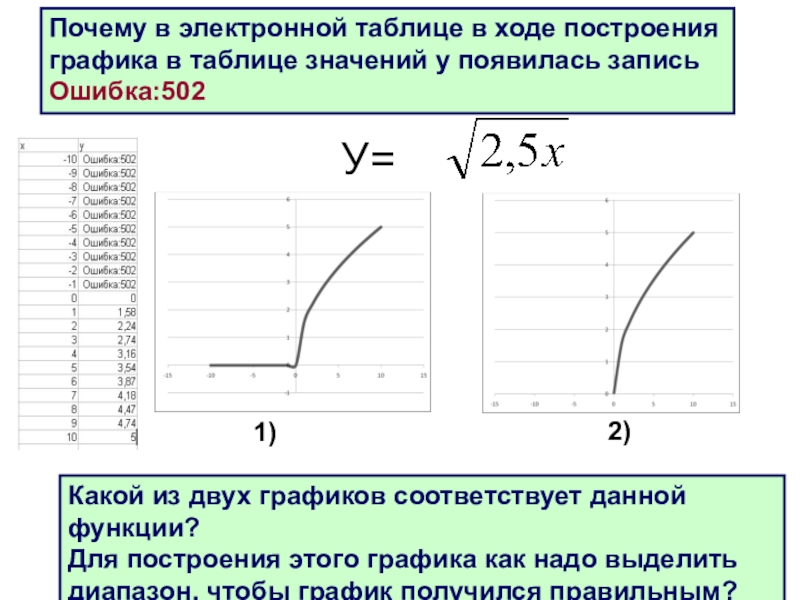
- 21. У= Почему в электронной таблице в ходе
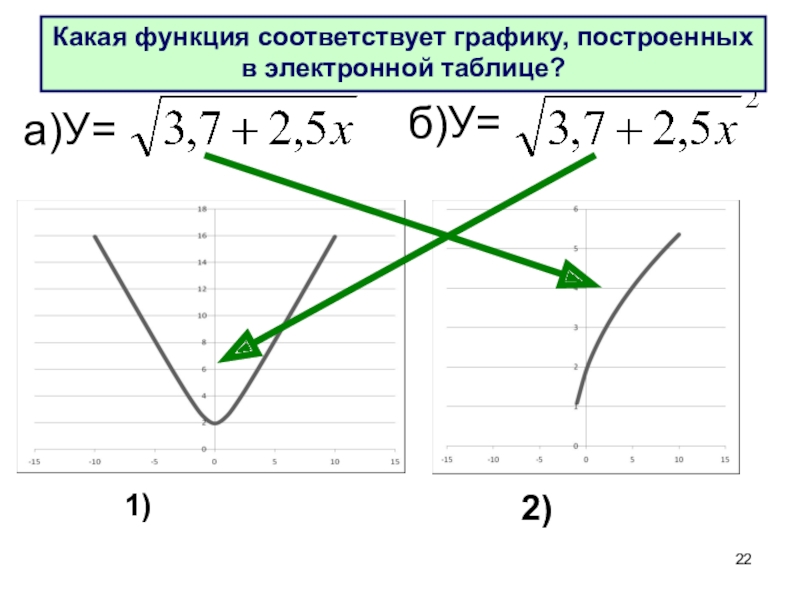
- 22. а)У= б)У= Какая функция соответствует графику, построенных в электронной таблице?2)1)
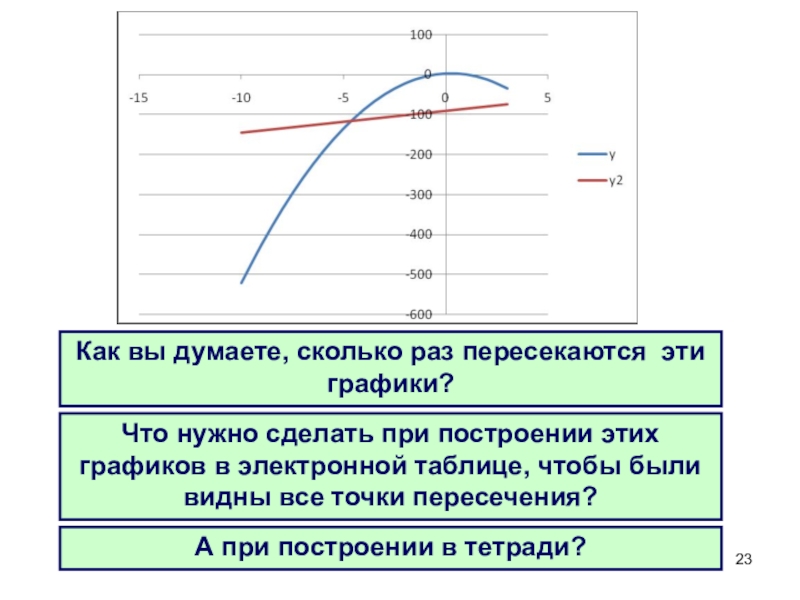
- 23. Как вы думаете, сколько раз пересекаются эти
- 24. Функция задана формулой: Нужно построить график этой
- 25. Сколько общих точек имеют графики функций?Как можно с помощью графиков узнать сколько решений имеет система уравнений?xxyy
- 26. Объяснение материала: Решаются задачи в электронной таблице:у=4х2-3х+5у=х-2х2+15Ответ:
- 27. 2) Как узнать с помощью графиков сколько решений имеет система уравнений?у=8х-3х3у=4х+58х2 -81
- 28. 3) Как с помощью графиков можно определить
- 29. 4) Можно ли найти решения данного уравнения?
- 30. Закрепление материала:1. В электронной таблице найти количество
- 31. 3. Найти количество корней системы уравнений, не
- 32. 5) Где быстрее строятся графики: в тетради
- 33. Задание на дом:1. Найти количество решений систем
Слайд 2Повторение, алгебра:
Свойства и графики функций:
Линейная функция: у = Kх+b
х
х
у
у
К>0, b
x = a, a>0
Слайд 3Свойства и графики функций:
у = ах2 + bх +с
a >0, D=0
a
x
x
x
x
y
y
y
y
a >0, D=0, b=c=0
a <0, D<0
Слайд 7
х
х
у
у
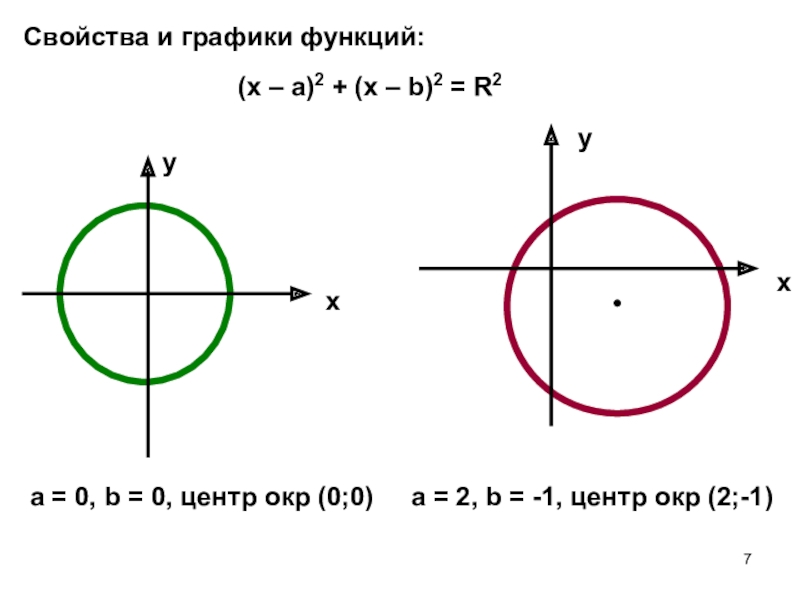
(х – а)2 + (х – b)2 = R2
a = 0,
a = 2, b = -1, центр окр (2;-1)
Свойства и графики функций:
Слайд 81.У=3,7+2,5х–5х3
2.У=3,7+2,5х–5х2
3.У = 3,7+2,5х
4.У = I3,7+2,5хI
А
Для какой функции построили график в электронной
ТЕСТ
Слайд 91.У=3,7+2,5х–5х3
2.У=3,7+2,5х–5х2
3.У = 3,7+2,5х
4.У = I3,7+2,5хI
Б
Для какой функции построили график в электронной
Слайд 101.У=3,7+2,5х–5х3
2.У=3,7+2,5х–5х2
3.У = 3,7+2,5х
4.У = I3,7+2,5хI
В
Для какой функции построили график в электронной
Слайд 114.У = I3,7+2,5хI
1.У=3,7+2,5х–5х3
2.У=3,7+2,5х–5х2
3.У = 3,7+2,5х
Г
Для какой функции построили график в электронной
Слайд 122) у = х2 - 4х - 5
1) у = 3х
В тетрадях схематически изобразите графики этих функций.
7) (х + 3)2 + (х – 2)2 = 16
Слайд 17Зная, что прямая х=0 – ось симметрии данного графика, какая из
1)
2)
Слайд 18Зная, что точка (0;0) – точка симметрии данного графика, какая из
1)
2)
Слайд 19ТЕСТ
Какие формулы, написанные при построении графиков в электронной таблице, соответствуют функциям:
1)
2) У=5х2+2х–7
3) У = 7+5х
4) У = I7-5хI
г) =5+2*D2-7*D2^3
е) =abs(7 -5*D2)
б) =7+5*D2
д) =5*D2^2+2*D2-7
в) =7+(D2-2)^2
а) =sqrt(5*D2-7)
ОТВЕТ: 1 - Г, 2 - Д, 3 - б, 4 - е, 5 - в, 6 - а
Слайд 20Расставьте по порядку алгоритм построения графика функции у = 2х3 –
А)
Б)
В)
Г)
Д)
Ответ: Б, В, Д, Г, А.
Слайд 21У=
Почему в электронной таблице в ходе построения графика в таблице
Какой из двух графиков соответствует данной функции? Для построения этого графика как надо выделить диапазон, чтобы график получился правильным?
1)
2)
Слайд 23Как вы думаете, сколько раз пересекаются эти графики?
Что нужно сделать при
А при построении в тетради?
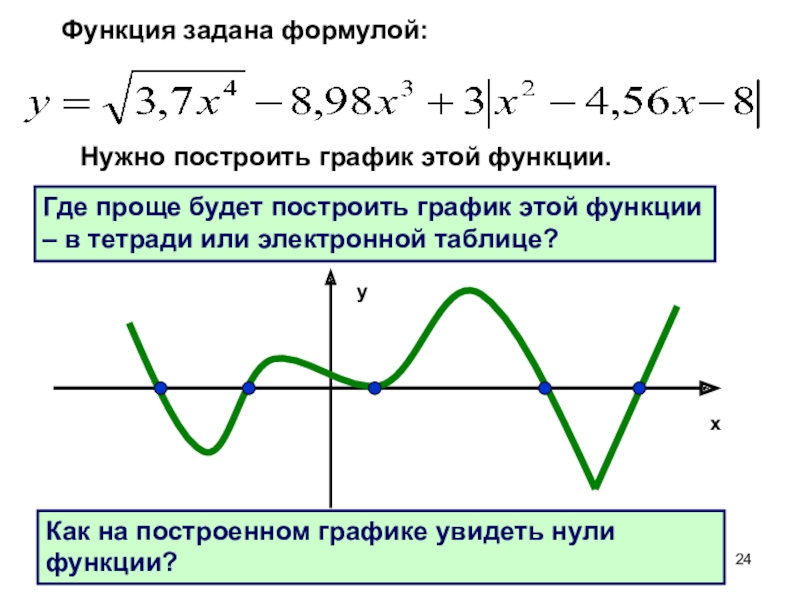
Слайд 24Функция задана формулой:
Нужно построить график этой функции.
Где проще будет построить
Как на построенном графике увидеть нули функции?
x
y
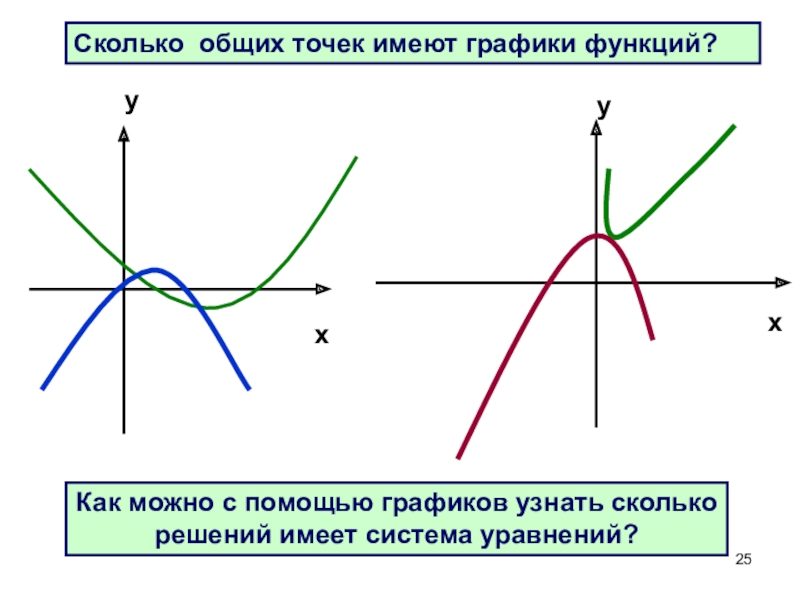
Слайд 25Сколько общих точек имеют графики функций?
Как можно с помощью графиков узнать
x
x
y
y
Слайд 26Объяснение материала: Решаются задачи в электронной таблице:
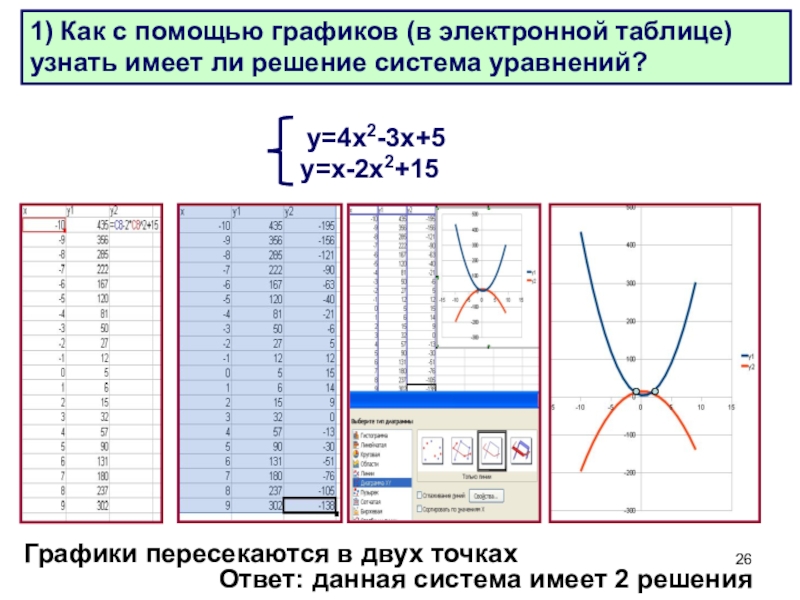
у=4х2-3х+5
у=х-2х2+15
Ответ: данная система имеет 2
Графики пересекаются в двух точках
1) Как с помощью графиков (в электронной таблице) узнать имеет ли решение система уравнений?
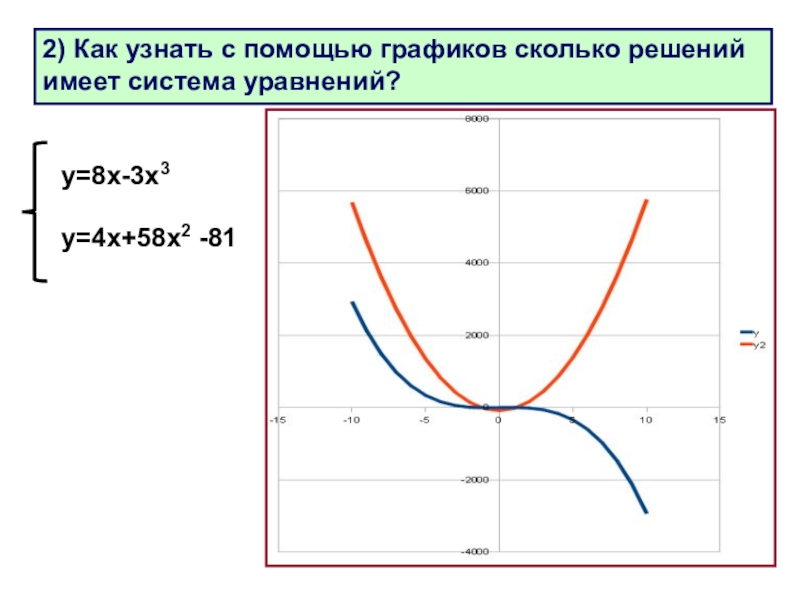
Слайд 272) Как узнать с помощью графиков сколько решений имеет система уравнений?
у=8х-3х3
у=4х+58х2
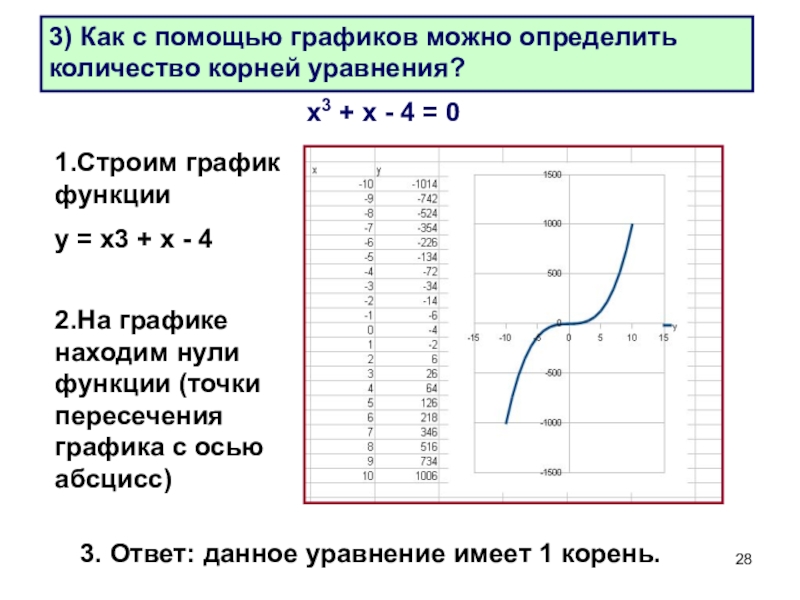
Слайд 283) Как с помощью графиков можно определить количество корней уравнения?
х3 +
1.Строим график функции
у = х3 + х - 4
2.На графике находим нули функции (точки пересечения графика с осью абсцисс)
3. Ответ: данное уравнение имеет 1 корень.
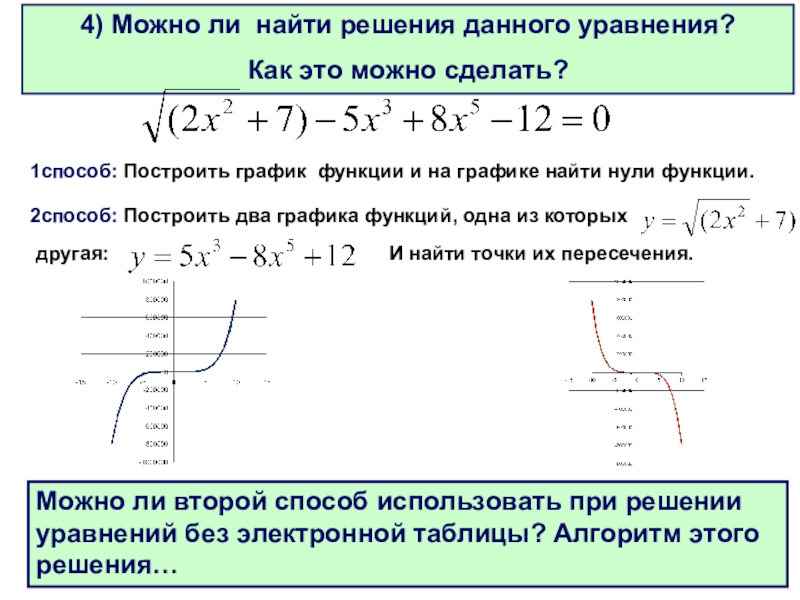
Слайд 294) Можно ли найти решения данного уравнения?
Как это можно сделать?
1способ:
2способ: Построить два графика функций, одна из которых
другая:
И найти точки их пересечения.
Можно ли второй способ использовать при решении уравнений без электронной таблицы? Алгоритм этого решения…
Слайд 30Закрепление материала:
1. В электронной таблице найти количество корней системы уравнений:
2. Сколько
у = 4,2х3 – 3,8х
у = (х – 1)4 – 210
у = 59 - 6,7х2 + 8х
у = I4,5х – 8,9I
б) 4 + 2х3 – х5 = 0
а) х3 – 6х +2 = 0
Слайд 313. Найти количество корней системы уравнений, не используя электронную таблицу (
4. Найти количество корней уравнения, не используя электронную таблицу
б)
а)
а) 2(х – 3)3 – (х +1)2 - 4 = 0
у = 2(х – 3)3 +1
(х + 1)2 + (у - 2)2 =25
у = -(х + 3)2 +2
y = I2х +5I
б) (х – 2)2 + (у +3) 2 – 15 - 2х = 0
Слайд 325) Где быстрее строятся графики: в тетради или электронной таблице?
6) Что
7) Что нужно знать о построении графиков функций, если электронной таблицей нельзя пользоваться?
Слайд 33Задание на дом:
1. Найти количество решений систем уравнений.
у = 4х4 –
у = (х – 1)3 +10
у = 9 - 6х3 + 5х
у = I5,6х + 4,1I
а) 2х3 – 9х +8 = 0
б) 17 + 12х2 – х4 = 0
2. Найти количество корней уравнения.
б)
а)
3. Схематически изобразив графики функций, найдите количество решений а) системы уравнений, б)уравнения
а)
б)
у = 2(х + 1)2 - 3
у = -(х - 1)3