- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Технологии табличных вычислений
Содержание
- 1. Презентация по информатике на тему Технологии табличных вычислений
- 2. Табличный процессор Табличные вычисления имеют
- 3. Табличный процессор Табличный процессор
- 4. Структура ЭТ и типы данных
- 5. Система имен – RC Для
- 6. Информация в ячейке ЭТ Информация
- 7. Числа в ЭТ Для записи
- 8. ЗаданиеПеревести числа в числа с фиксированной
- 9. Формулы в ЭТФормула определяет действия табличного
- 10. Приоритеты выполнения операций Формула определяет
- 11. ЗаданиеЗаписать в виде формулы электронной таблицы
- 12. Пример Вычислить площадь треугольника по формуле
- 13. Механизм перерасчета данных Исходными данными для
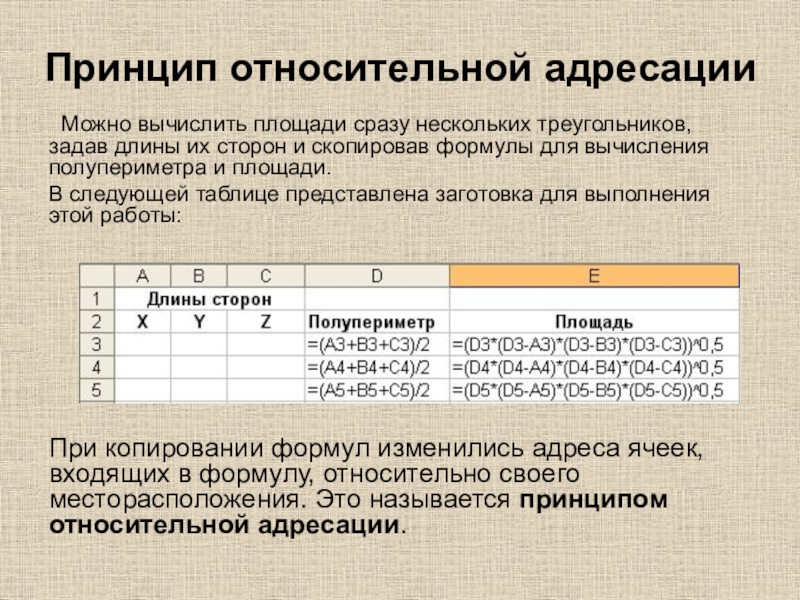
- 14. Принцип относительной адресации Можно вычислить
- 15. Абсолютная адресация В некоторых случаях
- 16. Пример Пусть длины сторон треугольника
- 17. В ячейке D3 электронной таблицы записана формула
- 18. Дан фрагмент электронной таблицы. Из ячейки D2
- 19. ЗаданиеСкопировать клетку B1 в B2 и B3, а клетку C1 - в C2,C3 и D1.
- 20. ЗаданияЧисловая константа 300 000 может быть записана
- 21. Задание
- 22. ЗаданиеВ клетку B1 электронной таблицы занесена
- 23. ЗаданиеВ электронной таблице при копировании содержимого
- 24. ЗаданиеДан фрагмент электронной таблицы в режиме
- 25. ДЗП. 3.3.1, уметь отвечать на вопросы
Слайд 2
Табличный процессор
Табличные вычисления имеют место в повседневной профессиональной
Для организации табличных расчетов применяют прикладные программы, называемые табличными процессорами.
Первый табличный процессор (VisiCalc) появился в 1979 году и был предназначен для персонального компьютера Apple-2.
Слайд 3
Табличный процессор
Табличный процессор реализует табличные вычисления, деловую
Слайд 4
Структура ЭТ и типы данных
При организации табличных вычислений
Строки пронумерованы.
Столбцы обозначены буквами латинского алфавита.
Имя ячейки состоит из названия столбца и номера строки, на пересечении которых она находится.
Имя ячейки также называют ее адресом: A1, AZ12.
Слайд 5
Система имен – RC
Для идентификации (обозначения) ячеек
Такое название произошло от английских слов Row (Строка) и Column (Столбец).
Например, адрес ячейки R12C4 в этой системе обозначений будет соответствовать ячейке D12, т.е. после буквы R указывается номер строки, а после буквы С – номер столбца, на пересечении которых располагается ячейка ЭТ.
Для работы в системе обозначений RC надо выполнить команду Сервис – Параметры – вкладка Общие.
Слайд 6
Информация в ячейке ЭТ
Информация заносится пользователем в ячейки
В каждую ячейку могут быть занесены текст, число или формула.
Тексты используются для оформления таблицы (надписи, заголовки, пояснения).
Слайд 7
Числа в ЭТ
Для записи чисел используются две формы:
Обычная форма предполагает, что целая часть отделена от дробной разделителем (точкой или запятой): 123.01 25 3,14.
Экспоненциальная форма, как правило, используется для записи очень больших или очень маленьких чисел.
Экспоненциальная форма числа содержит мантиссу, после которой идет буква E и порядок. Числовая константа в экспоненциальной форме трактуется как мантисса, умноженная на 10 в степени, равной порядку, то есть:
mEp=m*10p
Одно и то же число можно представить в разных формах: 5,3E2; 0,53E3; 5300E-1 и т.д. Если порядок числа положительный, то десятичная запятая переносится на p позиций вправо, а если отрицательный - то влево.
Нормализованная экспоненциальная форма - это форма, в которой целая часть числа мантиссы равна 0, а первая цифра после десятичной запятой - не 0. В нормализованной форме представлены числа: 0,53E3; 0,79E; 0,5E-1.
Слайд 8
Задание
Перевести числа в числа с фиксированной точкой: 1,3E-2; 15,64E3; 0,005E4.
Перевести
Слайд 9
Формулы в ЭТ
Формула определяет действия табличного процессора при реализации вычислений.
Формулы
- числа,
- имена ячеек,
- знаки операций,
- круглые скобки,
- имена функций.
Слайд 10
Приоритеты выполнения операций
Формула определяет действия табличного процессора при
При записи формул необходимо учитывать последовательность выполнения действий.
Если в записи формул отсутствуют скобки (вычисления в скобках выполняются в первую очередь), то операции выполняются в порядке старшинства:
^ – возведение в степень;
* и / – умножение и деление;
+ и - – сложение и вычитание.
Вся формула пишется в одну строку, проставляются все знаки операций.
Слайд 11
Задание
Записать в виде формулы электронной таблицы следующее арифметическое выражение:
Записать в
Слайд 12
Пример
Вычислить площадь треугольника по формуле Герона, зная длины его
Для решения задачи необходимо подготовить таблицу:
Слайд 13
Механизм перерасчета данных
Исходными данными для решения задачи являются длины
Таким образом, в ЭТ действует механизм перерасчёта при изменении исходных данных для формул.
Слайд 14
Принцип относительной адресации
Можно вычислить площади сразу нескольких треугольников,
В следующей таблице представлена заготовка для выполнения этой работы:
При копировании формул изменились адреса ячеек, входящих в формулу, относительно своего месторасположения. Это называется принципом относительной адресации.
Слайд 15
Абсолютная адресация
В некоторых случаях необходимо отменить принцип относительной
При относительной адресации при копировании или перемещении формулы слева направо или справа налево меняется имя столбца, а при копировании или перемещении формулы снизу вверх или сверху вниз - номер строки. При абсолютной адресации никаких изменений в формулах не происходит.
Абсолютная адресация используется, если в различных клетках таблицы необходимо ссылаться на одно и то же значение. Тогда это значение удобно хранить в одной из клеток таблицы как константу, а в остальных клетках ссылаться на адрес этой клетки.
Слайд 16
Пример
Пусть длины сторон треугольника заданы в дециметрах. Вычислить
При копировании формулы, вычисляющей площадь треугольника, адрес ячейки Е1 должен оставаться неизменным.
Слайд 17В ячейке D3 электронной таблицы записана формула =B$2+$B3. Какой вид приобретет
Примечание: знак $ используется для обозначения абсолютной адресации.
1) =C$2+$B4
2) =A$2+$B1
3) =B$3+$C3
4) =B$1+$A3
Решение.
B$2: меняется столбец и не меняется номер строки.
$B3: столбец не меняется, меняется номер строки.
Номер столбца Е больше номера столбца D на 1. Значит, столбец B станет столбцом С.
Номер строки 4 на 1 больше номера строки 3, значит, строка 3 станет строкой 4.
Окончательный вид =С$2+$B4.
Правильный ответ указан под номером 1.
Слайд 18Дан фрагмент электронной таблицы. Из ячейки D2 в одну из ячеек
Примечание.
Знак $ обозначает абсолютную адресацию.
Решение.
При копировании формулы из ячейки D2 у первого слагаемого может изменяться
только номер столбца, а у второго — только номер строки.
Таким образом формулы в ячейках E1—E4:
E1 = C$3+$C1 = 8 E2 = C$3+$C2 = 9 E3 = C$3+$C3 = 10 E4 = C$3+$C4 = 11.
Таким образом, формула была скопирована в ячейку E1.
Ответ: 1.
Слайд 20
Задания
Числовая константа 300 000 может быть записана в виде:
1
4 30,0E+5 5 0,3E+5
Числовая константа 2,3Е–2 может быть записана в виде:
1 0,0023 2 –2,3 3 0,023
4 –0,0023 5 230,0
Слайд 22
Задание
В клетку B1 электронной таблицы занесена формула =0,314E+1*2*A1. Чему будет
1 формула будет воспринята как текст, и вычисления производиться не будут
2 12,314 3 37,68
4 3,768 5 15,14
Слайд 23
Задание
В электронной таблице при копировании содержимого клетки A2 в клетки
1 =$A$1+B1 2 =$A1+B1
3 =$A1+C1 4 =$A$1+C1
5 =A1+B1
Слайд 24
Задание
Дан фрагмент электронной таблицы в режиме отображения формул. В клетки
1 10 и 20 2 20 и 30 3 20 и 20
4 0 и 0 5 10 и 10