- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Основы логики: логические величины и формулы
Содержание
- 1. Презентация по информатике на тему Основы логики: логические величины и формулы
- 2. ВЫСКАЗЫВАНИЕ - это повествовательное предложение, о котором
- 3. Какие из предложений являются высказываниями? Определите их
- 4. Высказывания могут быть простыми и сложными.Высказывание считается
- 5. Высказывание, которое можно разложить на части, называется
- 6. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ«Сегодня светит солнце и идет дождь»А
- 7. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЪЮНКЦИЯ)Обозначение: &, ^, *.Союз в
- 8. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ«На стоянке находится «Мерседес» или «Жигули»А
- 9. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ)Обозначение: +, V.Союз в естественном
- 10. ЛОГИЧЕСКОЕ ОТРИЦАНИЕА – «Сегодня светит солнце»В –
- 11. ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ)Обозначение: ¬.Союз в естественном языке:
- 12. Слайд 12
- 13. Определите последовательность операций:не А или не В
- 14. Пусть а, b, с — логические величины, которые имеют
- 15. Домашнее заданиеПостройте таблицы истинности для логических из предыдущего задания.
Слайд 2ВЫСКАЗЫВАНИЕ - это повествовательное предложение, о котором можно сказать, что оно
Например:
Земля - планета Солнечной системы.
2+8<5
5 · 5=25
Всякий квадрат есть параллелограмм
Каждый параллелограмм есть квадрат
(Истинно)
(Ложно)
(Истинно)
(Истинно)
(Ложно)
Слайд 3Какие из предложений являются высказываниями? Определите их истинность.
Число (- 12) –
Добрый вечер!
Число 11 является простым.
Кто отсутствует?
Лед – твердое состояние руды.
Выразите 1кг 15 грамм в граммах.
Я – последняя буква в алфавите.
Сложите числа 2 и 5.
Какой длины эта веревка?
Треугольник – геометрическая фигура.
Прослушайте сообщение.
Назовите устройство ввода информации.
У каждой лошади есть хвост.
Париж - столица Ирландии.
14 + 3 = 10.
Некоторые медведи живут на севере.
Слайд 4Высказывания могут быть простыми и сложными.
Высказывание считается простым, если никакую его
Например:
На улице идет дождь.
На улице светит солнце.
На улице пасмурная погода.
Слайд 5Высказывание, которое можно разложить на части, называется сложным
Сложное высказывание получается путем
Например, даны простые высказывания:
На улице идет дождь.
На улице светит солнце.
На улице пасмурная погода.
Составим из них сложные высказывания:
На улице идет дождь и на улице светит солнце.
На улице светит солнце или на улице пасмурная погода.
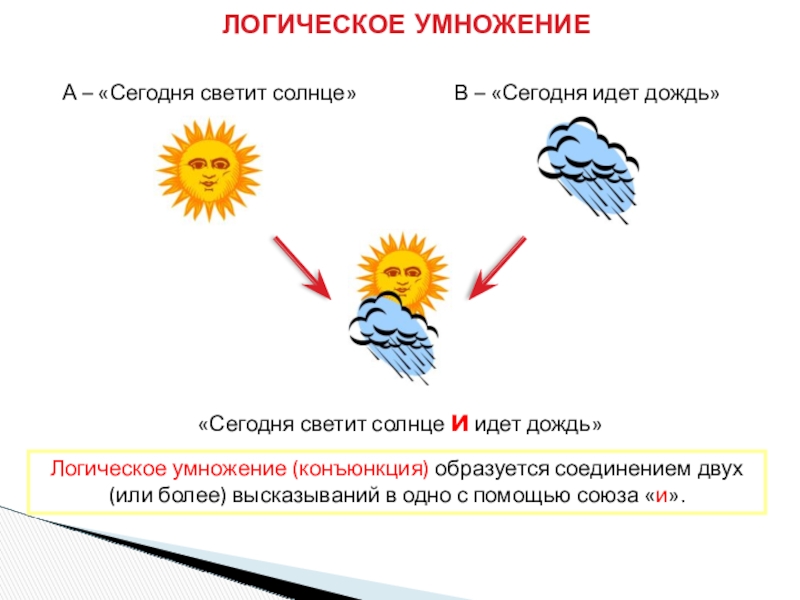
Слайд 6ЛОГИЧЕСКОЕ УМНОЖЕНИЕ
«Сегодня светит солнце и идет дождь»
А – «Сегодня светит солнце»
В
Логическое умножение (конъюнкция) образуется соединением двух (или более) высказываний в одно с помощью союза «и».
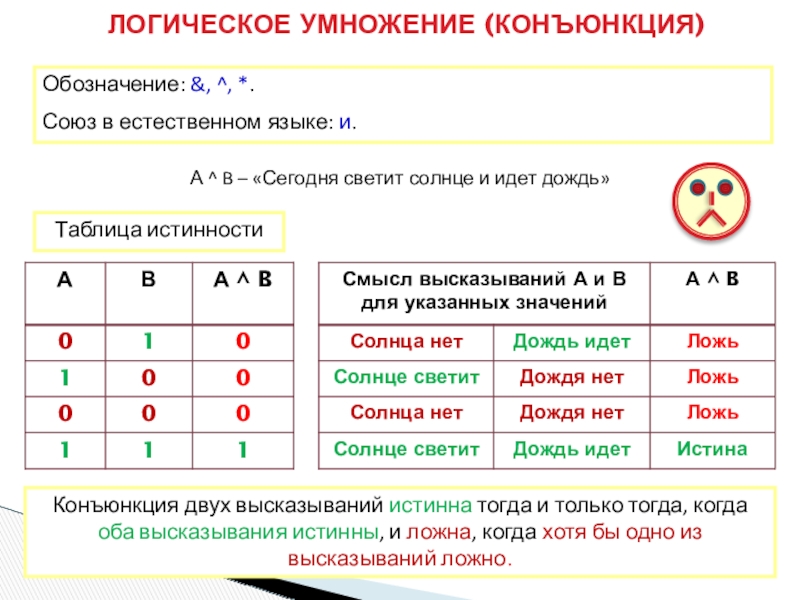
Слайд 7ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЪЮНКЦИЯ)
Обозначение: &, ^, *.
Союз в естественном языке: и.
А ^
Таблица истинности
Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно из высказываний ложно.
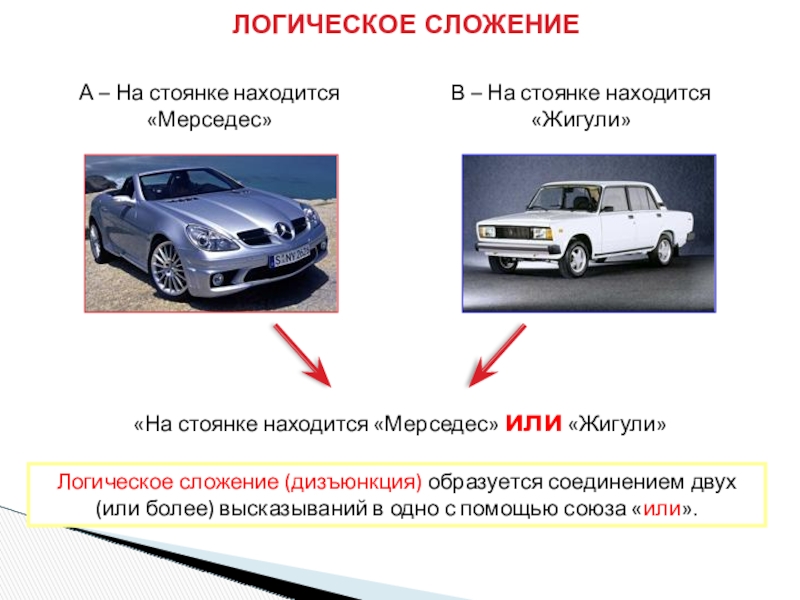
Слайд 8ЛОГИЧЕСКОЕ СЛОЖЕНИЕ
«На стоянке находится «Мерседес» или «Жигули»
А – На стоянке находится
В – На стоянке находится «Жигули»
Логическое сложение (дизъюнкция) образуется соединением двух (или более) высказываний в одно с помощью союза «или».
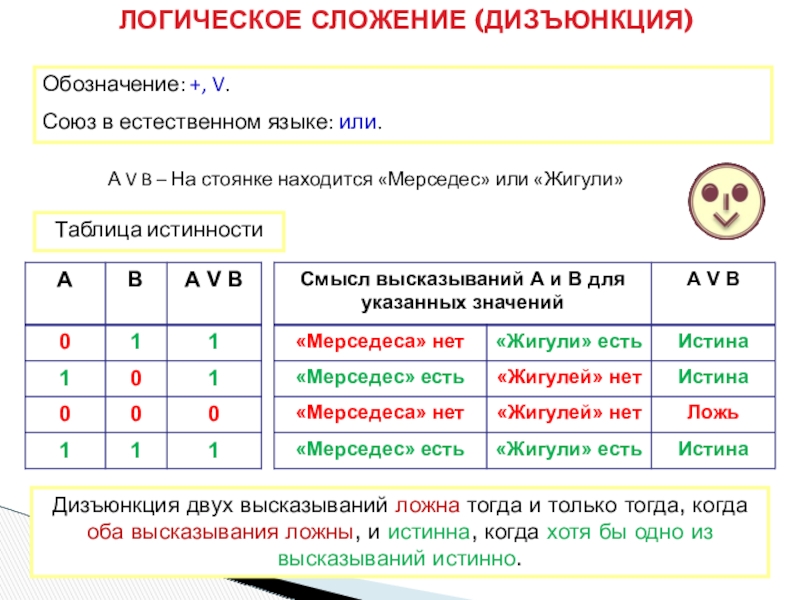
Слайд 9ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ)
Обозначение: +, V.
Союз в естественном языке: или.
А V B
Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно из высказываний истинно.
Таблица истинности
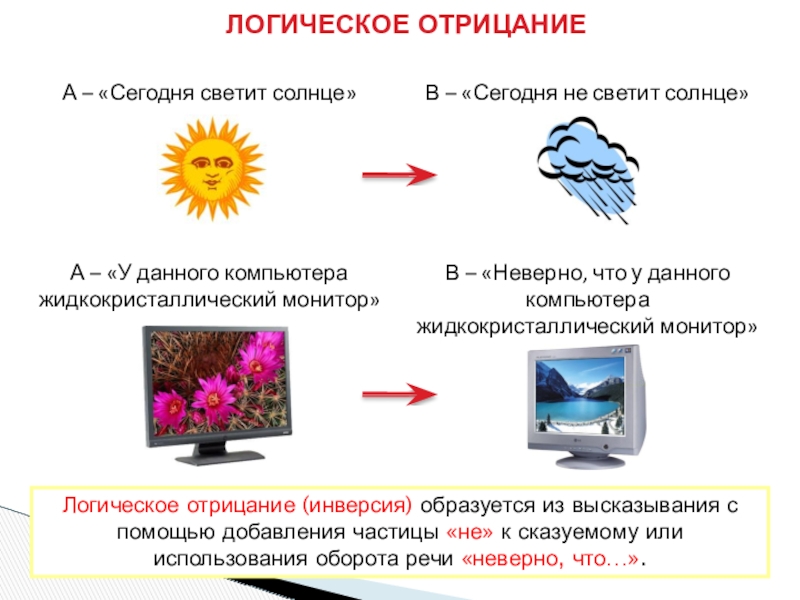
Слайд 10ЛОГИЧЕСКОЕ ОТРИЦАНИЕ
А – «Сегодня светит солнце»
В – «Сегодня не светит солнце»
Логическое
А – «У данного компьютера жидкокристаллический монитор»
В – «Неверно, что у данного компьютера жидкокристаллический монитор»
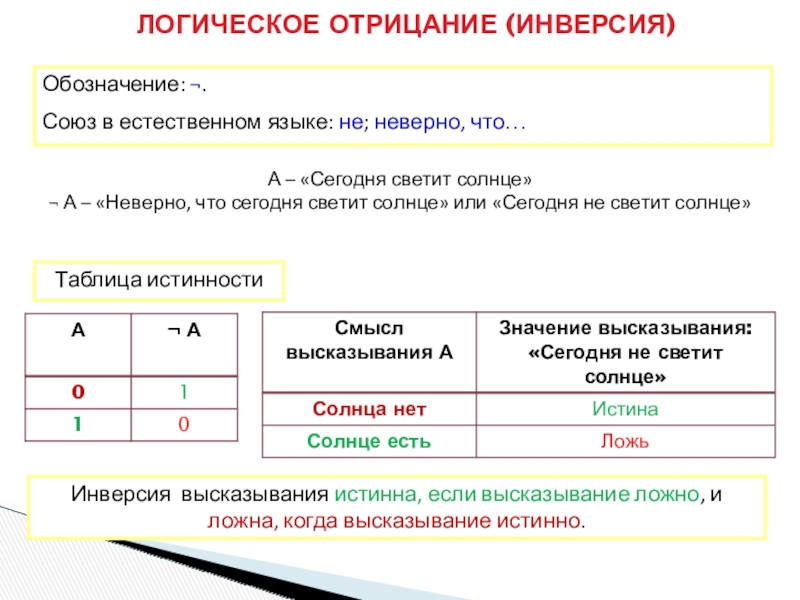
Слайд 11ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ)
Обозначение: ¬.
Союз в естественном языке: не; неверно, что…
А –
¬ А – «Неверно, что сегодня светит солнце» или «Сегодня не светит солнце»
Инверсия высказывания истинна, если высказывание ложно, и ложна, когда высказывание истинно.
Таблица истинности
Слайд 13Определите последовательность операций:
не А или не В
А или В и
А и В или С
(А или В) и С или не А
Слайд 14Пусть а, b, с — логические величины, которые имеют следующие значения: а = ИСТИНА,
1) а и b; 2) а или b; 3) не а или b; 4) а и b или с; 5) а или b и с; 6) не а или b и с; 7) (а или b) и (с или b); 8) не (а или b) и (с или b); 9) не (а и b и с).