- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Логика (8 класс)
Содержание
- 1. Презентация по информатике на тему Логика (8 класс)
- 2. Этапы развития логикиПервые учения о формах и
- 3. В XVII веке немецкий ученый и философ
- 4. Если бы компьютер умел только быстро вычислять,
- 5. ВысказываниеВысказывание – это грамматически правильное повествовательное предложение,
- 6. Выражения, не являющиеся высказываниями
- 7. Выполните задания:№1 Какие из следующих предложений являются
- 8. №2 Какие из приведенных высказываний являются общими,
- 9. Логические выраженияАлгебра логики – наука об операциях
- 10. Логические операцииОтрицание (инверсия) – операция НЕ.Логическая операция
- 11. Примеры.Высказывание «Число 10 – четное» - истина
- 12. Логическое умножение(конъюнкция) – операция И.Логическая операция И
- 13. Примеры.Рассмотрим высказывание «Число 10 – четное и
- 14. Логическое сложение(дизъюнкция) – операция ИЛИ.Логическая операция ИЛИ
- 15. Примеры.Рассмотрим высказывание «В библиотеке можно взять книгу
- 16. Логическое следование (импликация) – операция «если-то».Импликация связывает
- 17. Примеры.Рассмотрим высказывание «Если идет дождь, то на
- 18. Эквивалентность -операция «А тогда и только тогда,
- 19. Примеры.«День сменяет ночь тогда и только тогда,
- 20. Выполните задания:№3 а) Из двух простых высказываний
- 21. №4 Определите значение истинности следующих высказываний:Приставка –
- 22. № 5 Пусть А=«эта ночь звездная»,
- 23. Запишите ¬Х, ¬У, Х&У, ¬Х∨ ¬ У:
- 24. Запишите высказывания в виде логических выражений: Я
- 25. Даны высказывания А = «5*10=60», В =
- 26. ЗадачиДля какого Х истинно высказывание((Х>2) ∨(Х4))?1) 1
- 27. ЗадачиДля какого слова истинно высказывание¬(Первая буква слова
- 28. Задание на дом:Для какого слова истинно высказывание(Первая
- 29. Таблицы истинностиРешение логических выражений принято записывать в
- 30. Символом F обозначено одно из указанных ниже
- 31. Ответ:4
- 32. Задание на дом:Символом F обозначено одно из
- 33. Ответ:1
- 34. Законы логики
- 35. Законы логики
- 36. РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ
- 37. Решение логических задачКак правило, логические задачи формулируются
- 38. Задача на смекалкуЧто получится, если сложить: начало
- 39. ОтветКонтроль
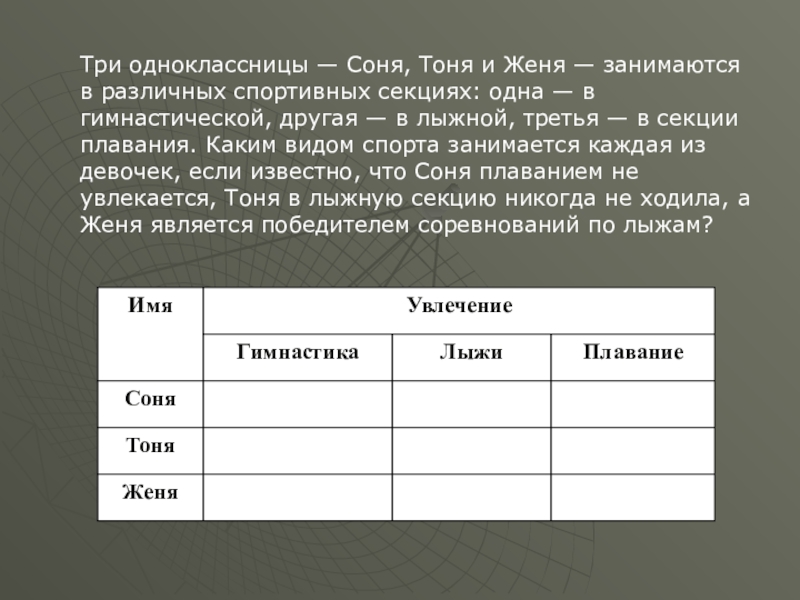
- 40. Три одноклассницы — Соня, Тоня и Женя
- 41. ОтветСоня занимается гимнастикой; Женя – лыжами; Тоня – Плаванием.
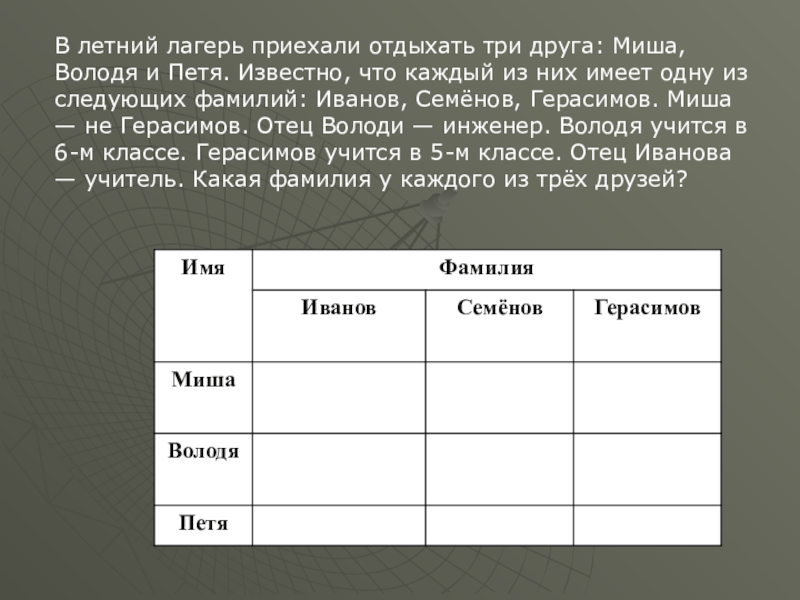
- 42. В летний лагерь приехали отдыхать три друга:
- 43. ОтветыМиша Иванов; Володя Семёнов; Петя Герасимов.
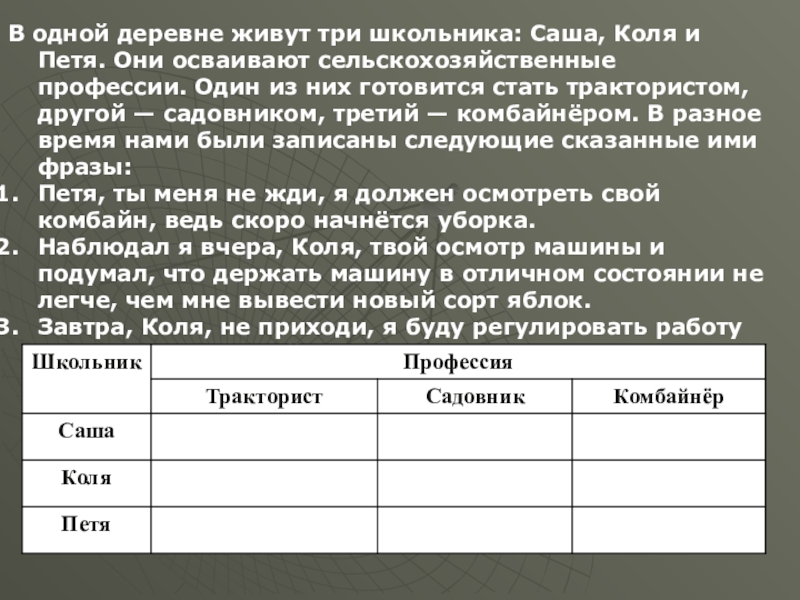
- 44. В одной деревне живут три школьника: Саша,
- 45. ОтветыСаша овладевает профессией комбайнёра; Коля – тракториста; Петя – садовника.
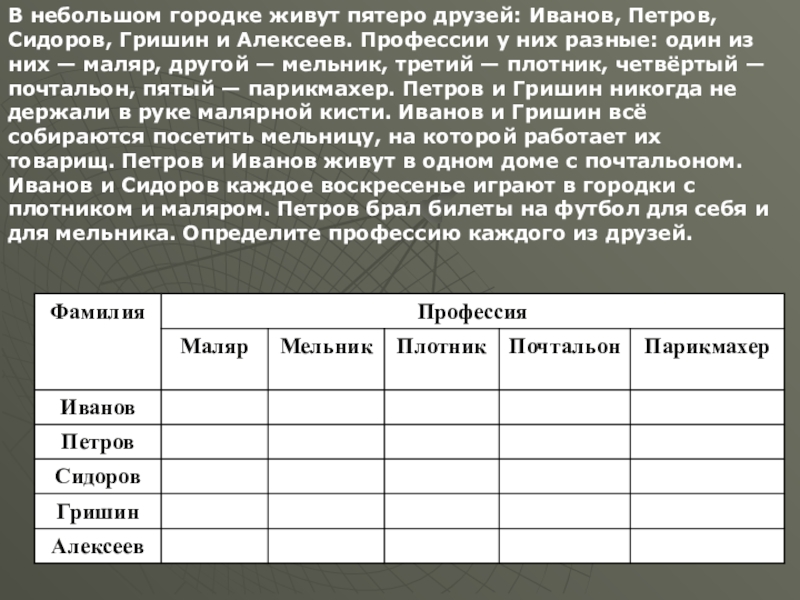
- 46. В небольшом городке живут пятеро друзей: Иванов,
- 47. Ответы У Иванова профессия парикмахер, у Петрова
- 48. Три молодых человека – Андрей, Бронислав и
- 49. Ответы Андрей агроном живет в АрхангельскеБронислав аптекарь живет в БобруйскеБорис бухгалтер живет в Белгороде
- 50. ЗАДАЧА 1. Разбирается дело Лёнчика, Пончика и
- 51. Задача 2.В школьном первенстве по настольному теннису
- 52. Задача 3.Вадим, Сергей и Михаил изучают различные
- 53. Задача 4.Три молодые мамы Анна, Ирина, Ольга,
Слайд 2Этапы развития логики
Первые учения о формах и способах рассуждений возникли в
Слайд 3 В XVII веке немецкий ученый и философ Готфрид Вильгельм Лейбниц (1646
На фундаменте, заложенном Лейбницем, другой великий математик, англичанин Джордж Буль (1815-1864) воздвиг здание новой области науки – математической логики.
Начальный раздел математической логики называют алгеброй логики или Булевой алгеброй.
Слайд 4
Если бы компьютер умел только быстро вычислять, то он был бы
Логика (от греч. Logos – слово , понятие, рассуждение, разум) – наука о законах и формах правильного мышления.
Логически правильный вывод позволяет из имеющихся истин получать новые истины с помощью чистого рассуждения, без обращения к опыту, интуиции.
В формальной логике правильность рассуждения зависит только от его формы и не зависит от конкретного содержания.
Формальная логика содержит в себе некоторые основные понятия, такие как: высказывание, истинность высказывания и вывод.
Слайд 5Высказывание
Высказывание – это грамматически правильное повествовательное предложение, относительно которого имеет смысл
Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Ложным высказывание будет в том случае, когда оно противоречит реальной действительности.
Например,
истинное высказывание: «Москва – столица России»,
ложное высказывание: «Компьютер был изобретен в XIX в».
Высказывания бывают:
общие (начинается или можно начать со слов :все , всякий, каждый, ни один). «Все рыбы умеют плавать»;
частные (начинается или можно начать со слов : некоторые, большинство). «Некоторые медведи – бурые»;
единичные (во всех других случаях). «Буква А – гласная».
Слайд 7Выполните задания:
№1 Какие из следующих предложений являются высказываниями? Определите их истинность.
Число
Посмотрите на доску.
У каждой лошади есть хвост.
Внимание!
Кто отсутствует?
Есть кошки, которые дружат с собаками.
Х2>0.
4+5=10.
Число 11 является простым.
Некоторые люди являются художниками.
Париж – столица Англии.
Сложите числа 2 и 5.
Все медведи – бурые.
Некоторые медведи живут на севере.
Выразите 1ч 15 мин. в минутах.
Полярная звезда находится в созвездии Малой Медведицы.
Не нарушайте правил дорожного движения.
Слайд 8№2 Какие из приведенных высказываний являются общими, какие частными, какие единичными?
Не
Кошка является домашним животным.
Все солдаты храбрые.
Ни один внимательный человек не совершит оплошность.
Некоторые ученики двоечники.
Все ананасы приятны на вкус.
Мой кот страшный забияка.
Некоторые мои друзья собирают марки.
Все лекарства неприятны на вкус.
А – первая буква в алфавите.
Тигр – хищное животное.
У некоторых змей нет ядовитых зубов.
Многие растения обладают целебными свойствами.
Все металлы проводят тепло.
Некоторые рыбы - хищники.
Слайд 9Логические выражения
Алгебра логики – наука об операциях над высказываниями.
Логическая переменная -
Логическое выражение - простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операций.
Слайд 10Логические операции
Отрицание (инверсия) – операция НЕ.
Логическая операция НЕ применяется к одному
Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.
Записывается в виде :
Таблица истинности:
Слайд 11Примеры.
Высказывание «Число 10 – четное» - истина
Высказывание «Неверно, что число 10
Высказывание «Число 10 - отрицательное» - ложно Высказывание «Неверно, что число 10 - отрицательное» - истина
Принцип работы переключателя настольной лампы таков: если лампа горела, переключатель выключает ее, если лампа не горела – включает ее. Такой переключатель можно считать электрическим аналогом операции отрицания.
Слайд 12Логическое умножение(конъюнкция) – операция И.
Логическая операция И пересекает два высказывания, в
Результат операции И истинен тогда и только тогда, когда оба исходных выражения истинны, и ложным в остальных случаях.
Записывается в виде : А&В, А∧В
Таблица истинности:
Слайд 13Примеры.
Рассмотрим высказывание «Число 10 – четное и целое». Это высказывание формально
Логическую операцию И можно сравнить с последовательным соединением лампочек в гирлянде. При наличии хотя бы одной неработающей лампочки электрическая цепь оказывается разомкнутой, то есть гирлянда не работает. Ток протекает только при одном условии – все составляющие цепи должны быть исправны.
Слайд 14Логическое сложение(дизъюнкция) – операция ИЛИ.
Логическая операция ИЛИ объединяет два высказывания, в
Результат операции ИЛИ ложным тогда и только тогда, когда оба выражения ложны, и истинным в остальных случаях.
Записывается в виде : А∨В
Таблица истинности:
Слайд 15Примеры.
Рассмотрим высказывание «В библиотеке можно взять книгу или встретить знакомого». Это
высказывание А - «В библиотеке можно взять книгу»,
а высказывание В - «В библиотеке можно встретить знакомого». Объединение этих высказываний при помощи операции логического сложения означает, что события могут произойти как отдельно, так и одновременно.
Логическую операцию ИЛИ можно сравнить с параллельным соединением лампочек в гирлянде. Такая гирлянда будет светить до тех пор, пока цела хотя бы одна лампочка. Результат операции ложь будет только в одном случае – когда все аргументы ложны.
Слайд 16Логическое следование (импликация) – операция «если-то».
Импликация связывает два простых логических выражения,
Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
Записывается в виде : А→В
Таблица истинности:
Слайд 17Примеры.
Рассмотрим высказывание «Если идет дождь, то на улице сыро». Это высказывание
высказывание А - «Идет дождь»,
а высказывание В - «На улице сыро».
Высказывание «Если не идет дождь, то на улице не сыро» - истинно.
На улице может быть сыро и без дождя, например, когда прошла поливочная машина или дождь прошел накануне.
Результат операции ложен тогда, когда дождь идет, а на улице не сыро.
Слайд 18Эквивалентность -
операция «А тогда и только тогда, когда В».
Результат операции эквивалентность
Записывается в виде : А↔В, А≡В
Таблица истинности:
Слайд 19Примеры.
«День сменяет ночь тогда и только тогда, когда солнце скрывается за
«Добиться результата в спорте можно тогда и только тогда, когда приложено максимум усилий».
Слайд 20Выполните задания:
№3 а) Из двух простых высказываний постройте сложное высказывание, используя
Например: Все ученики изучают математику.
Все ученики изучают литературу.
Получаем: Все ученики изучают математику и литературу.
Марина старше Светы. Оля старше Светы.
Одна половина класса изучает английский язык. Вторая половина класса изучает немецкий язык.
В кабинете есть учебники. В кабинете есть справочники.
Часть туристов любит чай. Остальные туристы любят молоко.
Синий кубик меньше красного. Синий кубик меньше зеленого.
Х=3, Х>2.
б) Используя связку «если…, то …», измените высказывания.
Например: Человек, любящий животных, - добрый.
Получаем: Если человек любит животных, то он - добрый.
Сделал дело - гуляй смело.
Переходи улицу только на зеленый свет.
Когда темнеет, зажигают фонари.
В високосном год 366 дней..
По стройке необходимо ходить в каске.
При встрече люди приветствуют друг друга.
Тише едешь – дальше будешь.
Слайд 21№4 Определите значение истинности следующих высказываний:
Приставка – это часть слова, и
Неверно, что 2х2=5
Суффикс – это часть слова, и он стоит после корня.
Родственные слова имеют общую часть, и она называется корнем.
Если Х – сын или дочь У, то У – мать или отец Х.
Рыбу ловят сачком или крючком, или мухой приманивают, иль червячком.
Неверно, что 5+5=10
Буква «а» - первая буква в слове «аист» или «сова».
Две прямые на плоскости параллельны или пересекаются.
Данное число четно или число, больше его на единицу, четно.
Если утром тучи в небе, то к обеду будет дождь.
Луна – планета или 2+2=5
Слайд 22№ 5 Пусть А=«эта ночь звездная»,
Выразите формулы на обычном языке:
А и В
А и не В
не А и не В
не А или В
не А и В
не А или не В
№ 6 Определите значения логических переменных А, В,С, если:
А или (1 литр молока дороже 1 кг сливочного масла) – истинно;
В и (1 литр молока дороже 1 кг сливочного масла) – ложно;
С или (масло дороже творога) – истинно;
А и (масло дороже творога) – ложно
А и (Марс – планета) – истинно;
В и (Марс – планета) – ложно;
С или (Солнце – спутник Земли) – истинно;
А или (Солнце – спутник Земли) – ложно
№ 7 Какое логическое выражение соответствует высказыванию:
«Точка Х принадлежит интервалу (А;В)»
(Х
(Х>A) и (X
Слайд 24Запишите высказывания в виде логических выражений:
Я поеду к бабушке в
Неверно, что если солнце светит, то ветер дует тогда и только тогда, когда идет дождь
Задание на дом:
Если будет светить солнце, то ребята пойдут гулять, а если пойдет дождь, то ребята останутся дома
Если учитель на уроке рассказывает интересно, то ни Маша, ни Саша, ни Аня не будут смотреть в окно
Слайд 25Даны высказывания
А = «5*10=60»,
В = «17+7=24».
Определите истинность высказываний:
1) А;
3) А∨В; 4) В;
5) А; 6) А&В.
Слайд 26Задачи
Для какого Х истинно высказывание
((Х>2) ∨(Х4))?
1) 1 2) 2
Задание на дом:
Для какого Х истинно высказывание
¬((Х>3) →(Х>4))?
1) 1 2) 2 3) 3 4)4
Слайд 27Задачи
Для какого слова истинно высказывание
¬(Первая буква слова согласная →(вторая буква слова
1) горе 2) привет 3) кресло 4)закон
Слайд 28Задание на дом:
Для какого слова истинно высказывание
(Первая буква слова гласная ∨
1) арбуз 2) ответ 3) кресло 4) привал
Слайд 29Таблицы истинности
Решение логических выражений принято записывать в виде таблиц истинности –
Приоритет выполнения логических операций следующий:
инверсия, конъюнкция, дизъюнкция.
Для составления таблицы необходимо:
Выяснить количество строк в таблице (вычисляется 2n+1, где n – количество переменных).
Выяснить количество столбцов = количество переменных + количество логических операций.
Установить последовательность выполнения логических операций.
Построить таблицу, указывая названия столбцов и возможные наборы значений логических переменных.
Заполнить таблицу истинности по столбцам.
Слайд 30Символом F обозначено одно из указанных ниже логических выражений от трех
Какое выражение соответствует F?
1)¬X ∧ ¬Y ∧ ¬Z
2) X ∧ Y ∧ Z
3) X ∨ Y ∨ Z
4) ¬X ∨ ¬Y ∨ ¬Z
Тема: Построение таблиц истинности логических выражений.
А9 образец
Слайд 32Задание на дом:
Символом F обозначено одно из указанных ниже логических выражений
1) X ∨ ¬Y ∨ Z
2) X ∧ Y ∧ Z
3) X ∧ Y ∧ ¬Z
4) ¬X ∨ Y ∨ ¬Z
Слайд 37Решение логических задач
Как правило, логические задачи формулируются на естественном языке. В
Внимательно изучить условие.
Выделить простые высказывания и обозначить их латинскими буквами.
Записать условие задачи на языке алгебры логики.
Составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения, приравнять произведение единице.
Упростить формулу.
Проанализировать полученный результат или составить таблицу истинности, найти по таблице значения переменных, для которых значение функции равно 1.
Записать ответ.
Слайд 38Задача на смекалку
Что получится, если сложить:
начало конца,
конец начала,
первое
хвост кота,
середину вторника,
перед осы,
начало леса
и конец ночи?
Слайд 40Три одноклассницы — Соня, Тоня и Женя — занимаются в различных
Слайд 42В летний лагерь приехали отдыхать три друга: Миша, Володя и Петя.
Слайд 44В одной деревне живут три школьника: Саша, Коля и Петя. Они
Петя, ты меня не жди, я должен осмотреть свой комбайн, ведь скоро начнётся уборка.
Наблюдал я вчера, Коля, твой осмотр машины и подумал, что держать машину в отличном состоянии не легче, чем мне вывести новый сорт яблок.
Завтра, Коля, не приходи, я буду регулировать работу молотилки у комбайна.
Слайд 46В небольшом городке живут пятеро друзей: Иванов, Петров, Сидоров, Гришин и
Слайд 47Ответы
У Иванова профессия парикмахер,
у Петрова – плотник,
у Сидорова
у Гришина – почтальон, у Алексеева – маляр.
Слайд 48Три молодых человека – Андрей, Бронислав и Борис живут в Бобруйске,
Борис бывает в Бобруйске лишь наездами и то весьма редко, хотя все его родственники живут в этом городе.
У двоих из этих людей названия профессий и городов , в которых они живут, начинаются с той же буквы, что и имена.
Жена аптекаря доводится Борису младшей сестрой.
Слайд 49Ответы
Андрей агроном живет в Архангельске
Бронислав аптекарь живет в Бобруйске
Борис бухгалтер
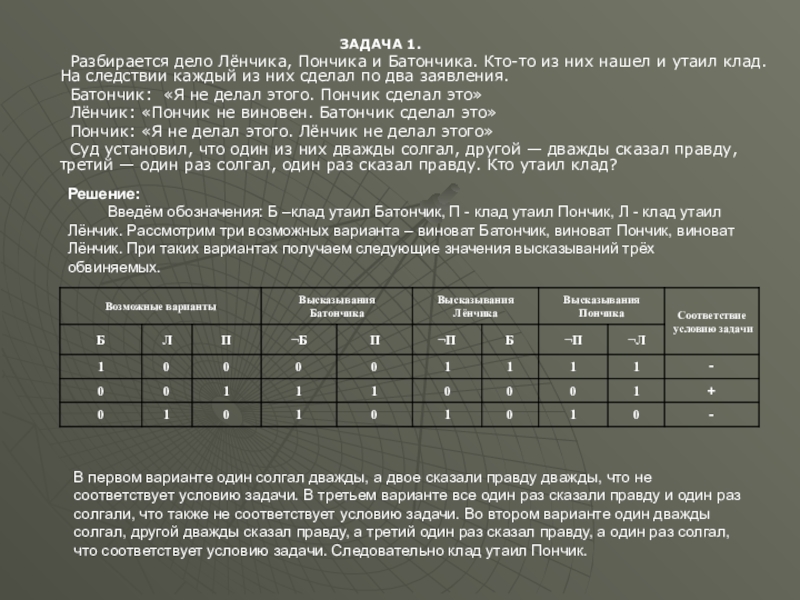
Слайд 50ЗАДАЧА 1.
Разбирается дело Лёнчика, Пончика и Батончика. Кто-то из них
Батончик: «Я не делал этого. Пончик сделал это»
Лёнчик: «Пончик не виновен. Батончик сделал это»
Пончик: «Я не делал этого. Лёнчик не делал этого»
Суд установил, что один из них дважды солгал, другой — дважды сказал правду, третий — один раз солгал, один раз сказал правду. Кто утаил клад?
В первом варианте один солгал дважды, а двое сказали правду дважды, что не соответствует условию задачи. В третьем варианте все один раз сказали правду и один раз солгали, что также не соответствует условию задачи. Во втором варианте один дважды солгал, другой дважды сказал правду, а третий один раз сказал правду, а один раз солгал, что соответствует условию задачи. Следовательно клад утаил Пончик.
Решение:
Введём обозначения: Б –клад утаил Батончик, П - клад утаил Пончик, Л - клад утаил Лёнчик. Рассмотрим три возможных варианта – виноват Батончик, виноват Пончик, виноват Лёнчик. При таких вариантах получаем следующие значения высказываний трёх обвиняемых.
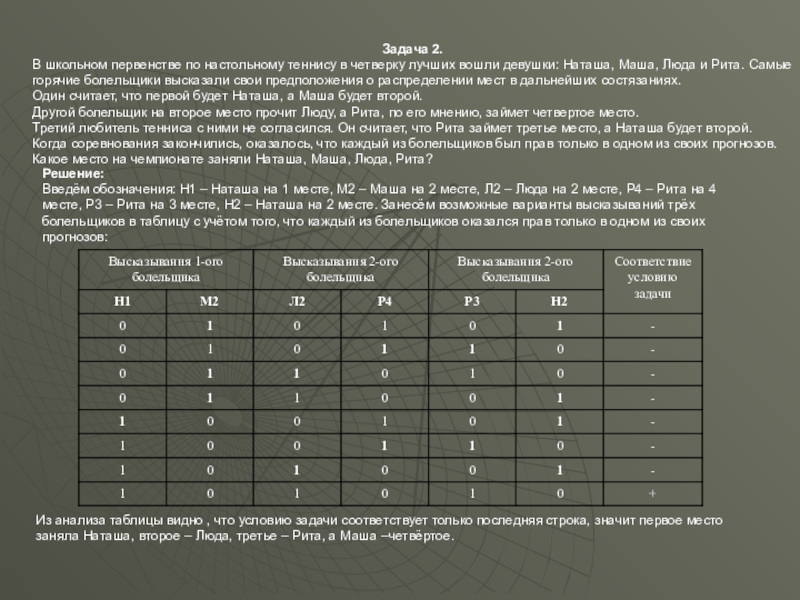
Слайд 51Задача 2.
В школьном первенстве по настольному теннису в четверку лучших вошли
Один считает, что первой будет Наташа, а Маша будет второй.
Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место.
Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?
Из анализа таблицы видно , что условию задачи соответствует только последняя строка, значит первое место заняла Наташа, второе – Люда, третье – Рита, а Маша –четвёртое.
Решение:
Введём обозначения: Н1 – Наташа на 1 месте, М2 – Маша на 2 месте, Л2 – Люда на 2 месте, Р4 – Рита на 4 месте, Р3 – Рита на 3 месте, Н2 – Наташа на 2 месте. Занесём возможные варианты высказываний трёх болельщиков в таблицу с учётом того, что каждый из болельщиков оказался прав только в одном из своих прогнозов:
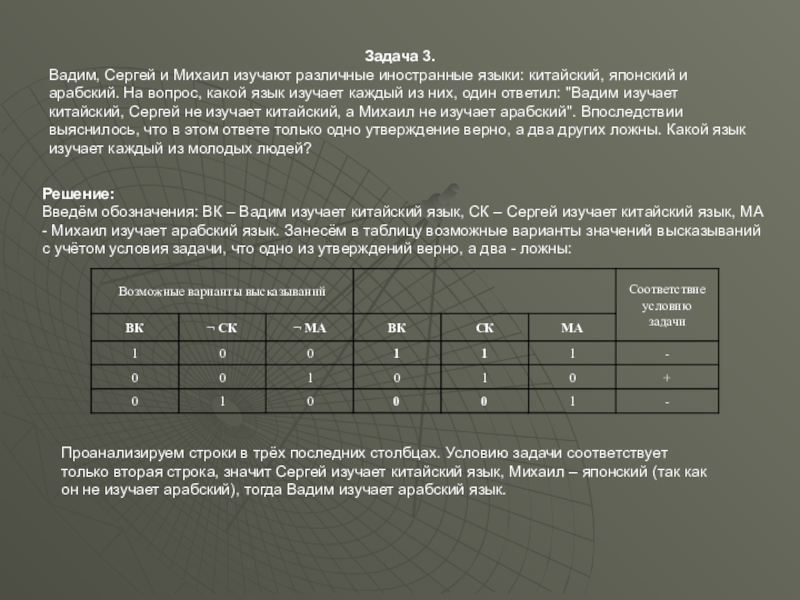
Слайд 52Задача 3.
Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский
Проанализируем строки в трёх последних столбцах. Условию задачи соответствует только вторая строка, значит Сергей изучает китайский язык, Михаил – японский (так как он не изучает арабский), тогда Вадим изучает арабский язык.
Решение:
Введём обозначения: ВК – Вадим изучает китайский язык, СК – Сергей изучает китайский язык, МА - Михаил изучает арабский язык. Занесём в таблицу возможные варианты значений высказываний с учётом условия задачи, что одно из утверждений верно, а два - ложны:
Слайд 53Задача 4.
Три молодые мамы Анна, Ирина, Ольга, гуляя в парке со
Анна: моего малыша зовут Денис, а Кирилл - сын Ирины.
Ирина: моего сыночка зовут Максим, а Кирилл - сын Анны.
Ольга: мой мальчик - Кирилл, а сына Анны зовут Максим.
Каждая из них один раз сказала правду и один раз солгала. Как зовут мальчиков Анны, Ирины и Ольги ? (В ответе перечислить первые буквы имен, например, КМД)
Решение:
Введём обозначения: А – Анна, И– Ирина, О – Ольга, Д – Денис, К –Кирилл, М – Максим. Тогда суждения Подруг с учетом того, что каждая сказала правду наполовину, можно записать коротко следующим образом:
Анна: А ⋅ Д + И ⋅ К = 1; Ирина: И ⋅ М + А ⋅ К = 1; Ольга: О ⋅ К + А ⋅ М = 1
Далее решаем методом рассуждений. Рассмотри высказывание Анны : А ⋅ Д + И ⋅ К = 1.
Возможны два случая:
Таким образом, делаем вывод, что
сына Анны зовут Денис, сына Ирины – Максим, а сына Ольги - Кирилл.
Ответ: ДМК.