- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Логические операции
Содержание
- 1. Презентация по информатике на тему Логические операции
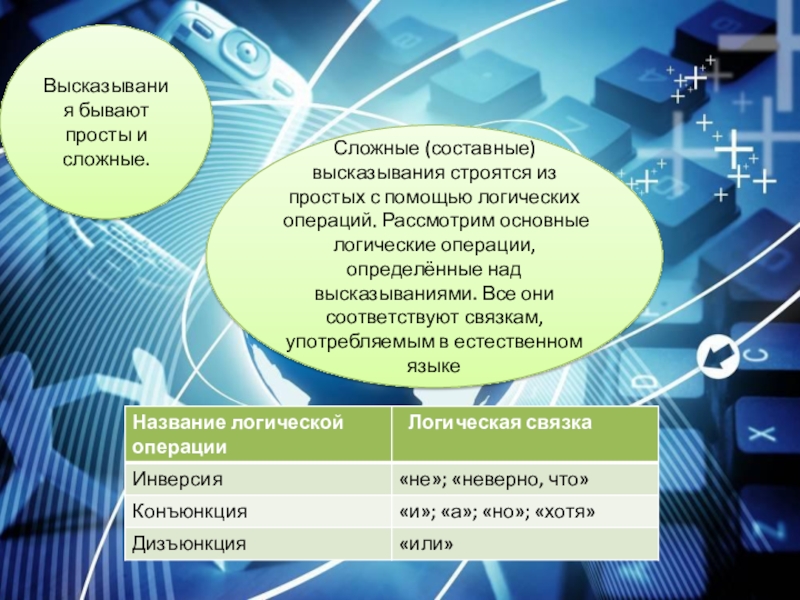
- 2. КонъюнкцияКонъюнкция — логическая операция, ставящая в соответствие
- 3. Для записи конъюнкции используются следующие знаки: И,ˆ,⋅,&.
- 4. ДизъюнкцияДизъюнкция — логическая операция, которая каждым двум
- 5. Для записи дизъюнкции используются следующие знаки: ИЛИ;∨;|;+.Например:
- 6. ИнверсияИнверсия — логическая операция, которая каждому высказыванию
- 7. Отрицанием высказывания «У меня дома есть компьютер»
- 8. Любое сложное высказывание можно записать и виде
- 9. Слайд 9
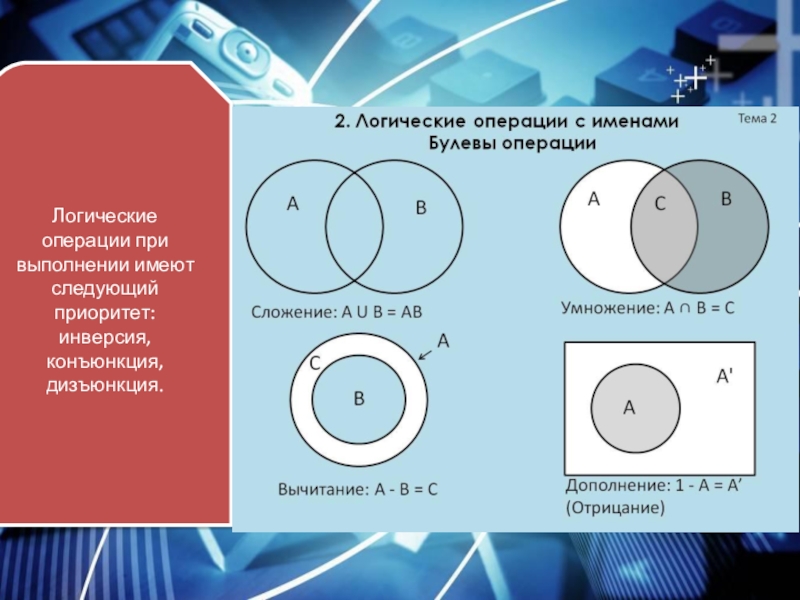
- 10. Логические операции при выполнении имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.
Слайд 1Высказывания бывают просты и сложные.
Сложные (составные) высказывания строятся из простых с
Слайд 2Конъюнкция
Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое
Рассмотрим два высказывания:
A = «Основоположником алгебры логики является Джордж Буль»,
B = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике».
Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания.
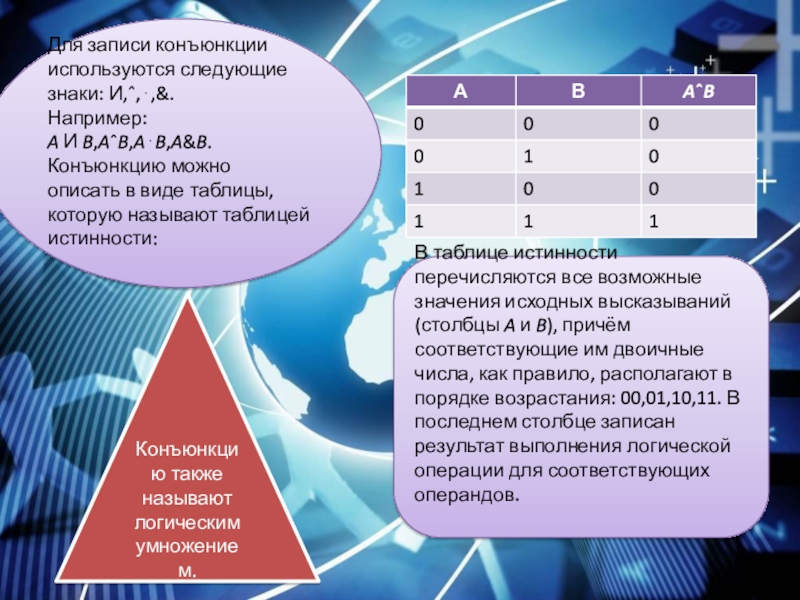
Слайд 3Для записи конъюнкции используются следующие знаки: И,ˆ,⋅,&.
Например: A И B,AˆB,A⋅B,A&B.
Конъюнкцию можно
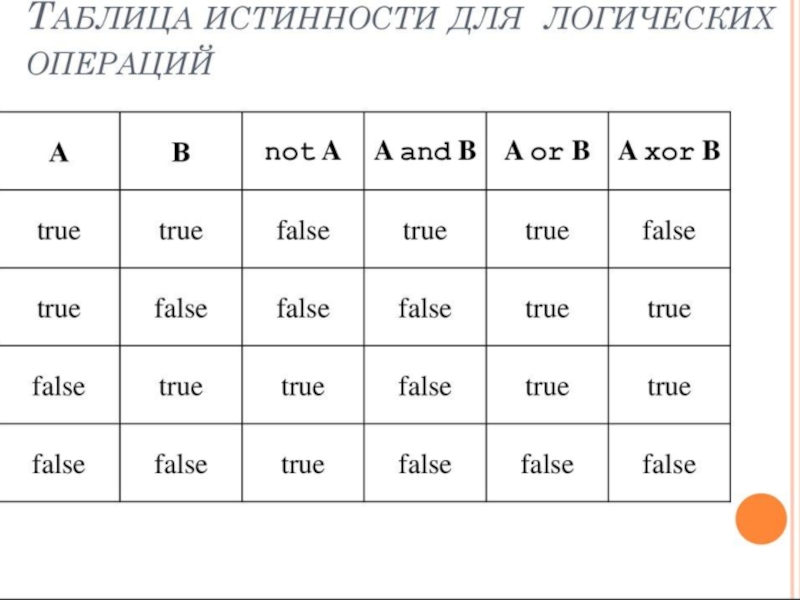
В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы A и B), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00,01,10,11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов.
Конъюнкцию также называют логическим умножением.
Слайд 4Дизъюнкция
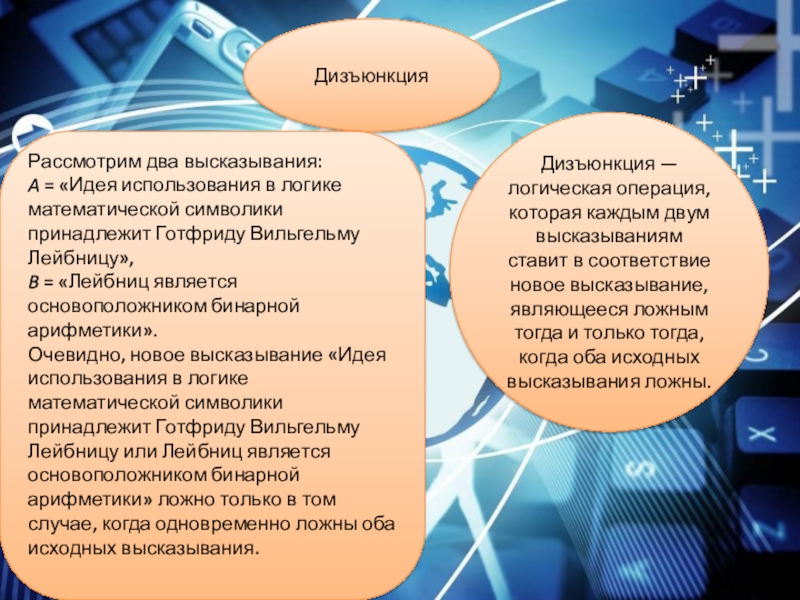
Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие
Рассмотрим два высказывания:
A = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу»,
B = «Лейбниц является основоположником бинарной арифметики».
Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.
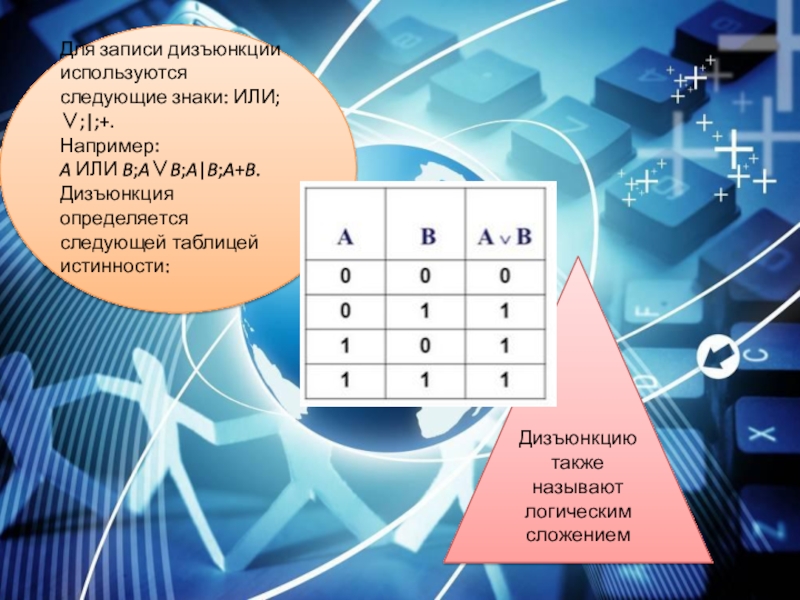
Слайд 5Для записи дизъюнкции используются следующие знаки: ИЛИ;∨;|;+.
Например: A ИЛИ B;A∨B;A|B;A+B.
Дизъюнкция определяется следующей таблицей
Дизъюнкцию также называют логическим сложением
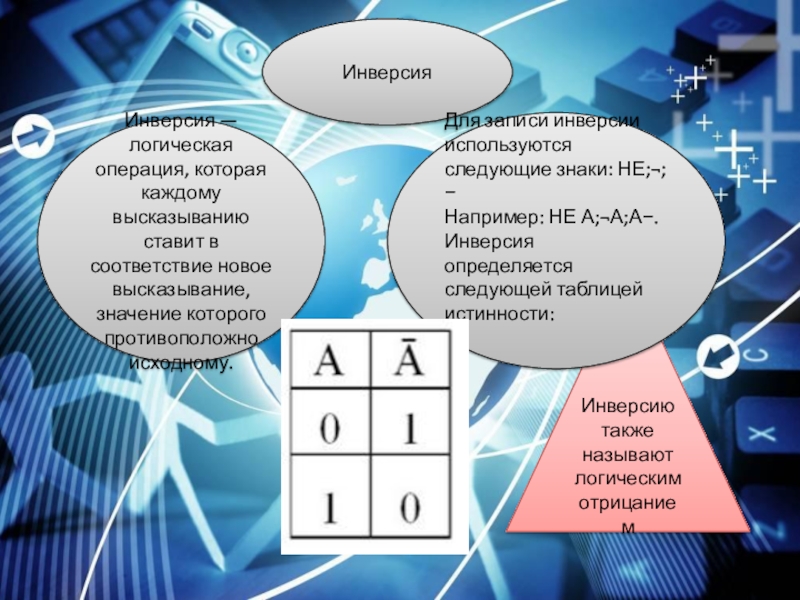
Слайд 6Инверсия
Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое
Инверсию также называют логическим отрицанием
Для записи инверсии используются следующие знаки: НЕ;¬;−
Например: НЕ А;¬А;А−.
Инверсия определяется следующей таблицей истинности:
Слайд 7Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что
Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке: «Я знаю китайский язык».
Отрицанием высказывания «Все юноши 8−х классов — отличники» является высказывание «Неверно, что все юноши 8−х классов — отличники», другими словами, «Не все юноши 8−х классов — отличники».
Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что ...», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».
Слайд 8Любое сложное высказывание можно записать и виде логического выражения — выражения,
Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция.
Изменить порядок выполнения операций можно с помощью расстановки скобок.