- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике и ИКТ на тему: Системы счисления (8 класс)
Содержание
- 1. Презентация по информатике и ИКТ на тему: Системы счисления (8 класс)
- 2. Содержание1. Основные понятия. Виды систем счисления2. Непозиционные
- 3. Основные понятияСистема счисления- это способ записи чисел
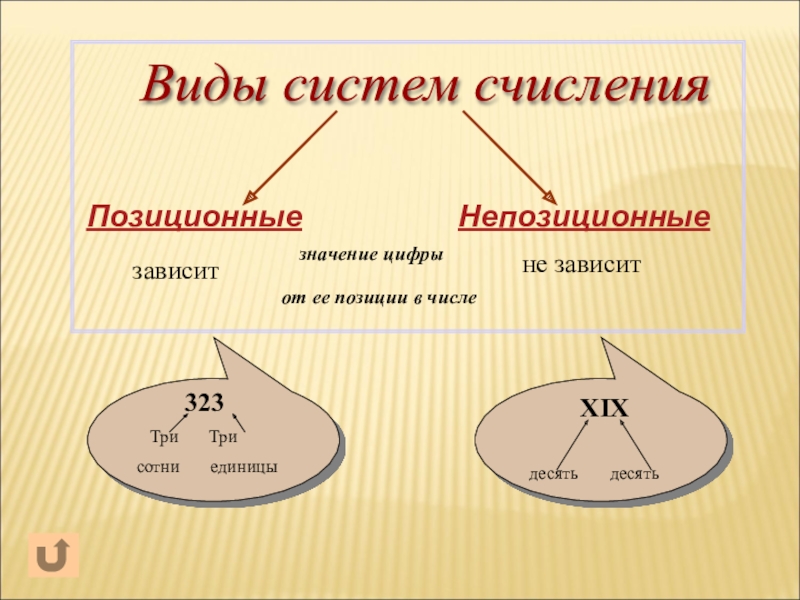
- 4. зависит не зависит
- 5. Непозиционные системы счисления
- 6. Слайд 6
- 7. = 3 4 5
- 8. = 60 +20+2 = 82
- 9. X X X I I= 32D X L I I= 542Найдите значения чисел:
- 10. Слайд 10
- 11. – основание (p)
- 12. Алфавиты систем счисленияДля записи чисел в позиционной
- 13. ПРИМЕРЫ: (перепиши, вставляя пропущенные числа)p = 10
- 14. Вопрос для обсуждения
- 15. Система счисления, применяемая в современной математике, является
- 16. Рассмотрим десятичное число 555:5 5 5 10единицыдесяткисотниИз
- 17. В развернутой форме записи числа умножение цифр
- 18. Слайд 18
- 19. Двоичная система счисления является позиционной системой счисления.Алфавит
- 20. В развернутой форме число записывается в виде
- 21. Восьмеричная система счисления является позиционной системой счисления.Алфавит
- 22. В развернутой форме число записывается в виде
- 23. Шестнадцатеричная система счисления является позиционной системой счисления.Алфавит
- 24. В развернутой форме число записывается в виде
- 25. Алгоритм перевода чисел,записанных в произвольной системе
- 26. Задания для самостоятельного выполненияЗадание 1Задание 2Задание 3Задание 4Задание 5Задание 6
- 27. Ответ: а) 341 (р=5)
- 28. Ответ: а) в троичной СС для записи
- 29. Ответ: 11112 = 1510.Какое максимальное число
- 30. Ответ: четное число в двоичной системе
- 31. Ответ: да, если считать числа в задаче,
- 32. Ответ: алфавит пятеричной системы счисления – цифры
- 33. Слайд 33
Слайд 2Содержание
1. Основные понятия. Виды систем счисления
2. Непозиционные системы счисления
3. Позиционные системы
4. Десятичная система счисления
5. Двоичная система счисления
6. Восьмеричная система счисления
7. Шестнадцатеричная система счисления
8. Перевод чисел в десятичную сс
9. Задания для самостоятельного выполнения
Слайд 3Основные понятия
Система счисления
- это способ записи чисел и правила действий над
Число
- это величина, а не символьная запись.
Цифра
- набор символов, участвующих в записи числа.
Алфавит
- совокупность различных цифр, используемых для записи числа.
Слайд 11– основание (p)
Совокупность всех цифр
– алфавит
Позиционные системы могут иметь различный алфавит (2,3,4 знака).
Позиционные системы счисления
Каждая позиционная система счисления имеет определенный алфавит и основание.
системы счисления
Слайд 12Алфавиты систем счисления
Для записи чисел в позиционной системе с основанием р
Позиция цифры в числе называется разрядом.
Слайд 13ПРИМЕРЫ: (перепиши, вставляя пропущенные числа)
p = 10 (десятичная с/c)
p = 4 (четверичная с/c)
1 2 3 10 11 12 13 20 21 22 23 30 __ __ __ __
3. p = 2 (двоичная с/c)
1 10 11 100 101 110 111 1000 ___ 1010 1011 ____ ___ ___ ___ 10000 _____ _____
4. p = 16 (шестнадцатеричная с/c)
1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B ___ ___ ___ ___
31 32 33 100
1001
1C 1D 1E 1F
Слайд 15Система счисления, применяемая в современной математике, является позиционной десятичной системой.
Её основание
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - алфавит.
Слайд 16Рассмотрим десятичное число 555:
5 5 5 10
единицы
десятки
сотни
Из двух написанных рядом одинаковых
Слайд 17В развернутой форме записи числа умножение цифр производится в явной форме:
55510
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания:
555,5510 = 5·102 + 5·101 + 5·100 + 5·10-1 + 5·10-2
2 1 0 -1 -2
Любое число в отрицательной степени = единица / число в положительной степени: 10 -1 =1/10 1 , 10-2 = 1/102
Слайд 19Двоичная система счисления является позиционной системой счисления.
Алфавит двоичной системы – две
Из двух написанных рядом одинаковых цифр левая в два раза больше правой.
Слайд 20В развернутой форме число записывается в виде суммы ряда степеней основания
Число в свернутой форме записывается так:
101,012
101,012 = 1·22 + 0·21 + 1·20 + 0·2-1 + 1·2-2
2 1 0 -1 -2
= 5,2510
Слайд 21Восьмеричная система счисления является позиционной системой счисления.
Алфавит восьмеричной системы – цифры
Из двух написанных рядом одинаковых цифр левая в восемь раз больше правой.
Слайд 22В развернутой форме число записывается в виде суммы ряда степеней основания
Число в свернутой форме записывается так:
137,28
137,28 = 1·82 + 3·81 + 7·80 + 2·8-1
Номер разряда стоящей в нем цифры равен значению степени основания
2 1 0 -1
= 95,2510
Слайд 23Шестнадцатеричная система счисления является позиционной системой счисления.
Алфавит шестнадцатеричной системы – цифры
Из двух написанных рядом одинаковых цифр левая в шестнадцать раз больше правой.
(Десятичное значение: A=10, B=11, C=12, D=13, E=14, F=15)
Слайд 24В развернутой форме число записывается в виде суммы ряда степеней основания
Число в свернутой форме записывается так:
12A,416
12A,416 = 1·162 + 2·161 + 10·160 + 4·16-1
Номер разряда стоящей в нем цифры равен значению степени основания
2 1 0 -1
= 298,2510
Слайд 25 Алгоритм перевода чисел,
записанных в произвольной системе счисления,
в десятичную систему счисления
1.
2. Вычислить полученную сумму.
231,24 = 2·42 + 3·41 + 1·40 + 2·4-1
2 1 0 -1
= 45,510
1123 =
1346 =
1·32 + 1·31 + 2·30 = 1410
1·62 + 3·61 + 4·60 = 5810
Переведи в десятичную сс:
Слайд 26Задания для самостоятельного выполнения
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Слайд 27Ответ: а) 341 (р=5) в)
б) 123 (р=4) г) 111 (р=2)
Какое минимальное основание должна иметь система счисления, если в ней можно записать числа:
а) 341
б) 123
в) 222
г) 111
Слайд 28Ответ: а) в троичной СС для записи чисел используются цифры 0
б) в девятиричной СС для записи чисел используются цифры 0 1 2 3 4 5 6 7 8, значит цифры 419 и 4А записаны неверно
Какое число ошибочно записано в:
а) троичной СС – 79, 212, 531
б) девятеричной СС – 419, 832, 4А
Слайд 29Ответ: 11112 = 1510.
Какое максимальное число можно записать в двоичной
Переведите полученное число в десятичную систему счисления.
Слайд 30Ответ: четное число в двоичной системе счисления оканчивается на 0,
а) 1012 = 510 б) 1102 = 610
в) 10012 = 910 г) 1002 = 410
Определите четное число или нечетное:
а) 1012
б) 1102
в) 10012
г) 1002
Сформулируйте критерий четности в двоичной системе счисления.
Слайд 31Ответ: да, если считать числа в задаче, представленными в двоичной системе
112= 1⋅21 + 1⋅20 = 310;
1102 = 1⋅22 + 1⋅21 + 0⋅20 = 4 + 2 = 610
Было 11 яблок. После того как каждое яблоко разрезали пополам, стало 110 половинок.
Возможно ли это? Обоснуйте ответ.
Слайд 32Ответ: алфавит пятеричной системы счисления – цифры (0,1,2,3,4).
Выпишите алфавит традиционной позиционной пятеричной системы счисления.
Переведите число 325 в десятичную систему счисления.