г. Тверь
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Алгоритмы на графах. Определение наличия циклов в графе
Содержание
- 1. Презентация по информатике Алгоритмы на графах. Определение наличия циклов в графе
- 2. Домашнее заданиеКакое максимальное количество рёбер может быть
- 3. Циклы и топологическая сортировкаЕсли в графе есть
- 4. Поиск циклов в графеИспользуем DFS для нахождения
- 5. Поиск циклов в графеРассмотрим цикл и момент,
- 6. Поиск циклов в графеКак определить сам цикл?Сделаем
- 7. Поиск циклов в графеPascalfor i := 1
- 8. Поиск циклов в графеКак запомнить все вершины,
- 9. Поиск циклов в графеВ первой строке файла
- 10. Домашнее заданиеВерно ли утверждение, что из всех
Домашнее заданиеКакое максимальное количество рёбер может быть в ориентированном ациклическом графе с n вершинами?Может ли быть так, что правильным результатом топологической сортировки графа оказывается любой порядок его вершин?Решить задачу о производстве деталей с помощью DFS.Как использовать
Слайд 2Домашнее задание
Какое максимальное количество рёбер может быть в ориентированном ациклическом графе
с n вершинами?
Может ли быть так, что правильным результатом топологической сортировки графа оказывается любой порядок его вершин?
Решить задачу о производстве деталей с помощью DFS.
Как использовать топологическую сортировку для определения наличия циклов в графе?
Может ли быть так, что правильным результатом топологической сортировки графа оказывается любой порядок его вершин?
Решить задачу о производстве деталей с помощью DFS.
Как использовать топологическую сортировку для определения наличия циклов в графе?
Слайд 3Циклы и топологическая сортировка
Если в графе есть циклы, то топологическая сортировка
невозможна.
Если граф ациклический, то можно выполнить топологическую сортировку.
Как с помощью топологической сортировки определить наличие циклов в графе?
Pascal
Cycles := False;
for i := 1 to n do
for j := 1 to n do
if A[i, j] and
(order[j] > order[i]) then
Cycles := True;
C
Cycles = FALSE;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
if(A[i, j] &&
(order[j] > order[i]))
Cycles = TRUE;
Слайд 4Поиск циклов в графе
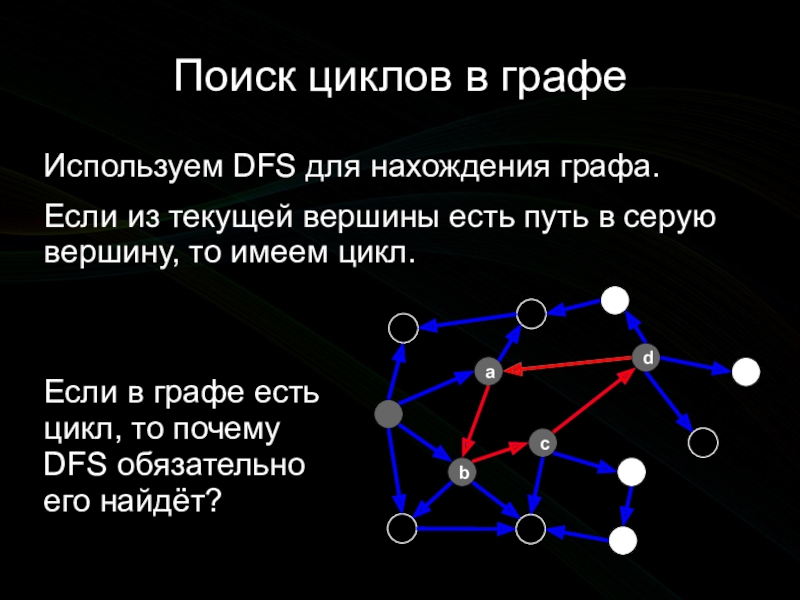
Используем DFS для нахождения графа.
Если из текущей вершины
есть путь в серую вершину, то имеем цикл.
Если в графе есть цикл, то почему DFS обязательно его найдёт?
Слайд 5Поиск циклов в графе
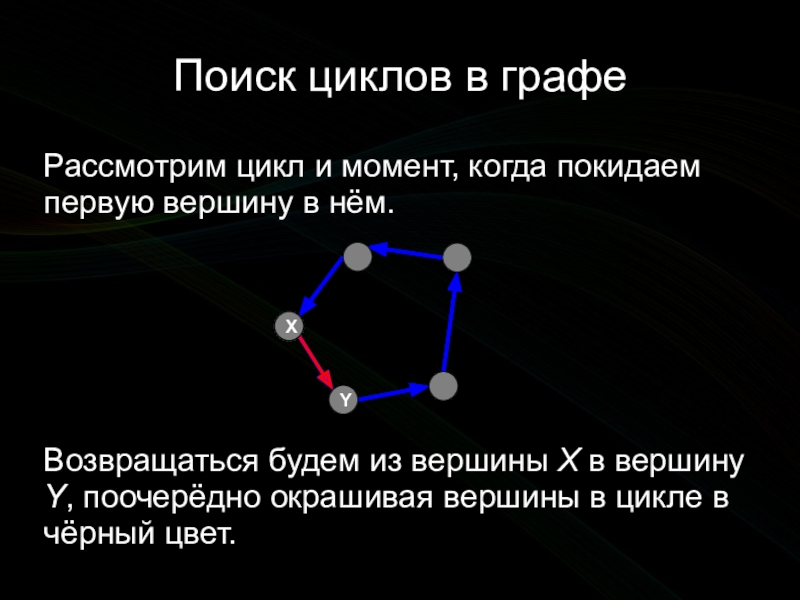
Рассмотрим цикл и момент, когда покидаем первую вершину
в нём.
Возвращаться будем из вершины X в вершину Y, поочерёдно окрашивая вершины в цикле в чёрный цвет.
Слайд 6Поиск циклов в графе
Как определить сам цикл?
Сделаем стек. При заходе в
вершину помещаем её в стек, при выходе — забираем её оттуда.
массив stack длины n — стек вершин;
sp — указатель вершины стека (число элементов в нём).
массив stack длины n — стек вершин;
sp — указатель вершины стека (число элементов в нём).
Pascal
sp := 0;
Push(v):
Inc(sp);
stack[sp] := v;
Pop:
Dec(sp);
C
sp = 0;
Push(v):
stack[++sp - 1] = v;
Pop:
sp--;
Слайд 7Поиск циклов в графе
Pascal
for i := 1 to n do
color[i]
:= WHITE;
rm := False; found := False; DFS(1);
DFS(v):
color[v] := GRAY; Push(v);
for do
if not Found then
if color[u] = WHITE then
DFS(u)
else
if color[u] = GRAY then
begin
Found := True;
cc := u; rm := True;
end;
if Found then
<запомнить текущую вершину>;
color[v] := BLACK; Pop;
rm := False; found := False; DFS(1);
DFS(v):
color[v] := GRAY; Push(v);
for do
if not Found then
if color[u] = WHITE then
DFS(u)
else
if color[u] = GRAY then
begin
Found := True;
cc := u; rm := True;
end;
if Found then
<запомнить текущую вершину>;
color[v] := BLACK; Pop;
C
for(i = 0; i < n; i++)
color[i] = WHITE;
rm = Found = FALSE; DFS(0);
DFS(v):
color[v] = GRAY; Push(v);
for()
if(!Found)
if(color[u] == WHITE)
DFS(u);
else
if(color[u] == GRAY)
{
rm = Found = TRUE;
cc = u;
};
if(Found)
<запомнить текущую вершину>;
color[v] = BLACK; Pop;
![Поиск циклов в графеPascalfor i := 1 to n do color[i] := WHITE;rm := False; found :=](/img/thumbs/ad05bb51a34f55542d3198f84430b44e-800x.jpg "Презентация по информатике Алгоритмы на графах. Определение наличия циклов в графе Поиск циклов в графеPascalfor i := 1 to n do color[i]")
Слайд 8Поиск циклов в графе
Как запомнить все вершины, из которых выходим?
Сделаем второй
стек. Если цикл найден, то помещаем во второй стек все покидаемые вершины, пока не встретим вершину cc.
массив stack2 длины n — стек вершин в прямом порядке;
sp2 — указатель вершины второго стека.
массив stack2 длины n — стек вершин в прямом порядке;
sp2 — указатель вершины второго стека.
Pascal
sp2 := 0;
<запомнить текущую вершину>:
if rm then
begin
rm := rm and (v <> cc);
Inc(sp2); stack2[sp2] := v;
end;
C
sp2 = 0;
<запомнить текущую вершину>:
if(rm)
{
rm &= v != cc;
stack[++sp - 1] = v;
};
Слайд 9Поиск циклов в графе
В первой строке файла input.txt заданы целые n
и m — соответственно число вершин и число рёбер ориентированного графа (1 ≤ n ≤ 10 000, 0 ≤ m ≤ 50 000). В следующих m строках файла заданы пары номеров вершин, соединённых рёбрами.
В файл output.txt вывести последовательность номеров вершин, соответствующих любому циклу в графе. Если граф ациклический, то вывести 0.
Ограничение по времени — 1 сек.
Ограничение по памяти — 16 Мб.
В файл output.txt вывести последовательность номеров вершин, соответствующих любому циклу в графе. Если граф ациклический, то вывести 0.
Ограничение по времени — 1 сек.
Ограничение по памяти — 16 Мб.
Слайд 10Домашнее задание
Верно ли утверждение, что из всех циклов в графе, проходящих
через начальную вершину, DFS прежде всего находит цикл минимальной длины? Привести доказательство или контрпример.
Решить задачу об определении наличия циклов в ориентированном графе проверкой рёбер: в выходной файл вывести 1, если в графе есть циклы, и 0 в противном случае.
Выполнить п. 2 для неориентированного графа.
Решить задачу об отыскании цикла в ориентированном графе с помощью DFS без использования второго стека.
Решить задачу об определении наличия циклов в ориентированном графе проверкой рёбер: в выходной файл вывести 1, если в графе есть циклы, и 0 в противном случае.
Выполнить п. 2 для неориентированного графа.
Решить задачу об отыскании цикла в ориентированном графе с помощью DFS без использования второго стека.
