- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Алгебра высказываний
Содержание
- 1. Презентация по информатике Алгебра высказываний
- 2. В алгебре высказываний, как и в обычной
- 3. Истинному высказыванию ставится в соответствие 1, ложному
- 4. Операция И (логическое умножение, конъюнкция)10 AB, A∧B,
- 5. Операция ИЛИ (логическое сложение, дизъюнкция)10 A ∨
- 6. Обозначение высказыванийA – Сейчас идет дождь.B –
- 7. Операция НЕ (инверсия)Если высказывание A истинно, то
- 8. Задание1. Даны два высказывания. А: {2*2=4} B:
- 9. Задание 2. Постройте отрицания следующих высказываний: 1) Число
Слайд 2
В алгебре высказываний, как и в обычной алгебре, вводится ряд операций.
Слайд 3Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом,
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А = {Аристотель - основоположник логики}.
В = {На яблонях растут бананы}.
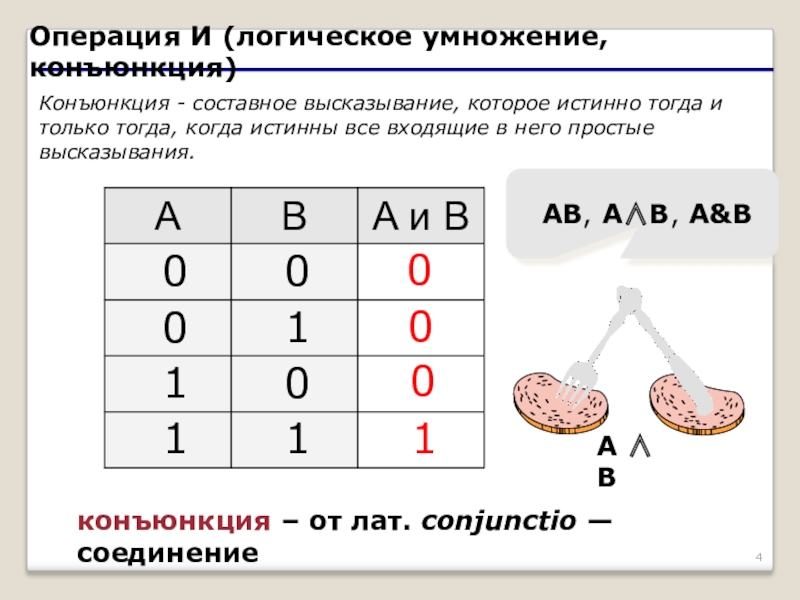
Слайд 4Операция И (логическое умножение, конъюнкция)
1
0
AB, A∧B, A&B
0
0
конъюнкция – от
A ∧ B
Конъюнкция - составное высказывание, которое истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
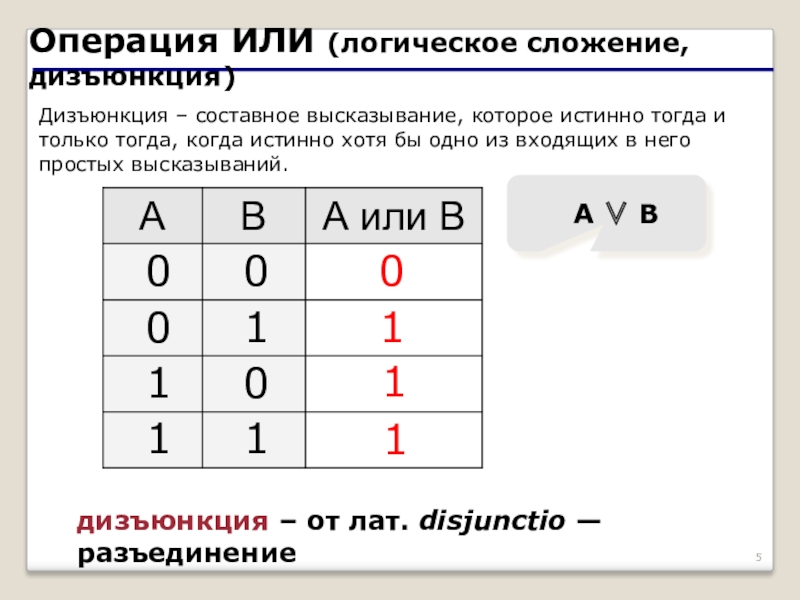
Слайд 5Операция ИЛИ (логическое сложение, дизъюнкция)
1
0
A ∨ B
1
1
дизъюнкция – от лат.
Дизъюнкция – составное высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Слайд 6Обозначение высказываний
A – Сейчас идет дождь.
B – Форточка открыта.
простые высказывания (элементарные)
Составные
A и B
A или не B
если A, то B
не A и B
A тогда и только
тогда, когда B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
Если сейчас идет дождь, то форточка открыта.
Сейчас нет дождя и форточка открыта.
Дождь идет тогда и только тогда, когда открыта форточка.
Слайд 7Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
1
0
0
1
таблица истинности операции НЕ
Логическое отрицание - ИНВЕРСИЯ – делает истинное высказывание ложным и наоборот.
Слайд 8Задание1.
Даны два высказывания. А: {2*2=4} B: {3*3=5}. Установить истинность составных
1)
2)
3) А & B
4) A V B
Слайд 9Задание 2. Постройте отрицания следующих высказываний:
1) Число 1 есть составное число.
2)
3) Неверно, что число 3 не является делителем числа 198.
4) Неверно, что любое число, оканчивающееся цифрой 4, делится на 4.
5) Некоторые млекопитающие не живут на суше.
Задание 3. Записать составное высказывание (2*2=4 и 3*3=9) или (2*2≠4 и 3*3≠9) в форме логического выражения. Построить таблицу истинности.