- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Основы алгебры логики
Содержание
- 1. Презентация Основы алгебры логики
- 2. Формы мышления Логика — наука, изучающая законы
- 3. Алгебра логики (высказываний) Алгебра в широком смысле
- 4. Задания 1, 21. Объясните, почему следующие предложения
- 5. Основные операции алгебры логики Логическое умножение (конъюнкция)в
- 6. Логическое сложение (дизъюнкция) в естественном языке
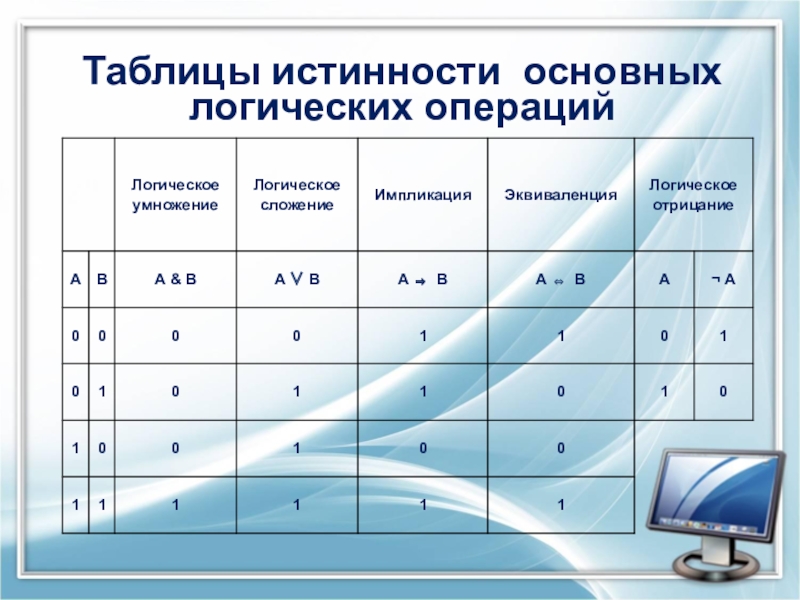
- 7. Таблицы истинности основных логических операций
- 8. Задания 3-53. Среди следующих высказываний укажите составные;
- 9. 6. Определите истинность простых высказываний: А =
- 10. Логические выражения и таблицы истинности
- 11. Задания 8, 98. Построить таблицы истинности для
- 12. Логические основы компьютераДискретный преобразователь, который выдаёт после
- 13. Логические основы компьютера Задания 10, 1110.
- 14. Ответы к заданиям 8, 98. Построить таблицы
- 15. Ответы к заданиям 10, 1110. 11. F1
Слайд 2Формы мышления
Логика — наука, изучающая законы и формы мышления.
Законы мира,
Основными формами абстрактного мышления являются понятия, высказывания (суждения) и умозаключения.
Понятие — форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов. Понятия в языке выражаются словами.
Высказывание — это форма мышления, в которой что-либо утверждается или отрицается о предметах, признаках или их отношениях.
Умозаключение — форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, мы по определенным правилам вывода получаем суждение-заключение.
Слайд 3Алгебра логики (высказываний)
Алгебра в широком смысле этого слова наука об
Высказывание — это любое предложение какого-либо языка (утверждение), содержание которого можно определить как истинное или ложное.
Всякое высказывание или истинно, или ложно; быть одновременно и тем и другим оно не может.
Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием. Высказывание, состоящее из простых высказываний, называются составным (сложным).
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А = {Аристотель - основоположник логики}
В = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0.
Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание.
Слайд 4Задания 1, 2
1. Объясните, почему следующие предложения не являются высказываниями:
1)
2) Число Х не превосходит единицы.
3) 4Х+3
4) Посмотрите в окно.
5) Пейте томатный сок!
6) Вы были в театре?
7) Сумма числа 5 и Х равна 10.
2. Какие из следующих предложений являются истинными, а какие ложными высказываниями?
Город Париж — столица Франции.
Число 2 является делителем числа 7.
3 + 5 = 2 * 4.
2 + 6 > 10.
Сканер — это устройство, которое может напечатать на бумаге то, что изображено на экране компьютера.
II + VI > VIII.
Сумма чисел 2 и 6 больше числа 8.
Мышь — устройство ввода информации.
Слайд 5Основные операции алгебры логики
Логическое умножение (конъюнкция)
в естественном языке соответствует союзу
обозначение: &;
в языках программирования обозначение: and;
иное название: логическое умножение.
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
F = A & B
Значения логической функции можно определить с помощью таблицы истинности данной функции, которая показывает, какие значения принимает логическая функции при всех возможных наборах ее аргументов.
Таблица истинности логического умножения
Слайд 6Логическое сложение (дизъюнкция)
в естественном языке соответствует союзу или;
обозначение: Ú
в языках программирования обозначение: or;
иное название: логическое сложение.
Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
Таблица истинности логического сложения
Основные операции алгебры логики
Слайд 8Задания 3-5
3. Среди следующих высказываний укажите составные; выделите в них простые,
1) Число 376 четное и трехзначное.
2) Неверно, что Солнце движется вокруг Земли.
3) Земля имеет форму шара.
4) На уроке математики старшеклассники отвечали на вопросы учителя и писали самостоятельную работу.
5) Если сумма цифр числа делится на 3, то число делится на 3.
6) Число 15 делится на 3 тогда и только тогда, когда сумма цифр числа 15 делится на 3.
4. Найдите значения логических выражений:
а) (1 Ú 1) Ú (1 Ú 0);
б) ((1 Ú 0) Ú 1) Ú 1;
в) (0 Ú 1) Ú (1 Ú 0);
г) (0&1)&1;
5. При каких значениях числа X логическое выражение не ((X > 8) или (X < -3)) примет значение:
а) ложь;
б) истина.
Слайд 9
6. Определите истинность простых высказываний:
А = {Принтер – устройство ввода
В = {Процессор – устройство обработки информации},
С = {Монитор – устройство хранения информации},
D = {Клавиатура – устройство ввода информации}.
7. Определите истинность составных высказываний:
а) (А &В) & (C Ú D); б) (А &В) Þ (C Ú D);
в) (А Ú В) Û (C & D); г) А Û В .
Задания 6,7
Слайд 10Логические выражения и таблицы истинности
Логические операции
Алгоритм построения таблицы истинности:
1. Подсчитать количество переменных n в логическом выражении.
2. Определить число строк в таблице m = 2n.
3. Подсчитать количество логических операций в формуле.
4. Установить последовательность выполнения логических операций с учетом скобок и приоритетов.
5. Определить количество столбцов в таблице: число переменных плюс число операций.
6. Выписать наборы входных переменных.
7. Провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с
установленной последовательностью.
Слайд 11Задания 8, 9
8. Построить таблицы истинности для следующих высказываний:
a)
b) A & ( А Ú B Ú C)
c) A & ( B Ú B & C)
d) (A Þ B) Û (А & В)
9. Докажите с помощью таблиц истинности равносильность следующих высказываний:
a) (А Þ В) & (А Ú B ) и b) (А Û В) & (А & В) Ú ( А & B )
Ответы
Слайд 12Логические основы компьютера
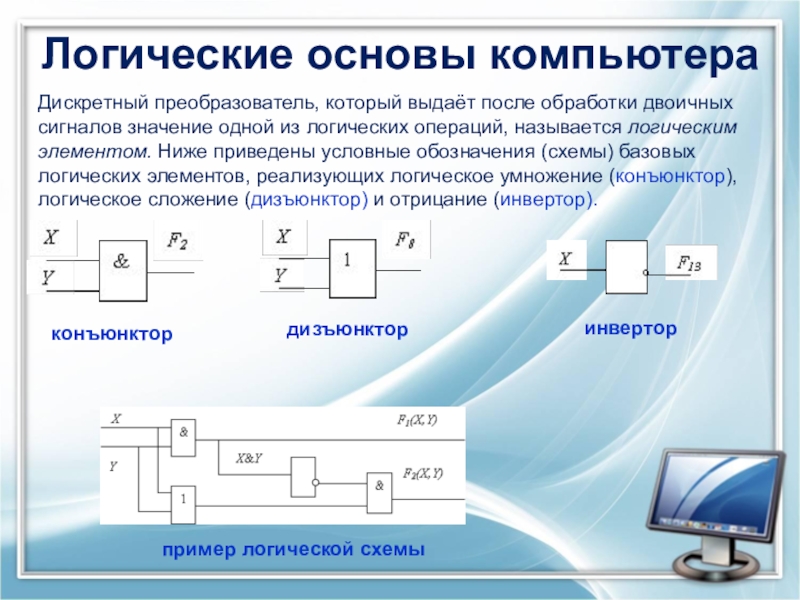
Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение
конъюнктор
дизъюнктор
инвертор
пример логической схемы
Слайд 13Логические основы компьютера
Задания 10, 11
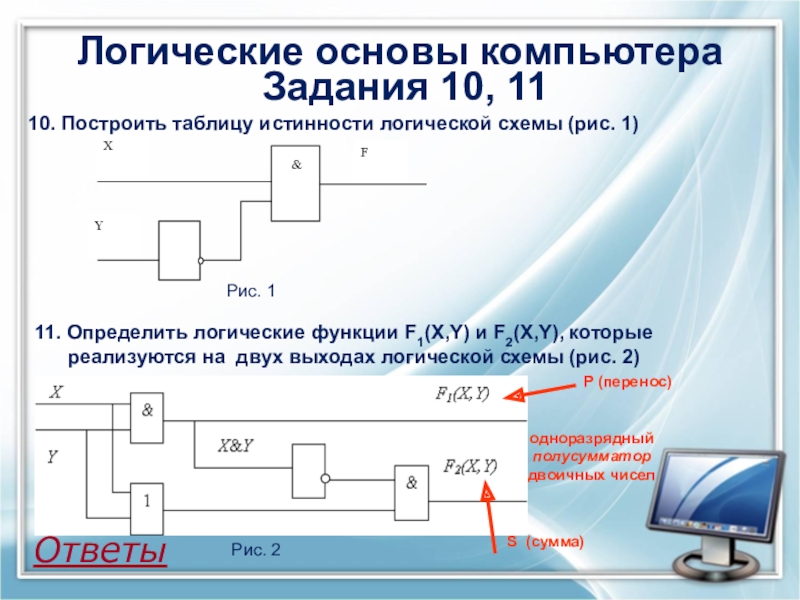
10. Построить таблицу истинности логической схемы
Рис. 1
11. Определить логические функции F1(X,Y) и F2(X,Y), которые
реализуются на двух выходах логической схемы (рис. 2)
Рис. 2
одноразрядный полусумматор двоичных чисел
P (перенос)
S (сумма)
Ответы
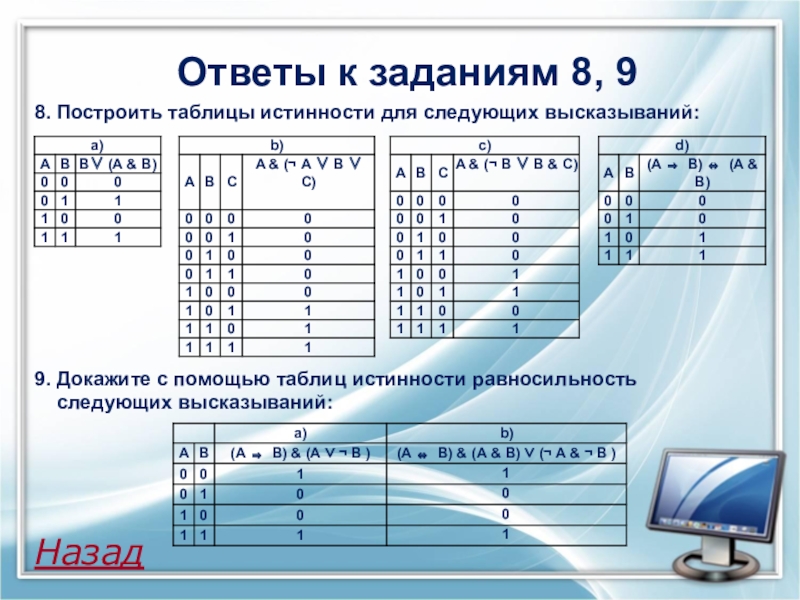
Слайд 14Ответы к заданиям 8, 9
8. Построить таблицы истинности для следующих высказываний:
9. Докажите с помощью таблиц истинности равносильность следующих высказываний:
Назад