- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Моделирование на графах 9 кл
Содержание
- 1. Презентация Моделирование на графах 9 кл
- 2. Граф Граф – это некоторое конечное множество точек, называемых
- 3. Основные понятия графаНаправленная линия (со стрелкой) называется
- 4. Немного истории Первая работа по теории графов была
- 5. Задача К XVIII веку через реку, на которой
- 6. Слайд 6
- 7. Слайд 7
- 8. Виды графов
- 9. 1. Неориентированный граф Пример: Пятеро друзей пишут письма
- 10. Задача 1 Аркадий, Борис, Владимир, Григорий и Дмитрий
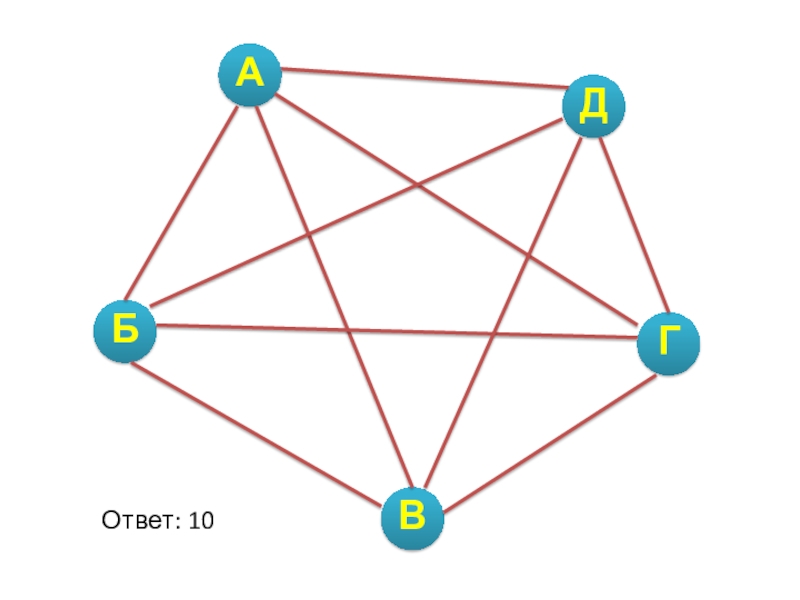
- 11. Ответ: 10
- 12. 2. Ориентированный граф Ориентированный граф - граф, вершины
- 13. 3. Взвешенный граф Взвешенный граф – это граф,
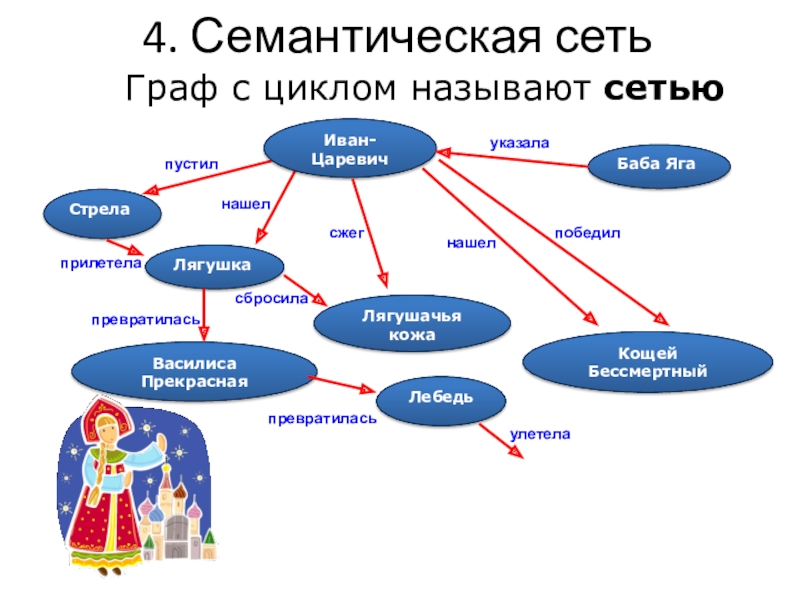
- 14. 4. Семантическая сеть Граф с циклом называют сетью
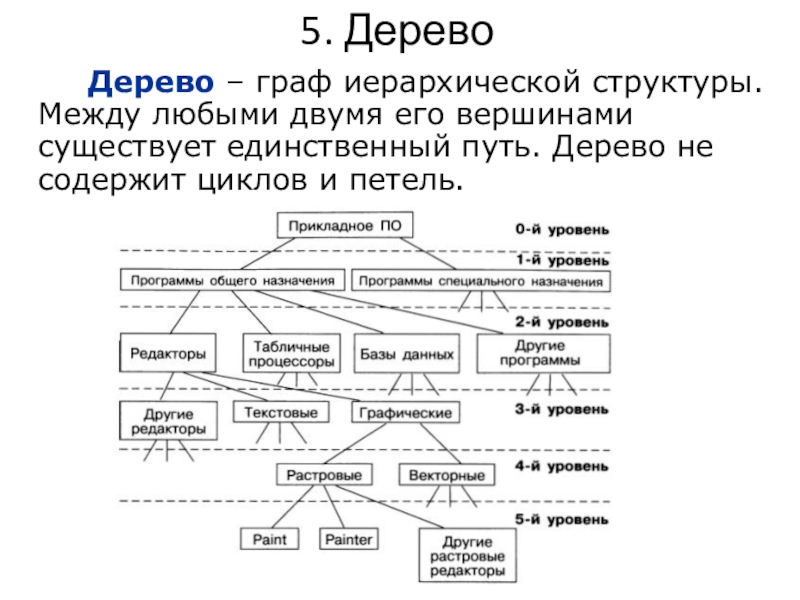
- 15. 5. Дерево Дерево – граф иерархической структуры. Между
- 16. Укажите корневую вершину, объекты 1-го, 2-го и 3-го уровней
- 17. Решение задач с помощью графов
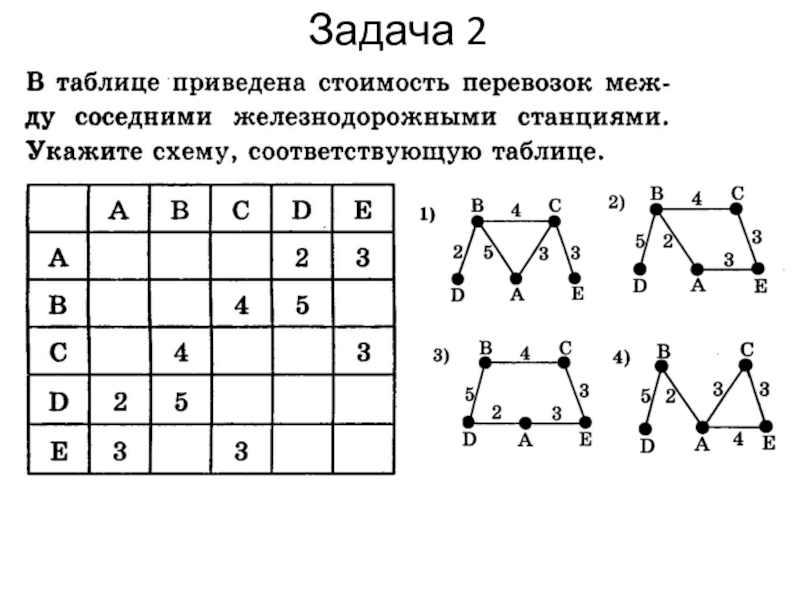
- 18. Задача 2
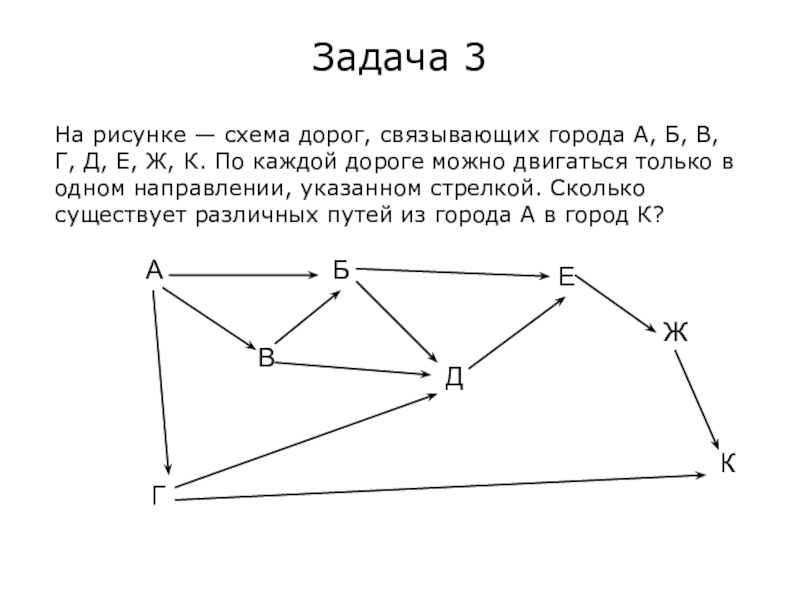
- 19. Задача 3На рисунке — схема дорог, связывающих
- 20. Задача 3 (решение)АВГБДЕЖК2 - КБДЕЖКДККЕЖЕЖКАБВГДЕЖКОтвет: 7
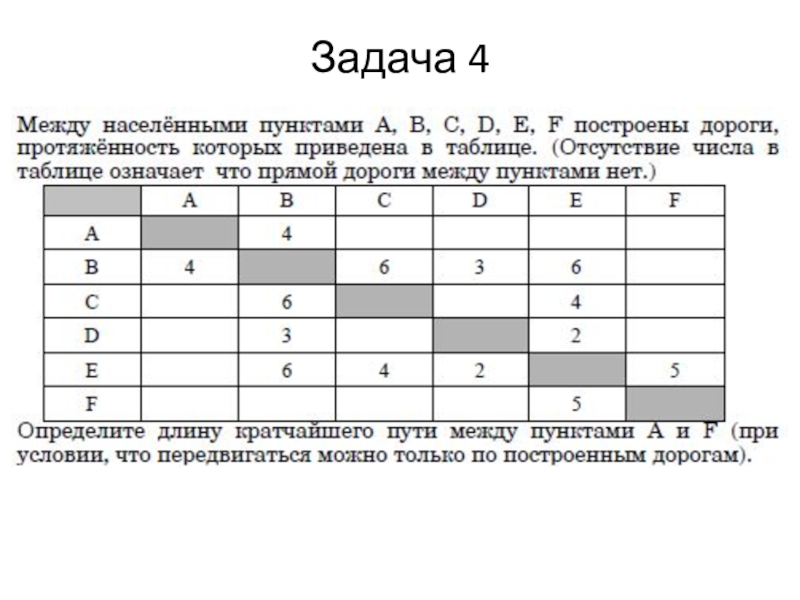
- 21. Задача 4
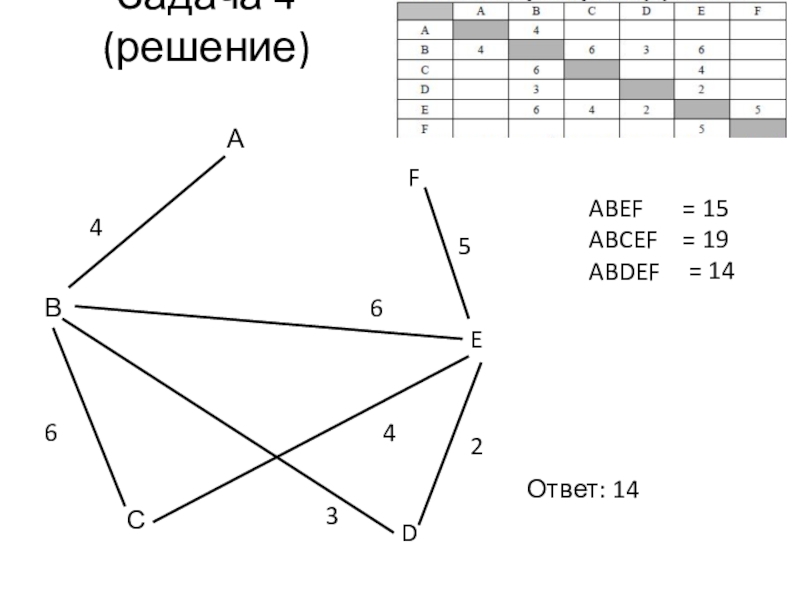
- 22. Задача 4 (решение)ВАСDEF5246364ABEFABCEFABDEF= 15= 19= 14Ответ: 14
- 23. Задача № 5 Для составления цепочек используются бусины,
- 24. Задача 5 (решение) Для составления цепочек используются бусины,
- 25. Проверь себя
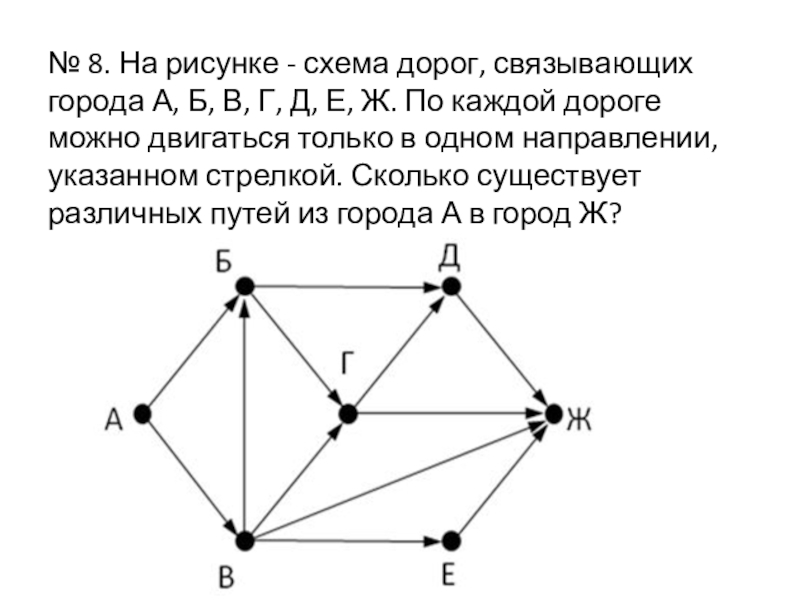
- 26. № 8. На рисунке - схема дорог,
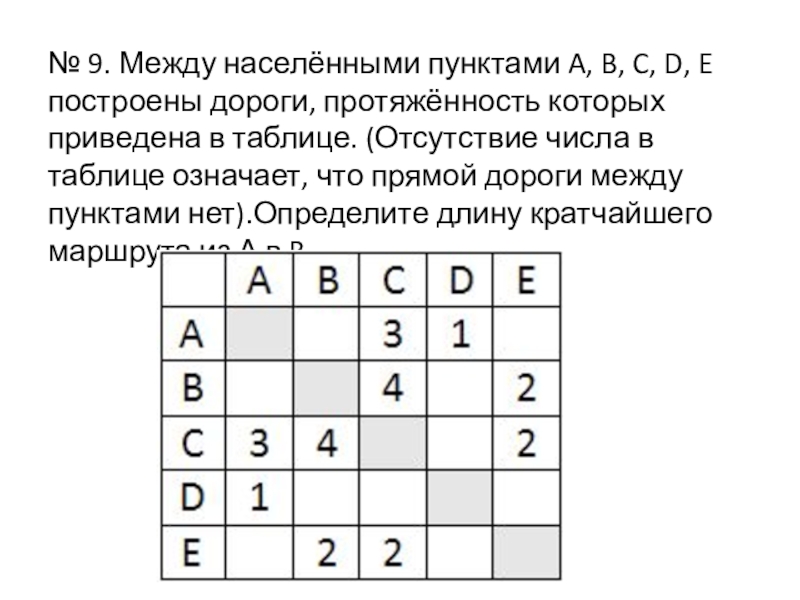
- 27. № 9. Между населёнными пунктами A, B,
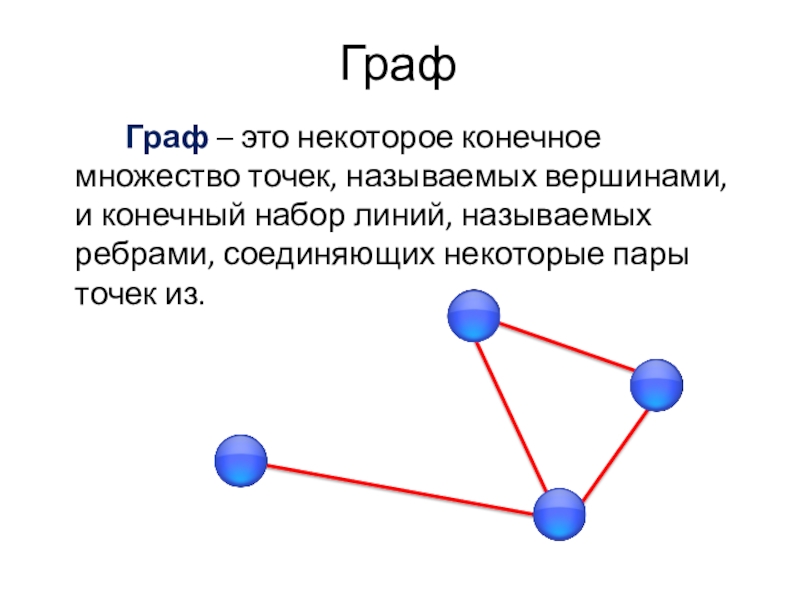
Граф Граф – это некоторое конечное множество точек, называемых вершинами, и конечный набор линий, называемых ребрами, соединяющих некоторые пары точек из.
Слайд 2Граф
Граф – это некоторое конечное множество точек, называемых вершинами, и конечный набор
линий, называемых ребрами, соединяющих некоторые пары точек из.
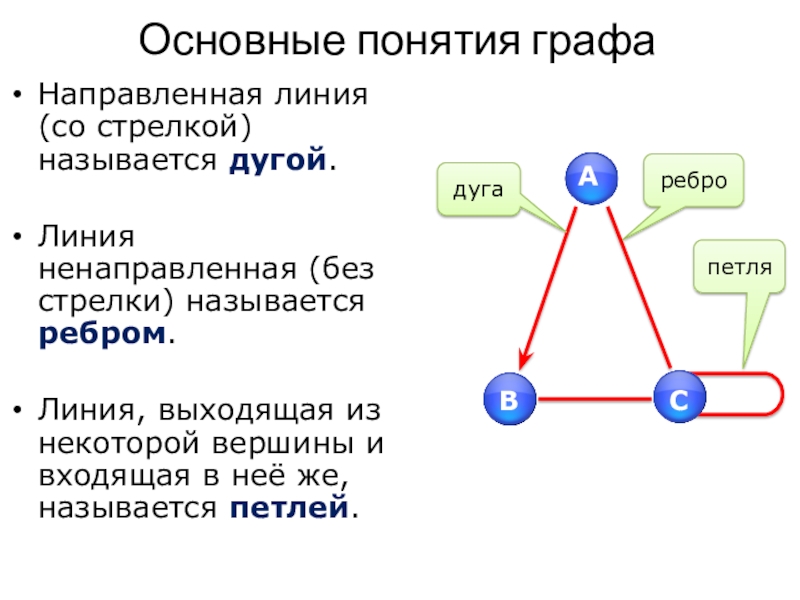
Слайд 3Основные понятия графа
Направленная линия (со стрелкой) называется дугой.
Линия ненаправленная (без стрелки)
называется ребром.
Линия, выходящая из некоторой вершины и входящая в неё же, называется петлей.
Линия, выходящая из некоторой вершины и входящая в неё же, называется петлей.
Слайд 4Немного истории
Первая работа по теории графов была написана еще в 1736
году Леонардом Эйлером. (>>>)
Впервые понятие «граф» ввел в 1936 году венгерский математик Денеш Кёниг.
Впервые понятие «граф» ввел в 1936 году венгерский математик Денеш Кёниг.
Слайд 5Задача
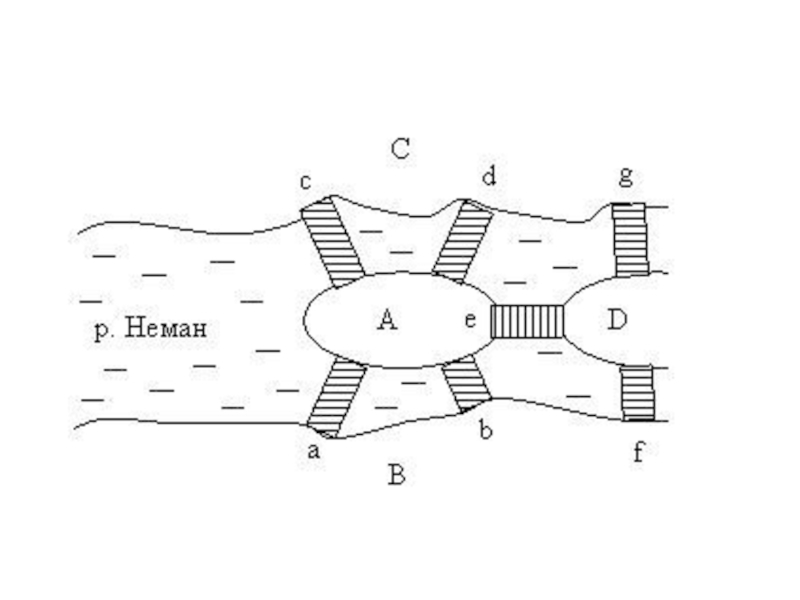
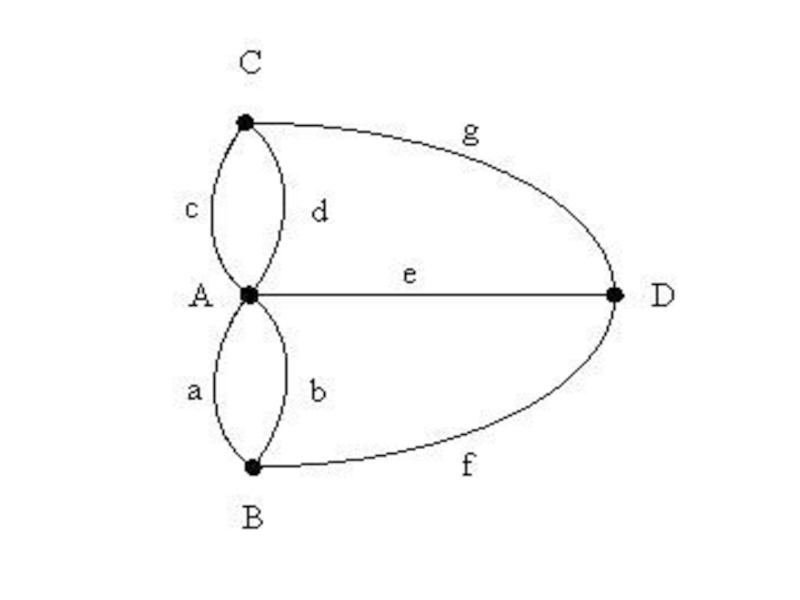
К XVIII веку через реку, на которой стоял город Кенигсберг (ныне
Калининград), было построено 7 мостов, которые связывали с берегами и друг с другом два острова, расположенные в пределах города
Задача заключается в следующем: нужно пройти (если это возможно) по всем семи мостам так, чтобы на каждом из них побывать лишь по одному разу и вернуться к тому месту, откуда начал маршрут. (>>>)
Задача заключается в следующем: нужно пройти (если это возможно) по всем семи мостам так, чтобы на каждом из них побывать лишь по одному разу и вернуться к тому месту, откуда начал маршрут. (>>>)
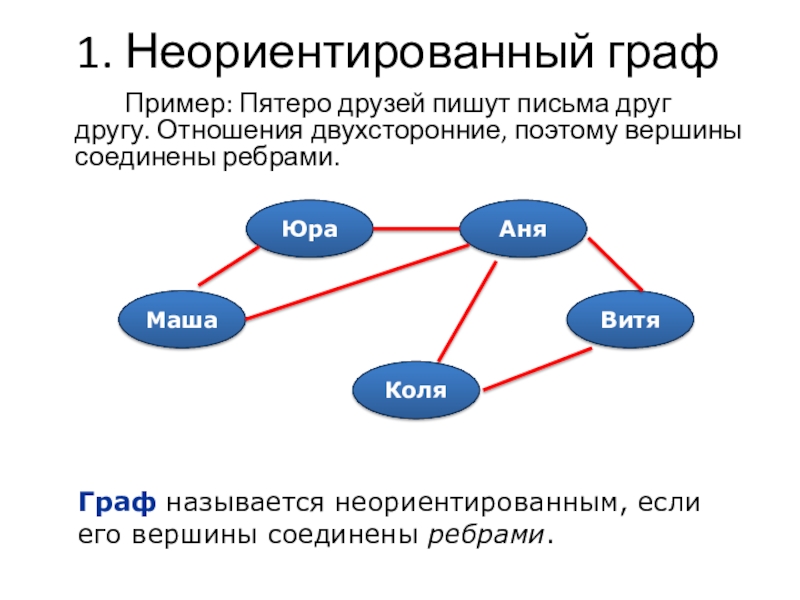
Слайд 91. Неориентированный граф
Пример: Пятеро друзей пишут письма друг другу. Отношения двухсторонние,
поэтому вершины соединены ребрами.
Граф называется неориентированным, если его вершины соединены ребрами.
Слайд 10Задача 1
Аркадий, Борис, Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями
(каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
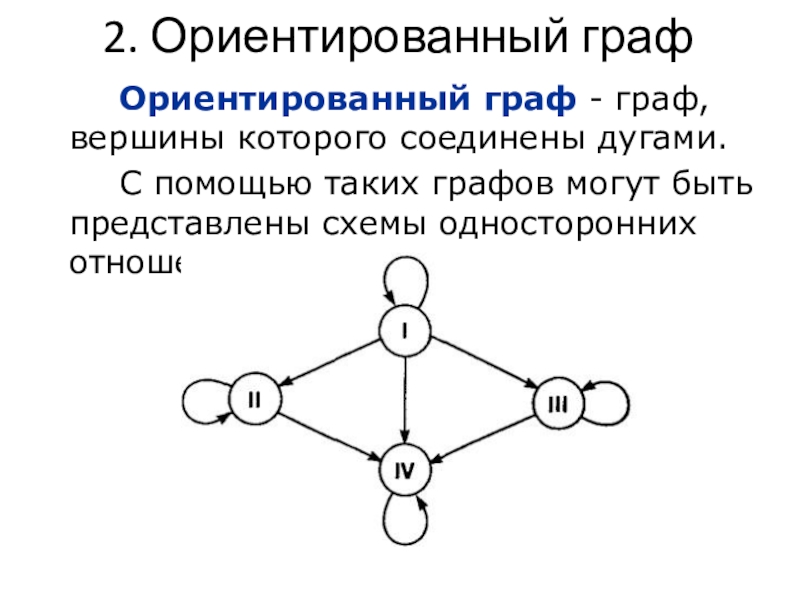
Слайд 122. Ориентированный граф
Ориентированный граф - граф, вершины которого соединены дугами.
С
помощью таких графов могут быть представлены схемы односторонних отношений.
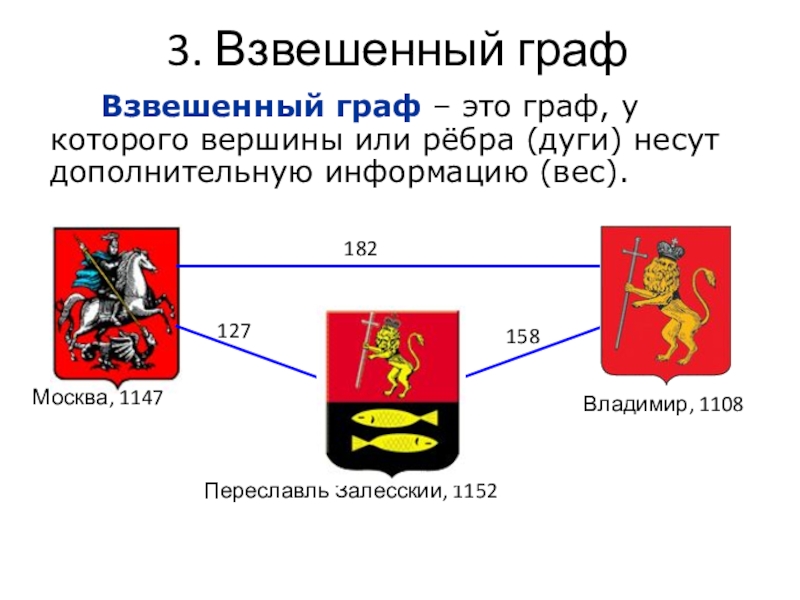
Слайд 133. Взвешенный граф
Взвешенный граф – это граф, у которого вершины или
рёбра (дуги) несут дополнительную информацию (вес).
Слайд 155. Дерево
Дерево – граф иерархической структуры. Между любыми двумя его вершинами
существует единственный путь. Дерево не содержит циклов и петель.
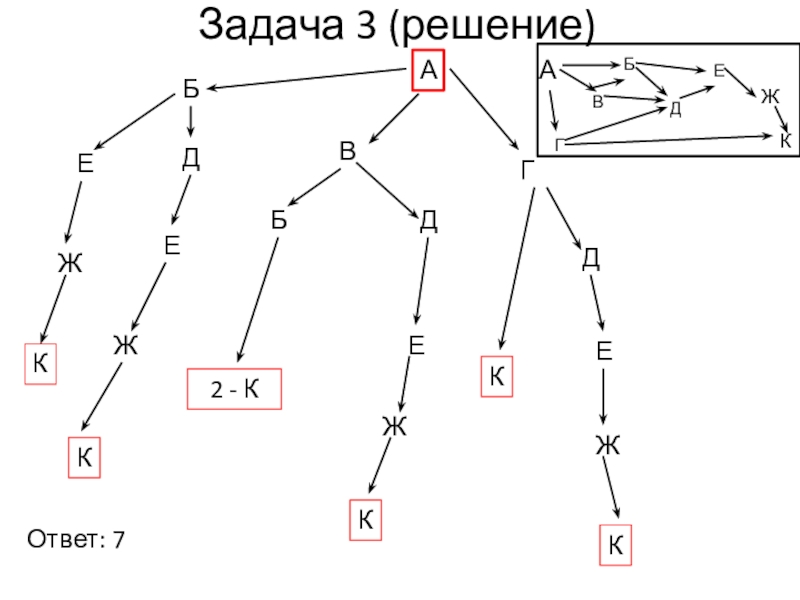
Слайд 19Задача 3
На рисунке — схема дорог, связывающих города А, Б, В,
Г, Д, Е, Ж, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Слайд 23Задача № 5
Для составления цепочек используются бусины, помеченные буквами: А, В,
С, D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая гласная, если первая буква согласная, и любая согласная, если первая гласная. На третьем месте - одна из бусин С, D, Е, не стоящая в цепочке на первом месте. Сколько цепочек можно создать по этому правилу?
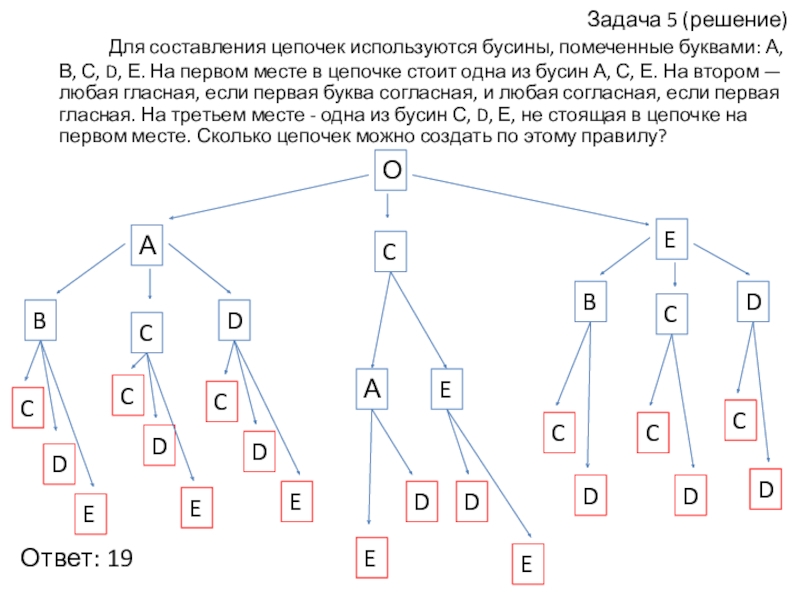
Слайд 24Задача 5 (решение)
Для составления цепочек используются бусины, помеченные буквами: А, В,
С, D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая гласная, если первая буква согласная, и любая согласная, если первая гласная. На третьем месте - одна из бусин С, D, Е, не стоящая в цепочке на первом месте. Сколько цепочек можно создать по этому правилу?
О
А
C
E
B
C
D
C
C
C
D
D
D
E
E
E
А
E
D
D
E
E
B
C
C
C
D
C
D
D
D
Ответ: 19
Слайд 26№ 8. На рисунке - схема дорог, связывающих города А, Б,
В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Слайд 27№ 9. Между населёнными пунктами A, B, C, D, E построены
дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет).Определите длину кратчайшего маршрута из А в B.