- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Кодирование и декодирование информации задание 5, ЕГЭ
Содержание
- 1. Презентация Кодирование и декодирование информации задание 5, ЕГЭ
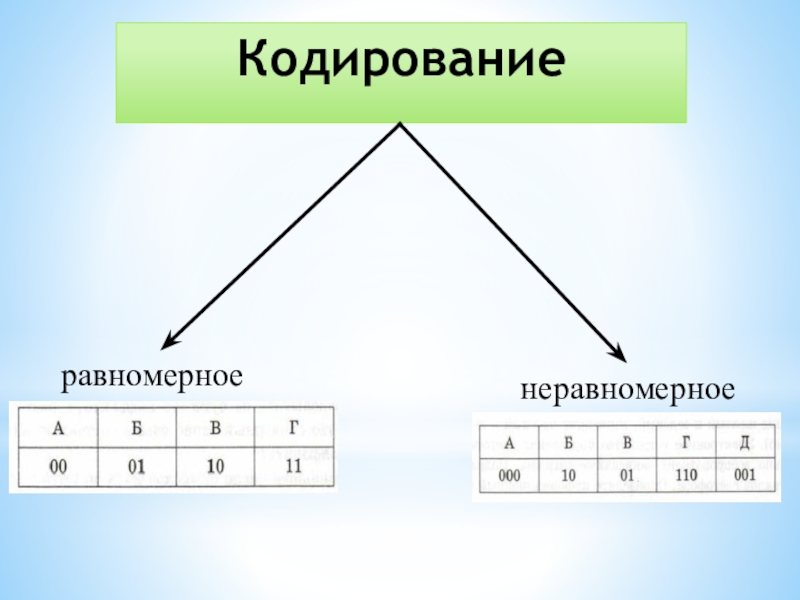
- 2. Кодированиеравномерноенеравномерное
- 3. Закодированное сообщение можно однозначно декодировать с начала,
- 4. Закодированное сообщение можно однозначно декодировать с конца,
- 5. Пример 1Пусть для кодирования первых 5 букв русского алфавита используется таблица:Раскодируйте сообщение:1100000100110
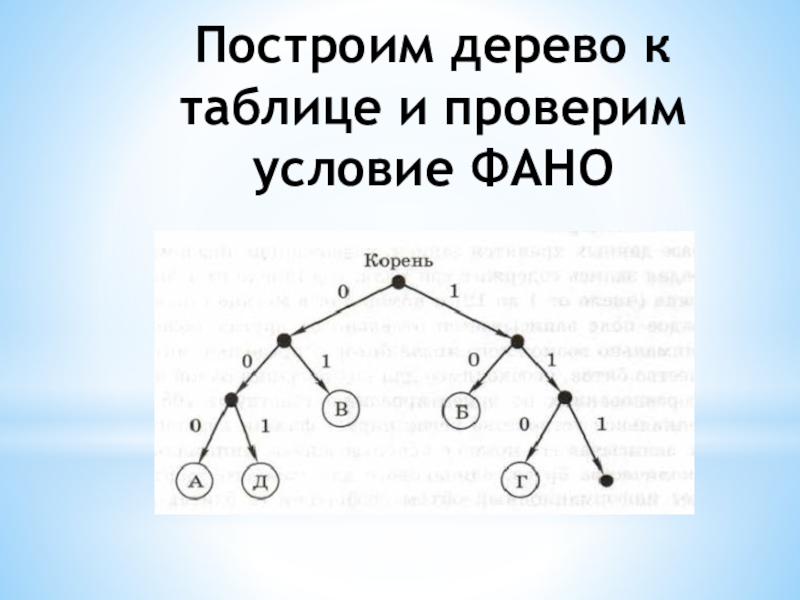
- 6. Построим дерево к таблице и проверим условие ФАНО
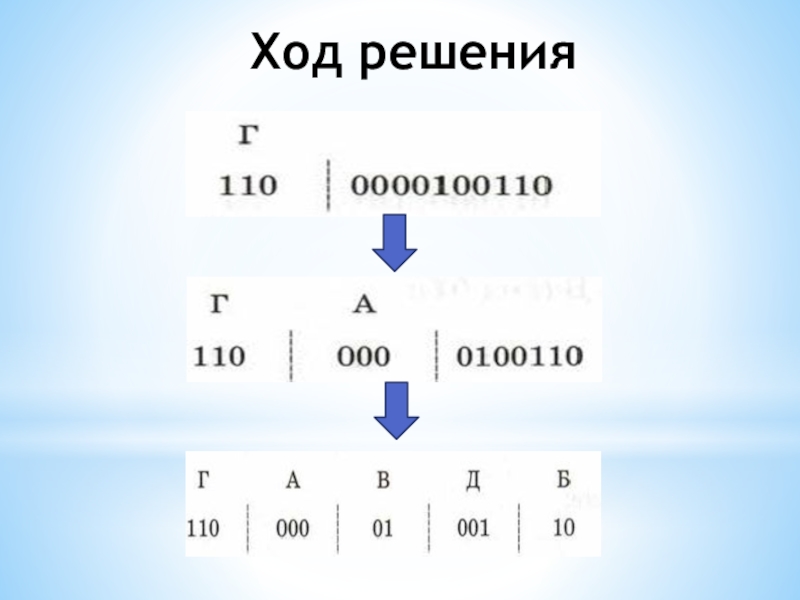
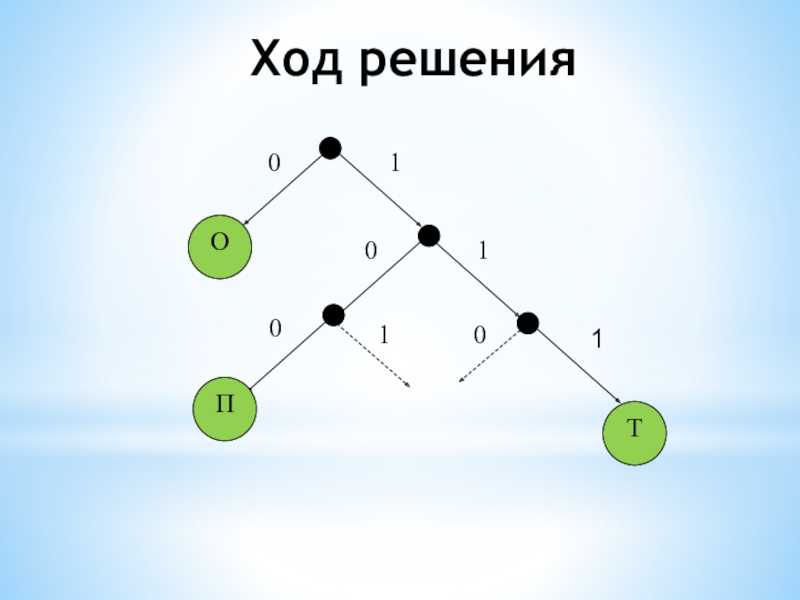
- 7. Ход решения
- 8. Пример 2Пусть для кодирования первых 5 букв русского алфавита используется таблица:
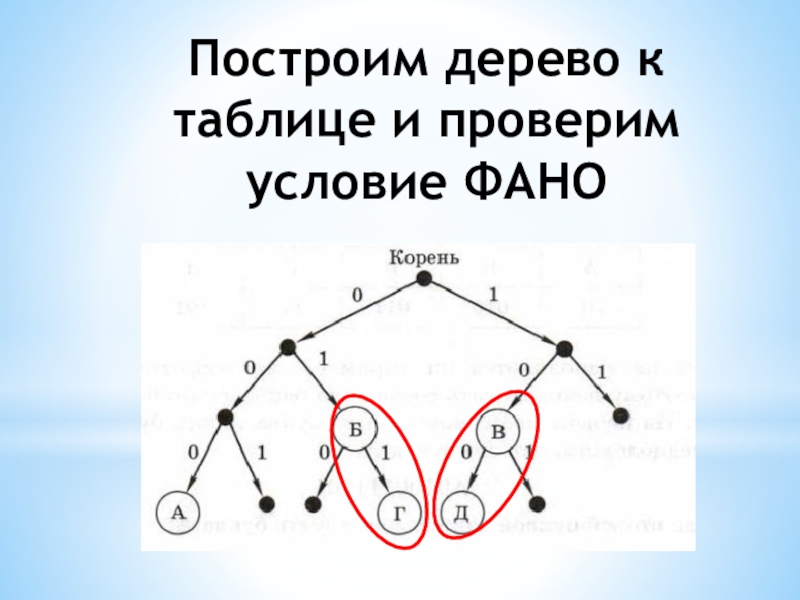
- 9. Построим дерево к таблице и проверим условие ФАНО
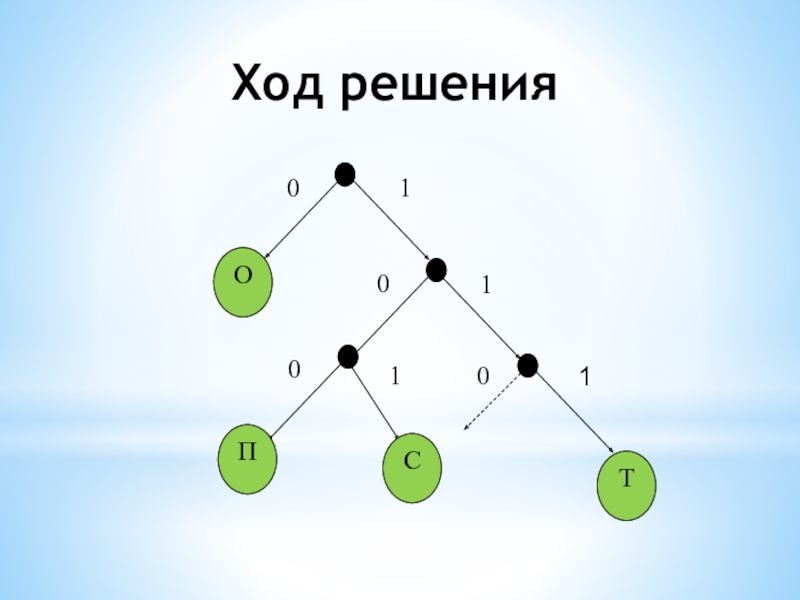
- 10. Ход решения
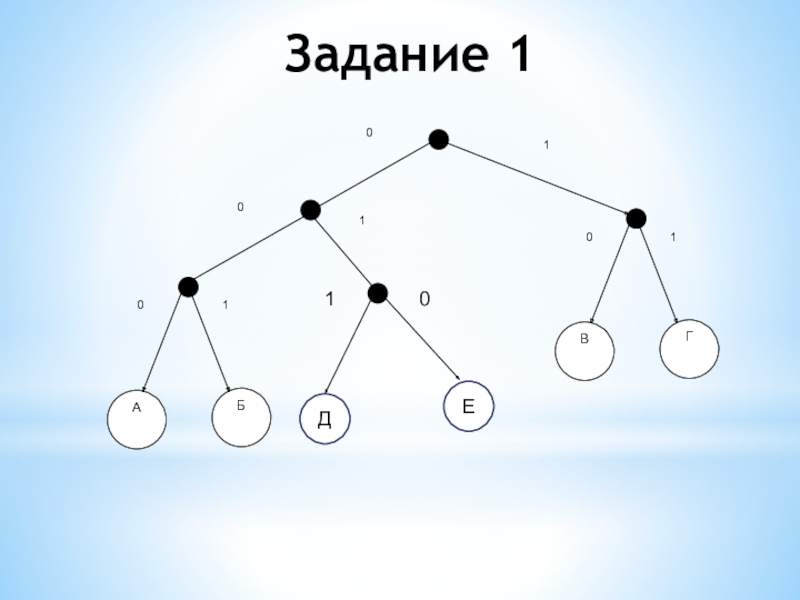
- 11. Задание 1Для кодирования некоторой последовательности, состоящей из
- 12. Задание 1ДЕ10
- 13. Задание 2По каналу связи с помощью равномерного
- 14. Расстояние Хэмминга — это количество различающихся позиций для строк с одинаковой длинной.
- 15. РешениеНайдем количество позиций, в которых отличается это
- 16. РешениеX: 01111 Y: 00001 Z: 11000W:
- 17. Задание 3Для кодирования некоторой последовательности, состоящей из
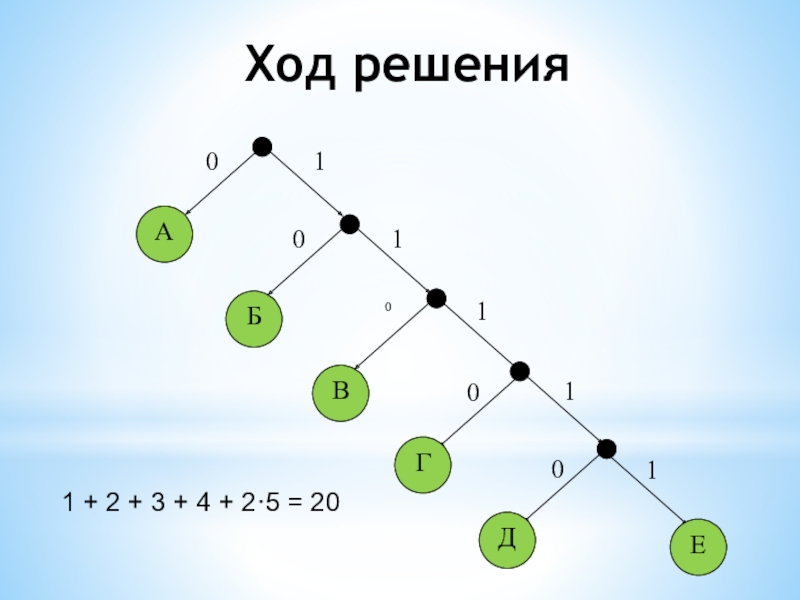
- 18. Ход решения
- 19. Ход решения1 + 2 + 3 + 4 + 2·5 = 20
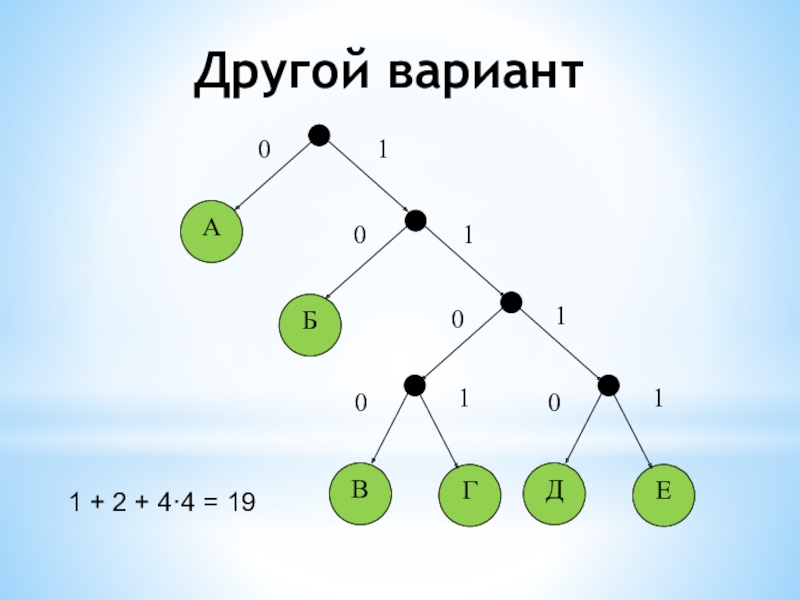
- 20. Другой вариант1 + 2 + 4·4 = 19
- 21. Задание 4По каналу связи передаются сообщения, каждое
- 22. Задание 5Для кодирования некоторой последовательности, состоящей из
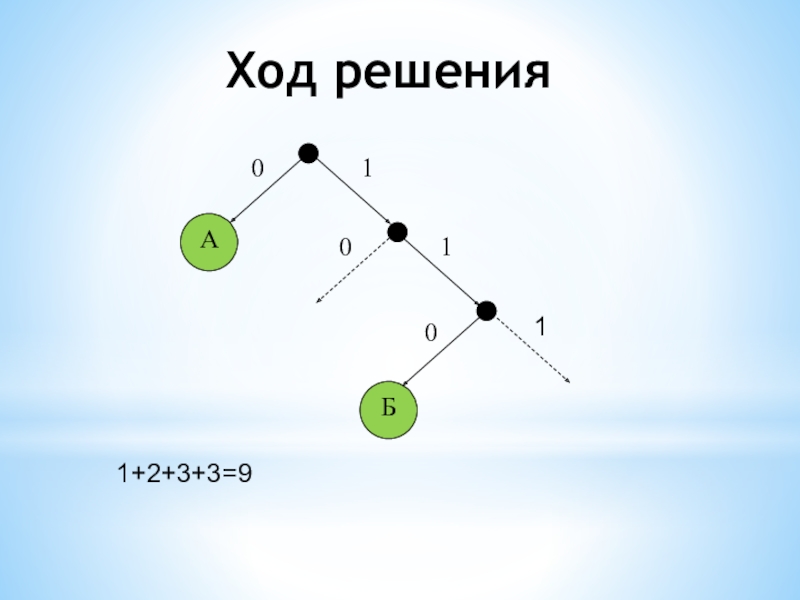
- 23. Ход решения11+2+3+3=9
- 24. Задание 6По каналу связи передаются сообщения, содержащие
- 25. Задание 7По каналу связи передаются сообщения, содержащие
- 26. Ход решения1
- 27. Ход решения1
- 28. Задание 8Для кодирования некоторой последовательности, состоящей из
- 29. Задание 9 По каналу связи передаются сообщения,
Кодированиеравномерноенеравномерное
Слайд 3Закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано:
никакое кодовое слово не является началом другого кодового слова.
Слайд 4Закодированное сообщение можно однозначно декодировать с конца, если выполняется обратное условие
Фано: никакое кодовое слово не является окончанием другого кодового слова
Слайд 5Пример 1
Пусть для кодирования первых 5 букв русского алфавита используется таблица:
Раскодируйте
сообщение:
1100000100110
1100000100110
Слайд 11Задание 1
Для кодирования некоторой последовательности, состоящей из букв А, Б, В,
Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением
Слайд 13Задание 2
По каналу связи с помощью равномерного двоичного кода передаются сообщения,
содержащие только 4 буквы: X, Y, Z, W; для кодировки букв используются кодовые слова длины 5. При этом для набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех. Для кодирования букв X, Y, Z используются 5-битовые кодовые слова:
X: 01111, Y: 00001, Z: 11000. Определите 5-битовое кодовое слово для буквы W, если известно, что оно начинается с 1 и заканчивается 0.
X: 01111, Y: 00001, Z: 11000. Определите 5-битовое кодовое слово для буквы W, если известно, что оно начинается с 1 и заканчивается 0.
Слайд 15Решение
Найдем количество позиций, в которых отличается это кодовое слово от известных
кодовых слов букв X, Y и Z (расстояние Хэмминга):
X: 01111 Y: 00001 Z: 11000
W: 1***0 W: 1***0 W: 1***0
2+? 2+? 0+?
X: 01111 Y: 00001 Z: 11000
W: 1***0 W: 1***0 W: 1***0
2+? 2+? 0+?
Слайд 17Задание 3
Для кодирования некоторой последовательности, состоящей из букв А, Б, В,
Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0; для буквы Б – кодовое слово 10. Какова наименьшая возможная
сумма длин всех шести кодовых слов? Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
сумма длин всех шести кодовых слов? Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Слайд 21Задание 4
По каналу связи передаются сообщения, каждое из которых содержит 16
букв А, 8 букв Б, 4 буквы В и 4 буквы Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью. При выборе кода учитывались два требования:
а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование);
б) общая длина закодированного сообщения должна быть как можно меньше.
Какой код из приведённых ниже следует выбрать для кодирования букв А, Б, В и Г?
1) А:0, Б:10, В:110, Г:111
2) А:0, Б:10, В:01, Г:11
3) А:1, Б:01, В:011, Г:001
4) А:00, Б:01, В:10, Г:11
а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование);
б) общая длина закодированного сообщения должна быть как можно меньше.
Какой код из приведённых ниже следует выбрать для кодирования букв А, Б, В и Г?
1) А:0, Б:10, В:110, Г:111
2) А:0, Б:10, В:01, Г:11
3) А:1, Б:01, В:011, Г:001
4) А:00, Б:01, В:10, Г:11
Слайд 22Задание 5
Для кодирования некоторой последовательности, состоящей из букв А, Б, В,
Г, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0, для буквы Б – кодовое слово 110. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
1) 7 2) 8 3) 9 4) 10
1) 7 2) 8 3) 9 4) 10
Слайд 24Задание 6
По каналу связи передаются сообщения, содержащие только 5 букв А,
И, К, О, Т. Для кодирования букв используется неравномерный двоичный код с такими кодовыми словами:
А — 0, И — 00, К — 10, О — 110, Т — 111.
Среди приведённых ниже слов укажите такое, код которого можно декодировать только одним способом. Если таких слов несколько, укажите первое по алфавиту.
1) КАА 2) ИКОТА 3) КОТ 4) ни одно из сообщений не подходит
А — 0, И — 00, К — 10, О — 110, Т — 111.
Среди приведённых ниже слов укажите такое, код которого можно декодировать только одним способом. Если таких слов несколько, укажите первое по алфавиту.
1) КАА 2) ИКОТА 3) КОТ 4) ни одно из сообщений не подходит
Слайд 25Задание 7
По каналу связи передаются сообщения, содержащие только 4 буквы П,
О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100.
Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Слайд 28Задание 8
Для кодирования некоторой последовательности, состоящей из букв А, Б, В,
Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны.
Каким из указанных способов это можно сделать?
1) для буквы В – 101 2) это невозможно
3) для буквы В – 010 4) для буквы Б – 10
Каким из указанных способов это можно сделать?
1) для буквы В – 101 2) это невозможно
3) для буквы В – 010 4) для буквы Б – 10
Слайд 29Задание 9
По каналу связи передаются сообщения, содержащие только 4 буквы:
А, И, С, Т.
В любом сообщении больше всего букв А, следующая по частоте буква – С, затем – И. Буква Т встречается реже, чем любая другая. Для передачи сообщений нужно использовать неравномерный двоичный код, допускающий однозначное декодирование; при этом сообщения должны быть как можно короче. Шифровальщик может использовать один из перечисленных ниже кодов. Какой код ему следует выбрать?
А – 0, И – 1, С – 00, Т – 11
2) С – 1, И – 0, А – 01, Т – 10
3) А – 1, И – 01, С – 001, Т – 000
4) С – 0, И – 11, А – 101, Т – 100
В любом сообщении больше всего букв А, следующая по частоте буква – С, затем – И. Буква Т встречается реже, чем любая другая. Для передачи сообщений нужно использовать неравномерный двоичный код, допускающий однозначное декодирование; при этом сообщения должны быть как можно короче. Шифровальщик может использовать один из перечисленных ниже кодов. Какой код ему следует выбрать?
А – 0, И – 1, С – 00, Т – 11
2) С – 1, И – 0, А – 01, Т – 10
3) А – 1, И – 01, С – 001, Т – 000
4) С – 0, И – 11, А – 101, Т – 100