- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по информатике на тему: Алгебра высказываний (8-9 классы)
Содержание
- 1. Презентация к уроку по информатике на тему: Алгебра высказываний (8-9 классы)
- 2. Простые высказывания обозначают заглавными латинскими буквами A,
- 3. Примеры:Рассмотрим следующие высказывания:A = (7 > 3)B
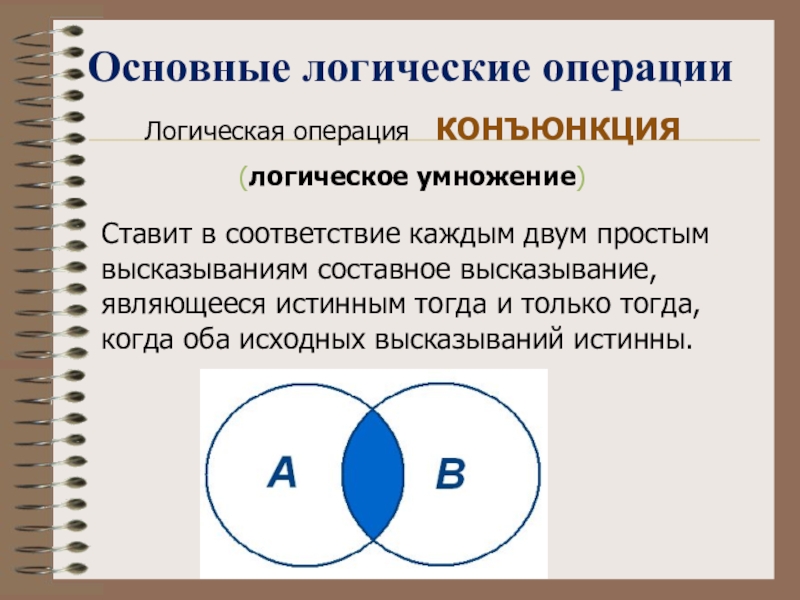
- 4. Основные логические операцииЛогическая операция КОНЪЮНКЦИЯ(логическое умножение)Ставит
- 5. КОНЪЮНКЦИЯ – логическое умножениеОбъединение двух или нескольких
- 6. КОНЪЮНКЦИЯЛОГИЧЕСКОЕ УМНОЖЕНИЕОПРЕДЕЛЯЕТ СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ С ПОМОЩЬЮ
- 7. Значение такого выражения будет ЛОЖЬ, если хотя
- 8. ТАБЛИЦА ИСТИННОСТИЗначения логической функции можно определить с
- 9. Построим таблицу истинности
- 10. Ленинград расположен на Неве и 2 +
- 11. ДИЗЪЮНКЦИЯ – логическое сложениеОбъединение двух или нескольких
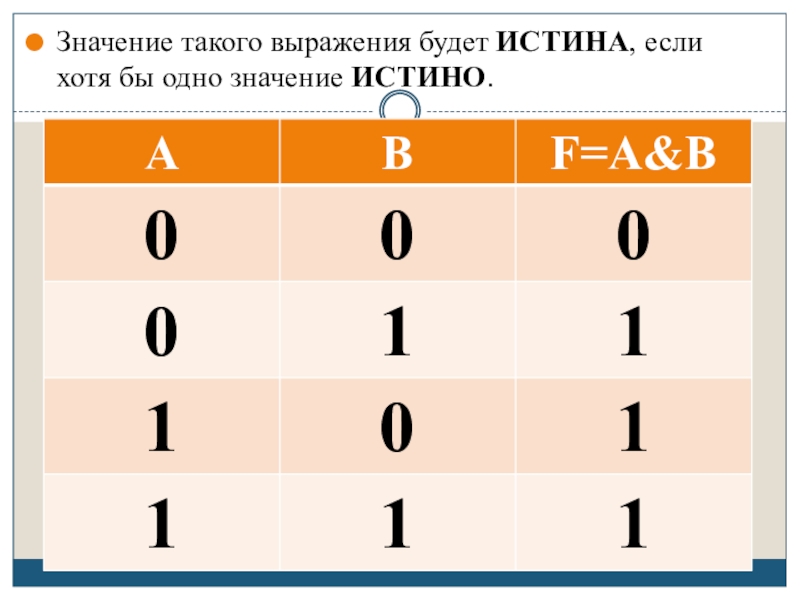
- 12. Значение такого выражения будет ИСТИНА, если хотя бы одно значение ИСТИНО.
- 13. Дизъюнкция - логическая операция, которая каждым двум
- 14. 7 – простое число или 9 –
- 15. РЕШИМ ЗАДАЧИМарина и Оля старше Светы.Половина класса
- 16. ИНВЕРСИЯ – логическое отрицаниеПрисоединение частицы «НЕ» к
- 17. Инверсия - логическая операция, которая каждому высказыванию
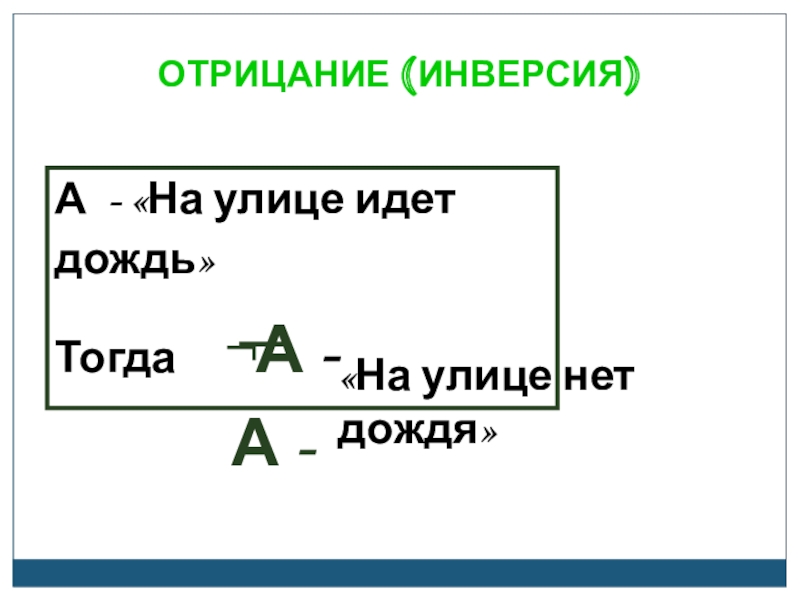
- 18. ОТРИЦАНИЕ (ИНВЕРСИЯ)А - «На улице идет дождь»Тогда
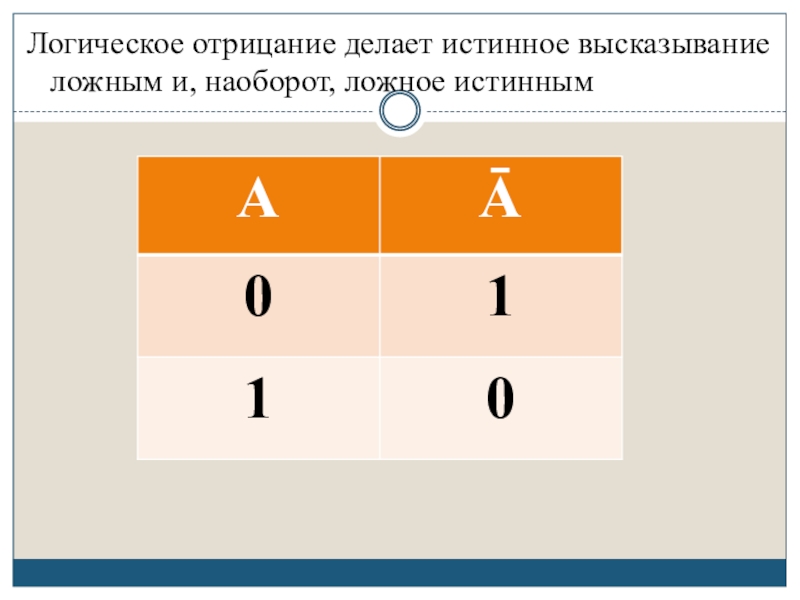
- 19. Логическое отрицание делает истинное высказывание ложным и, наоборот, ложное истинным
- 20. Последовательность выполнения операций в логических формулах определяется
- 21. определите, в каком порядке необходимо вычислять значение
- 22. Выделите в составных высказываниях простые. Запишите с
- 23. Найти значения логических выражений(1v1)v(1v0);(0v1)v(1v0);1&(1&1)&1;((1&0)&(1&1))&(0v1);((1&1)v0)&(0v1)
- 24. Даны два простых высказывания: A = {2*2
- 25. Пусть А = «На Web-странице встречается слово
- 26. 5000000 – 7000 = 4 993 000
- 27. Домашнее задание§1.3; задание №10 к параграфу; РТ № 53-56.
Слайд 2Простые высказывания обозначают
заглавными латинскими буквами
A, B, C…X, Y, Z
логическими переменными
Значения высказываний
ИСТИНА или ЛОЖЬ обозначают
соответственно цифрами 1 и 0
и называют логическими величинами
Составные высказывания называются
логическими выражениями и включают
в себя логические переменные,
операции логики и скобки для изменения
порядка действий операций
Слайд 3Примеры:
Рассмотрим следующие высказывания:
A = (7 > 3)
B = (7 = 3)
C
D = (B ۸ C) = ((7 = 3) ۸ (7 ≠ 3))
На языке алгебры логики эти высказывания можно записать так:
A = ИСТИНА = 1
B = ЛОЖЬ = 0
C = ИСТИНА = 1
D = ЛОЖЬ = 0
Слайд 4Основные логические операции
Логическая операция КОНЪЮНКЦИЯ
(логическое умножение)
Ставит в соответствие каждым двум
Слайд 5КОНЪЮНКЦИЯ – логическое умножение
Объединение двух или нескольких высказываний в одно с
В алгебре логики знак & (амперсенд);
В программировании and или ^;
Конъюнкция – двухместная операция, записывается
А^В; F=A&B;
Слайд 6КОНЪЮНКЦИЯ
ЛОГИЧЕСКОЕ УМНОЖЕНИЕ
ОПРЕДЕЛЯЕТ СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ С ПОМОЩЬЮ СОЮЗА
И
В прямоугольнике противоположные стороны
В прямоугольнике противоположные стороны равны и пересекаются
1
0
&
^
Слайд 7Значение такого выражения будет ЛОЖЬ, если хотя бы значение одного из
Пример:
Число 6 делится на 2, и число 6 делится на 3;
Число 6 делится на 2= А;
Число 6 делится на 3= В;
F=A&B=1 (истина)
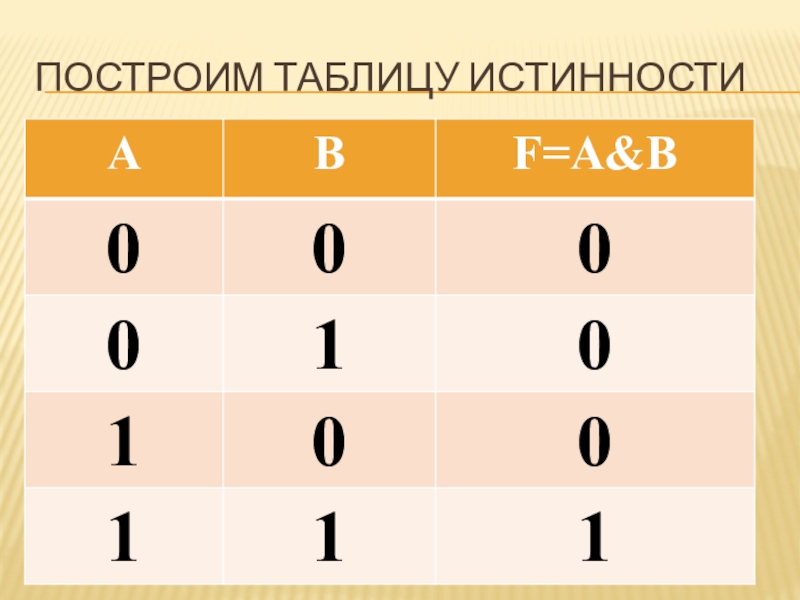
Слайд 8ТАБЛИЦА ИСТИННОСТИ
Значения логической функции можно определить с помощью таблицы истинности, которая
Слайд 10Ленинград расположен на Неве и 2 + 3 = 5
7 –
2 * 2 = 4 и 2 * 2 ≤ 5 и 2 * 2 ≥ 4
Москва – столица России и Екатеринбург – столица Сибири
Книга – источник информации и 5 не больше 8
Девочки обычно любят играть в куклы и Не любая машина - автомобиль
Все гуси – птицы и Все игрушки - машины
Ответ: истинными высказываниями являются: 1, 3, 5, 6
Определить значения истинности следующих высказываний:
Слайд 11ДИЗЪЮНКЦИЯ – логическое сложение
Объединение двух или нескольких высказываний в одно с
В алгебре логики знак ; +;
В программировании OR;
Дизъюнкция – двухместная операция, записывается
А В;
^
^
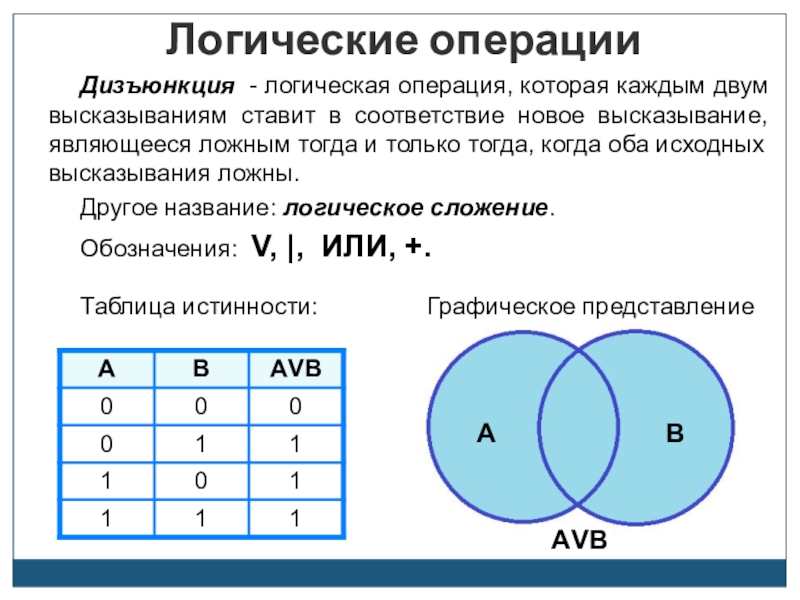
Слайд 13Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие
Другое название: логическое сложение.
Обозначения: V, |, ИЛИ, +.
Логические операции
Таблица истинности:
Графическое представление
A
B
АVВ
Слайд 147 – простое число или 9 – простое число
Число 2 четное
2 * 2 = 4 или Белые медведи живут в Африке
Каша – вкусное блюдо или Математика – интересный предмет
Луна – спутник Марса или Луна – спутник Земли
Сегодня плохая погода или Кислород – вода
Microsoft Word – текстовый редактор или Paint – графический редактор
Ответ: истинными высказываниями являются: 1, 2, 3, 5, 7
Определить значения истинности следующих высказываний:
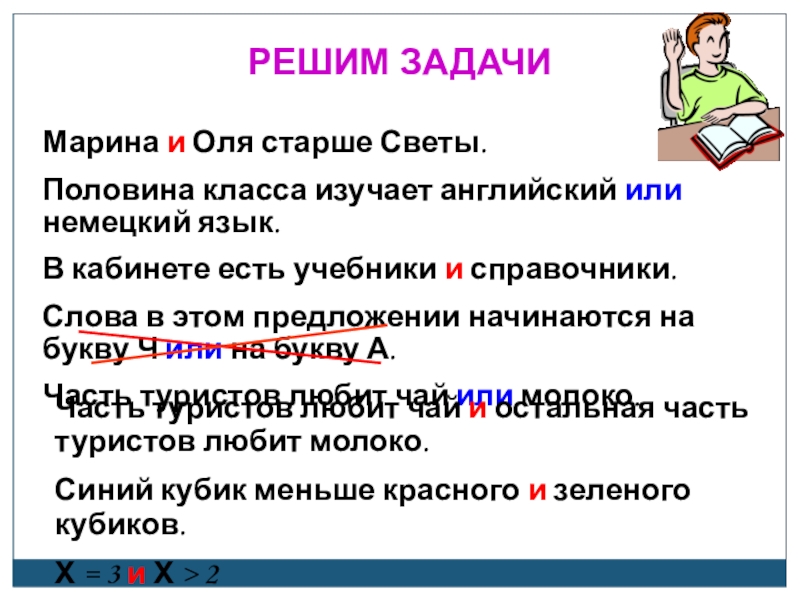
Слайд 15РЕШИМ ЗАДАЧИ
Марина и Оля старше Светы.
Половина класса изучает английский или немецкий
В кабинете есть учебники и справочники.
Слова в этом предложении начинаются на букву Ч или на букву А.
Часть туристов любит чай или молоко.
Часть туристов любит чай и остальная часть туристов любит молоко.
Синий кубик меньше красного и зеленого кубиков.
Х = 3 и Х > 2
Слайд 16ИНВЕРСИЯ – логическое отрицание
Присоединение частицы «НЕ» к высказыванию, называется операцией логического
В естественном языке соответствует словам неверно, что…; частица НЕ;
Обозначение Ā;
На языке программирования Not
Отрицание – (унарная) одноместная операция
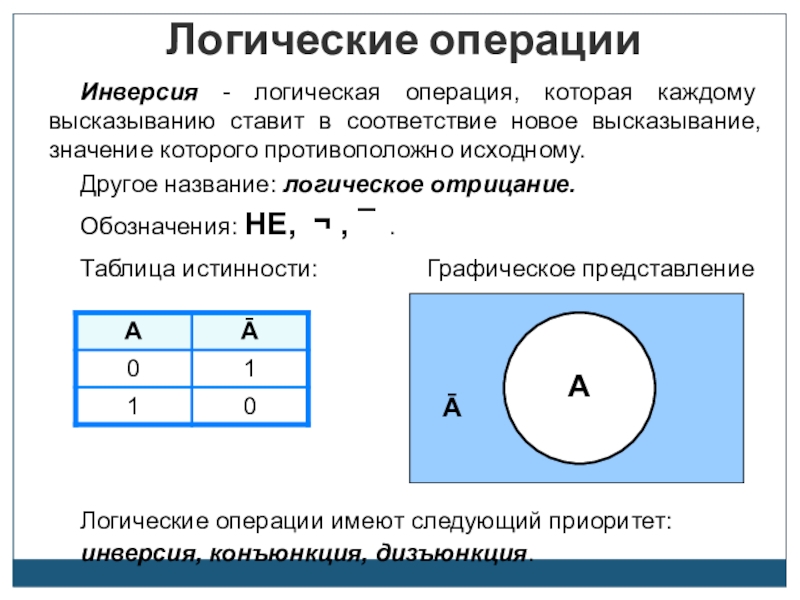
Слайд 17Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое
Другое название: логическое отрицание.
Обозначения: НЕ, ¬ , ¯ .
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция.
Логические операции
Таблица истинности:
Графическое представление
A
Ā
Слайд 20Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке
отрицание, конъюнкция, дизъюнкция.
Кроме того, на порядок операции влияют скобки, которые можно использовать в логических формулах.
Слайд 21определите, в каком порядке необходимо вычислять значение логического выражения:
¬ А &
A & (B & C)
(A & B) ν (C & ¬ D)
A ν ¬ D ν B
A ^ B ^ ¬ A
РЕШИМ ЗАДАЧИ
Слайд 22Выделите в составных высказываниях простые. Запишите с помощью логических операций каждое
Число 376 чётное и трёхзначное.
Неверно, что Солнце движется вокруг Земли
Слайд 23Найти значения логических выражений
(1v1)v(1v0);
(0v1)v(1v0);
1&(1&1)&1;
((1&0)&(1&1))&(0v1);
((1&1)v0)&(0v1)
Слайд 24Даны два простых высказывания: A = {2*2 = 4}, B = {2*2
Какие из составных высказываний истины:
а) Ā ; б) ;
в) A & B; г) A v B
Слайд 25Пусть А = «На Web-странице встречается слово "крейсер"», В = «На
В некотором сегменте сети Интернет 5 000 000 Web-страниц. В нём высказывание А истинно для 4800 страниц, высказывание В - для 4500 страниц, а высказывание АVВ - для 7000 страниц.
Для какого количества Web-страниц в этом случае будут истинны следующие выражения и высказывание?
а) НЕ (А ИЛИ В);
б) А & B;
в) На Web-странице встречается слово "крейсер" И НЕ встречается слово "линкор".
Решаем задачу
Слайд 265000000 – 7000 = 4 993 000 Web-страниц НЕ (А ИЛИ
A = 4800, B = 4500.
4800 + 4500 = 9300
4800 – 2300 = 2500 Web-страниц
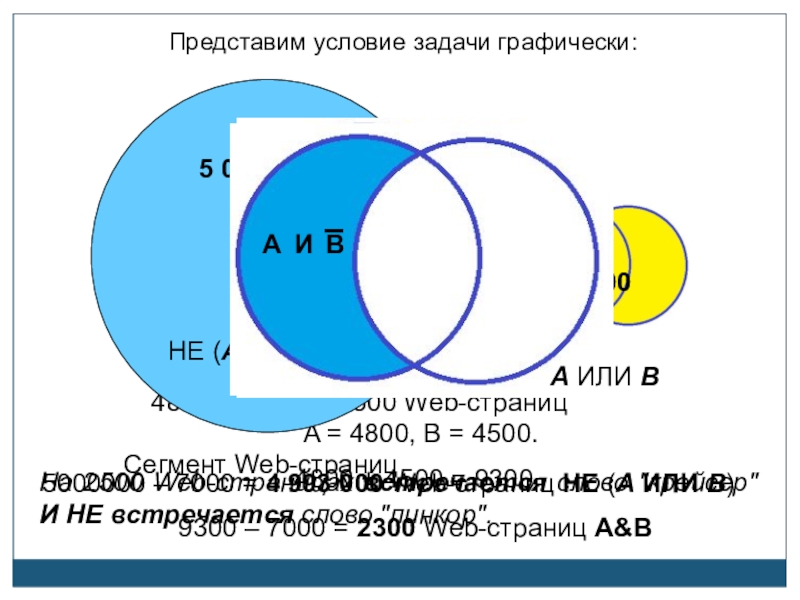
Представим условие задачи графически:
На 2500 Web-страницах встречается слово "крейсер" И НЕ встречается слово "линкор".
5 000 000
7 000
НЕ (А ИЛИ В)
Сегмент Web-страниц
A
B
A&B
9300 – 7000 = 2300 Web-страниц A&B
A
И
А ИЛИ В