- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку информатики для 10 класса. Тема Логические законы и правила преобразования логических выражений
Содержание
- 1. Презентация к уроку информатики для 10 класса. Тема Логические законы и правила преобразования логических выражений
- 2. Содержание1. Виды мышления и алгебра высказываний (Задания
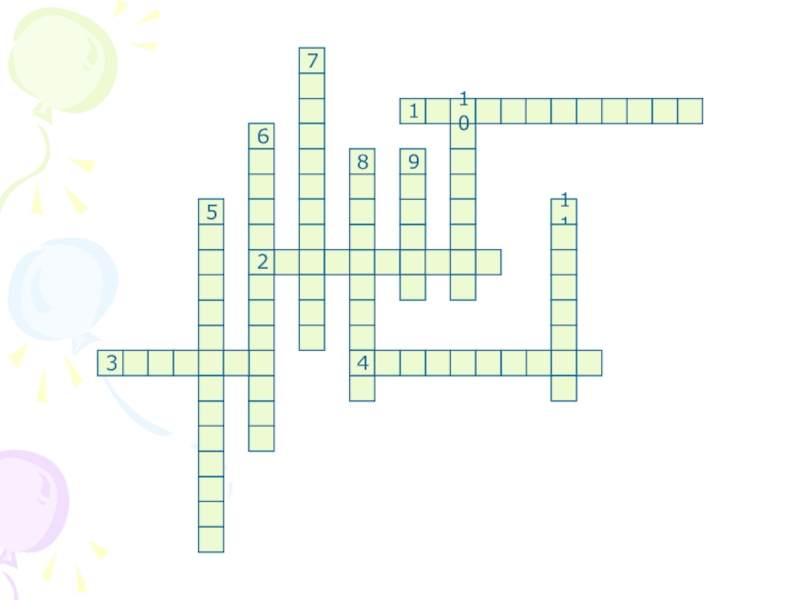
- 3. КроссвордПо горизонтали:Это повествовательное предложение, о котором можно
- 4. 7298410111635
- 5. ЗАДАЧА 1 Постройте отрицания следующих высказываний:Сегодня мы
- 6. ЗАДАЧА 2 Пусть р = «Марии
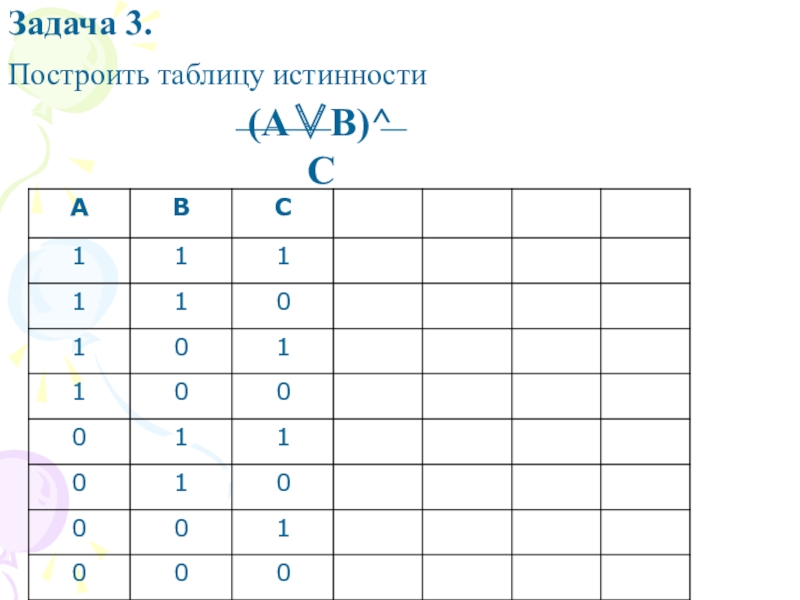
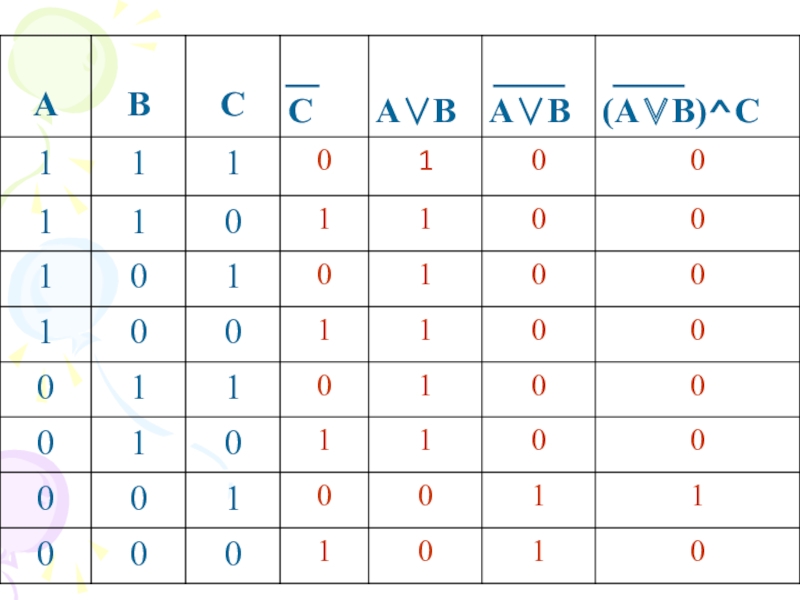
- 7. (A∨B)^CЗадача 3. Построить таблицу истинности
- 8. Слайд 8
- 9. Логические законы и правила
- 10. 4.Закон двойного отрицанияЕсли дважды отрицать некоторое высказывание, то получим исходное высказываниеА = А
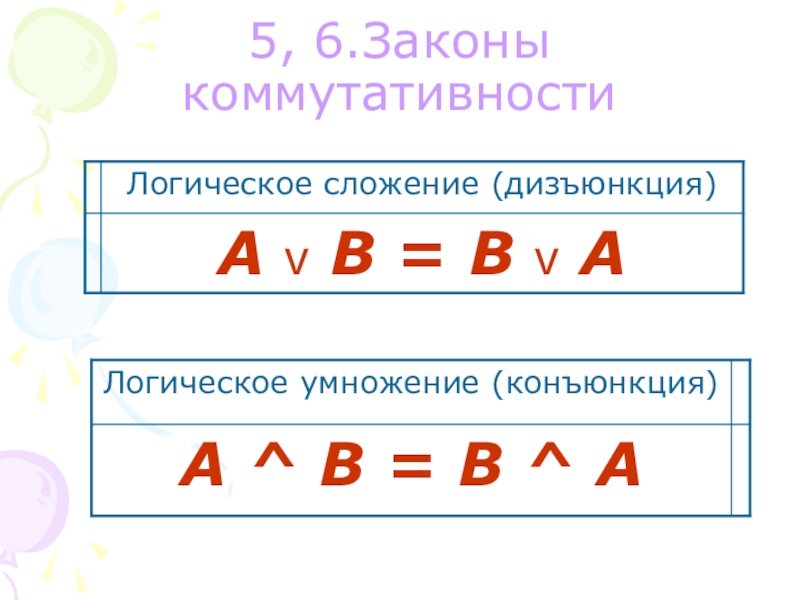
- 11. 5, 6.Законы коммутативности
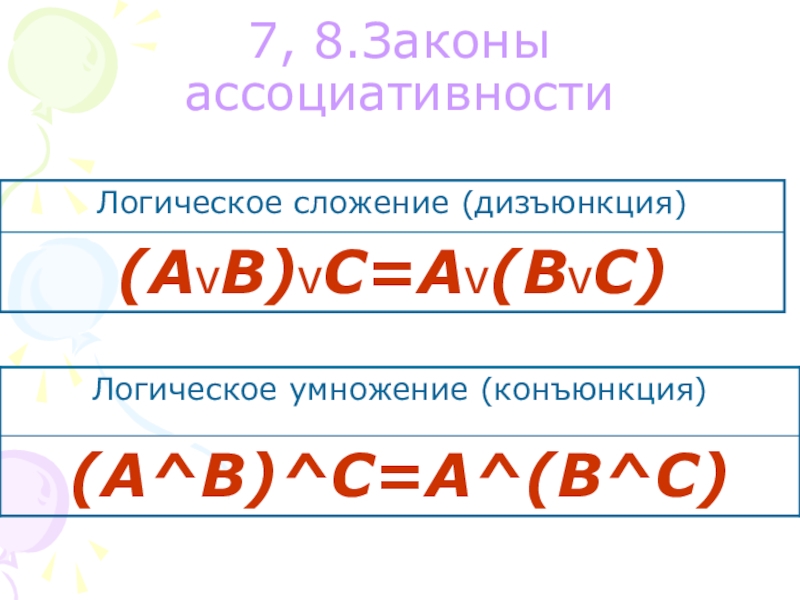
- 12. 7, 8.Законы ассоциативности
- 13. 9, 10.Законы дистрибутивности
- 14. 11, 12. Законы поглощения Для логического умножения A^(A v B)=AДля логического сложенияA v (A^B)=A
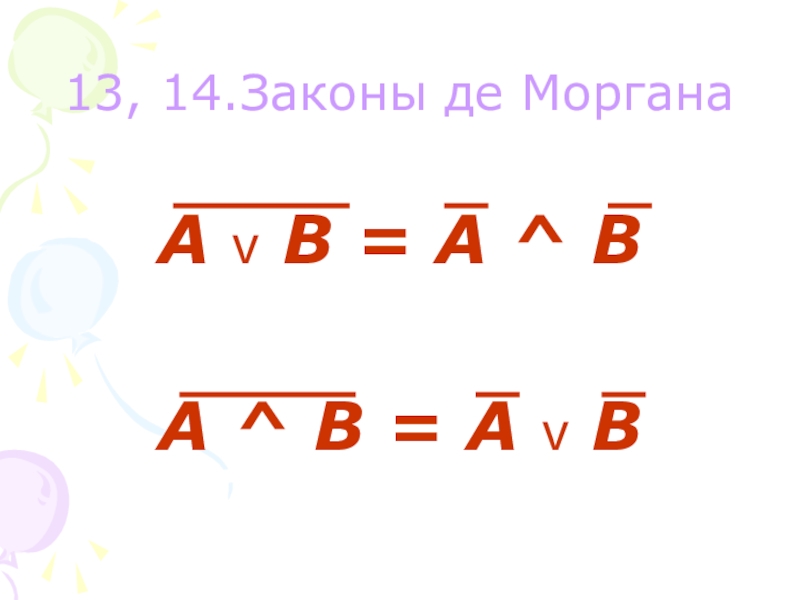
- 15. 13, 14.Законы де МорганаА v В =
- 16. 15. Удаление импликацииA→B=A v B
- 17. 16. Определение импликацииA↔B=(A→B)^(B→A)
- 18. 17. Правила равносильности А v A = А A ^ A = A
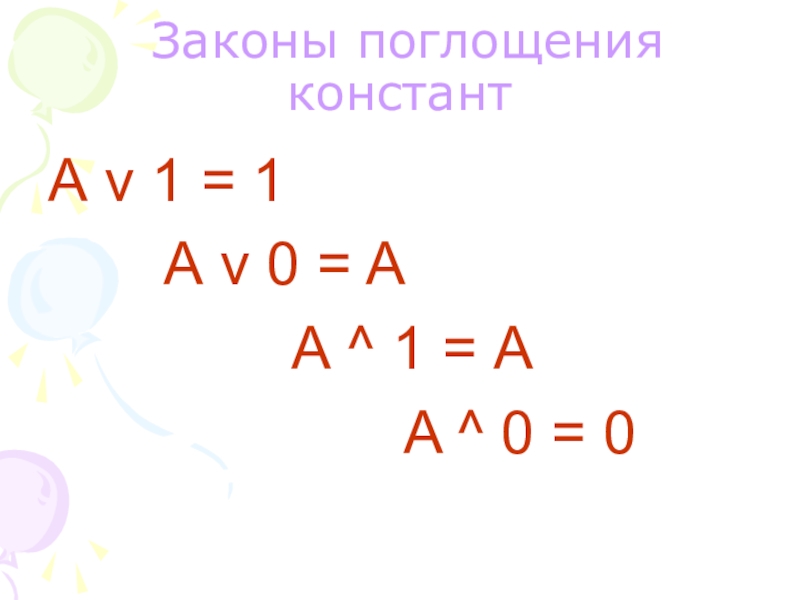
- 19. Законы поглощения константА v 1 =
- 20. Задание 1. Упростить выражение:
- 21. Найти значение логической переменной Х из
- 22. Закрепление изученного№1Упростите выражение:F = (A^B) v (BvC).F
- 23. Домашняя работаУпростите логические выражения: F = Av
- 24. Спасибо за внимание!!!
Слайд 2Содержание
1. Виды мышления и алгебра высказываний (Задания на повторение)
а) Кроссворд (основные
б) Задача 1 (построение отрицания)
в) Задача 2 (высказывания на естественном языке)
г) Задача 3 (построение таблицы истинности)
Логические законы и правила преобразования логических выражений (изучение нового материала)
а) Теоретическая часть
б) Задача 1 (Пример упрощения)
в) Задача 2 (Найти значение переменной Х с помощью рассмотренных законов и правил)
г) Решение задач (закрепление изученного)
д) Домашнее задание
Слайд 3Кроссворд
По горизонтали:
Это повествовательное предложение, о котором можно сказать, истинно оно или
Логическое умножение.
Форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов.
Логическая операция, которая обозначается значком →
По вертикали:
мыслительный процесс, направленный на подтверждение или опровержение какого-либо положения посредством других несомненных, ранее обоснованных доводов.
Прием мышления, посредством которого из исходного знания получается новое знание.
Логическая операция, которой в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае…
Логическое сложение.
Наука о законах и формах мышления.
Мысль, в которой что-либо утверждается или отрицается.
Отрицание.
Слайд 5ЗАДАЧА 1
Постройте отрицания следующих высказываний:
Сегодня мы идем на балет «Щелкунчик".
Каждый рыбак
Неверно, что число 2 не является делителем числа 24.
Аркадий решил все примеры домашней работы.
Сегодня мы не идем на балет «Щелкунчик».
Не каждый рыбак желает поймать большую рыбу
(некоторые рыбаки не желают поймать большую рыбу).
Число 2 не является делителем числа 24
Неверно, что Аркадий решил все примеры домашней работы
(Аркадий не решил некоторые задания домашней работы).
Слайд 6ЗАДАЧА 2 Пусть р = «Марии нравятся уроки рисования», а
Выразите следующие формулы
на обычном языке:
^
^
^
^
^
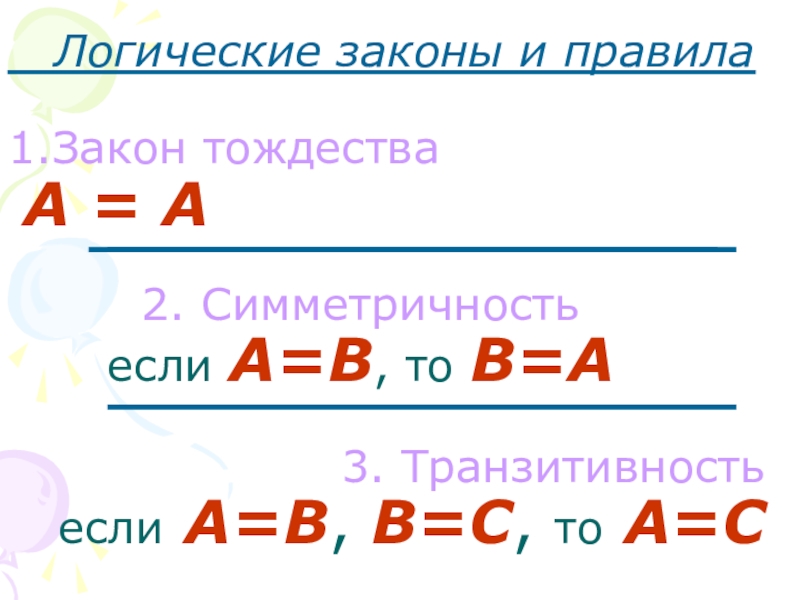
Слайд 9 Логические законы и правила
1.Закон тождества
А = А
2. Симметричность
если
3. Транзитивность
если А=B, B=C, то A=C
Слайд 104.Закон двойного отрицания
Если дважды отрицать некоторое высказывание, то получим исходное высказывание
А
Слайд 1411, 12. Законы поглощения
Для логического умножения
A^(A v B)=A
Для логического
A v (A^B)=A
Слайд 20Задание 1. Упростить выражение:
Воспользуемся распределительным законом:
A ^ ( B v C ) = A ^ B v A ^ C
1
X ^ Y v X ^ Y =
X ^ (Y v Y ) =
= Х ^ 1 = Х
Слайд 21Найти значение логической переменной Х
из логического уравнения
Х
(Х v Y) v (X v Y) = Z
(Х ^ Y) v (X ^ Y) = Z
Х ^ (Y v Y) = Z
Х ^ 1 = Z
Х = Z
Х = Z
Задание 2.
Слайд 22Закрепление изученного
№1
Упростите выражение:
F = (A^B) v (BvC).
F = (A→B) v (B→A).
F
F =AvBvCvAvBvC
Ответы:
F = (A^B) v (BvC) =AvB.
F= (A→B) v (B→A) = 1.
F = A ^ C v Ā ^C=C.
F =AvBvCvAvBvC=1.
Слайд 23Домашняя работа
Упростите логические выражения:
F = Av (A^B).
F = A^ (AvB).
F
F = (1 V (AvB)) V ((AvC) ^ 1).