- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Измерение информации. Содержательный подход
Содержание
- 1. Презентация. Измерение информации. Содержательный подход
- 2. Как можно измерить количество информации?
- 3. Неопределенность знания и количество информацииДругой подход к
- 4. СОДЕРЖАТЕЛЬНЫЙ ПОДХОД К ИЗМЕРЕНИЮ ИНФОРМАЦИИ
- 5. На книжном стеллаже восемь полок. Книга может
- 6. МЕТОД БИНАРНОГО ПОИСКАТребуется угадать задуманное число из
- 7. А сейчас попробуем получить формулу, по которой
- 8. С полученной формулой мы уже знакомы из
- 9. ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕNi Определение количества информации, содержащейся
- 10. Домашнее задание §4Индивидуальное заданиеСообщение: Клод Шеннон
- 11. КОЛИЧЕСТВО ИНФОРМАЦИИ В СООБЩЕНИИ Задача
- 12. Слайд 12
- 13. Слайд 13
Слайд 3Неопределенность знания и количество информации
Другой подход к измерению информации называют содержательным
В этом случае количество информации связывается с содержанием (смыслом) полученного человеком сообщения. Вспомним, что с «человеческой» точки зрения информация — это знания, которые мы получаем из внешнего мира. Количество информации, заключенное в сообщении, должно быть тем больше, чем больше оно пополняет наши знания.
Как же с этой точки зрения определяется единица измерения информации? Вы уже знаете, что эта единица называется битом. Проблема измерения информации исследована в теории информации, основатель которой — Клод Шеннон.
Слайд 4СОДЕРЖАТЕЛЬНЫЙ ПОДХОД К ИЗМЕРЕНИЮ ИНФОРМАЦИИ
Сообщение о том,
8 цветных шаров в корзине – 8 равновероятных событий
Неопределенность знания о том, что из корзины может быть извлечен шар красного цвета, равна 8.
Более строгое определение равновероятности: если увеличивать количество бросаний монеты (100, 1000, 10000 и т. д.), то число выпадений орла и число выпадений решки будут все ближе к половине количества бросаний монеты.
Следовательно, можно сказать так:
Неопределенность знания о результате некоторого события (бросание монеты или игрального кубика, вытаскивание жребия и др.) — это количество возможных результатов.
Слайд 5На книжном стеллаже восемь полок. Книга может быть поставлена на любую
Сколько информации содержит сообщение о том, где находится книга?
Задаем вопросы:
- Книга лежит выше четвертой полки?
- Нет.
- Книга лежит ниже третьей полки?
- Да .
- Книга — на второй полке?
- Нет.
- Ну теперь все ясно! Книга лежит на первой полке!
Каждый ответ уменьшал неопределенность в два раза.
Всего было задано три вопроса. Значит, набрано 3 бита информации.
И если бы сразу было сказано, что книга лежит на первой полке,
то этим сообщением были бы переданы те же 3 бита информации.
Слайд 6
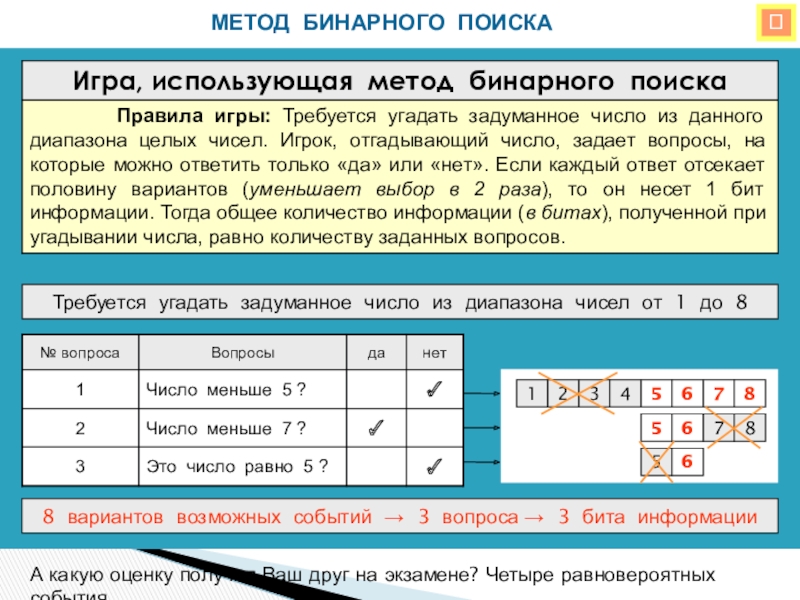
МЕТОД БИНАРНОГО ПОИСКА
Требуется угадать задуманное число из диапазона чисел от 1
8 вариантов возможных событий 3 вопроса 3 бита информации
А какую оценку получил Ваш друг на экзамене? Четыре равновероятных события.
Слайд 7А сейчас попробуем получить формулу, по которой вычисляется количество информации, содержащейся
Обозначим буквой N количество возможных результатов события, или, как мы это еще называли, — неопределенность знания. Буквой i будем обозначать количество информации в сообщении об одном из N результатов.
В примере с монетой: N = 2, i = 1 бит.
В примере с оценками: N = 4, i = 2 бита.
В примере со стеллажом: N = 8, i = 3 бита.
Нетрудно заметить, что связь между этими величинами выражается следующей формулой:
2i = N.
Действительно: 21 = 2 ; 22 = 4 ; 23 = 8.
Слайд 8С полученной формулой мы уже знакомы из базового курса информатики, и
2i = N.
Поскольку 16 = 2 , то i = 4 бита.
Количество информации (i), содержащееся в сообщении об одном из N равновероятных результатов некоторого событий, определяется из решения показательного уравнения: 2i = N.
Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему, например, равно количество информации в сообщении о результате бросания игральной кости, у которой имеется шесть граней и, следовательно, N = 6? Можно догадаться, что решение уравнения 2i = 6.
будет дробным числом, лежащим между 2 и 3, поскольку 22 = 4 < 6, а 2 = 8 > 6. А как точнее узнать это число?
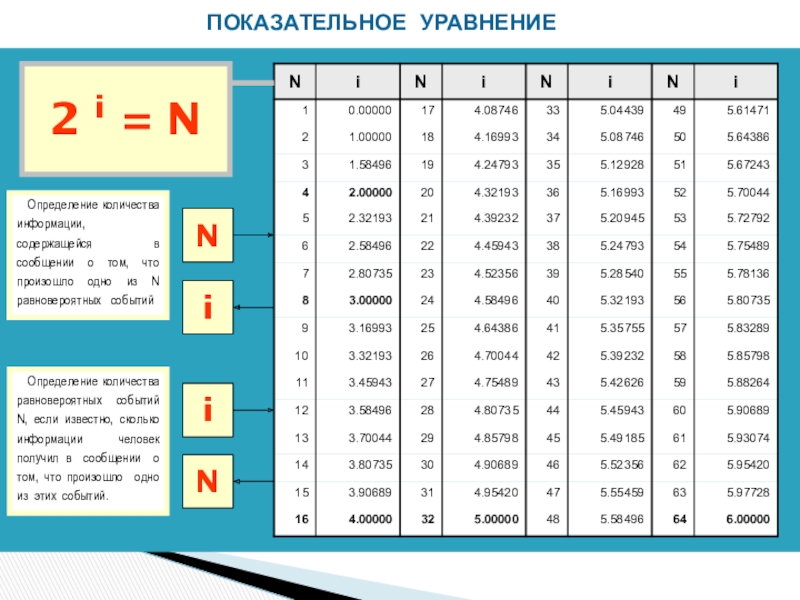
Слайд 9ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕ
N
i
Определение количества информации, содержащейся в сообщении о том,
N
i
Определение количества равновероятных событий N, если известно, сколько информации человек получил в сообщении о том, что произошло одно из этих событий.
2 i = N
Слайд 11
КОЛИЧЕСТВО ИНФОРМАЦИИ В СООБЩЕНИИ
Задача 1. При угадывании
было получено 6 бит информации . Чему равно N ?
Решение задачи 1. Значение N определяется из формулы N = 2 i .
После подстановки значения i = 6 получаем: N = 2 6 = 64.
Задача 2. В корзине лежат 16 шаров разного цвета . Сколько информации несет сообщение о том , что из корзины достали красный шар ?
Решение задачи 2: Вытаскивание из корзины любого из 16 шаров – события равновероятные. Поэтому для решения задачи применима формула 2 i = N. Здесь N = 16 – число шаров. Решая уравнение 2 I =16 получаем ответ: i = 4 бита
2 i = N
N
i
Количество равновероятных возможных событий
Количество информации в сообщении о том, что произошло одно из N равновероятных событий.