- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для 9 класса на тему Основы логики.Формы мышления
Содержание
- 1. Презентация для 9 класса на тему Основы логики.Формы мышления
- 2. Формы мышленияПервые учёные о формах и способах
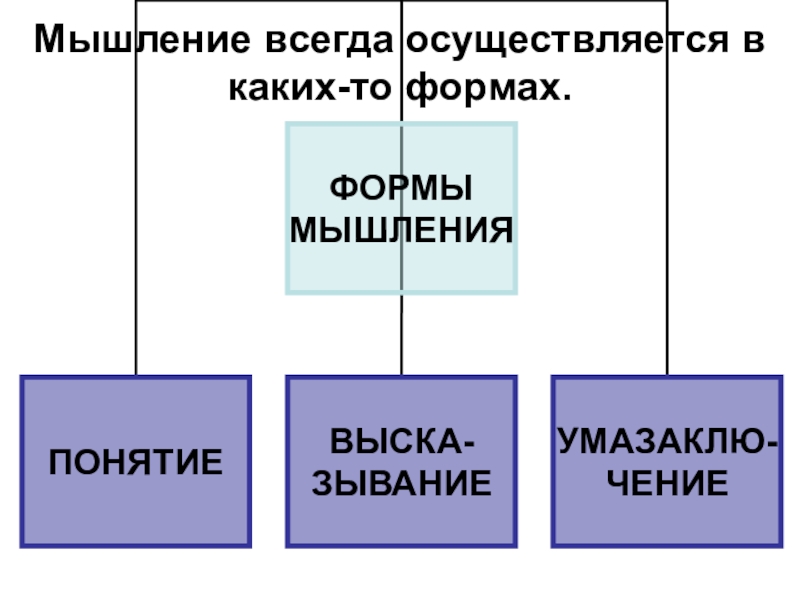
- 3. Мышление всегда осуществляется в каких-то формах.
- 4. ПОНЯТИЕПОНЯТИЕ – это форма мышления, фиксирующая основные,
- 5. Понятие имеет 2 стороны: содержание и объём.
- 6. ВЫСКАЗЫВАНИЕВЫСКАЗЫВАНИЕ – это форма мышления, в котором
- 7. Слайд 7
- 8. УМОЗАКЛЮЧЕНИЕУМОЗАКЛЮЧЕНИЕ – это форма мышления, с помощью
- 9. Алгебра высказыванийЗдесь высказывания обозначаются именами логических переменных(А,
- 10. Логическое умножение (конъюнкция)Высказывания объединяются с помощью союза
- 11. Логическое сложение (дезъюнкция)Высказывания объединяются с помощью союза
- 12. Логическое отрицание (инверсия)Присоединение частицы «НЕ» к высказыванию.
- 13. Порядок выполнения операцийСкобкахОтрицаниеЛогическое умножениеЛогическое сложение
- 14. ЛОГИЧЕСКИЕФУНКЦИИ
- 15. В обыденной и научной речи кроме базовых
- 16. Логическое следование (импликация)Логическое следование (импликация) образуется соединением
- 17. Составное высказывание, образо-ванное с помощью операции логического
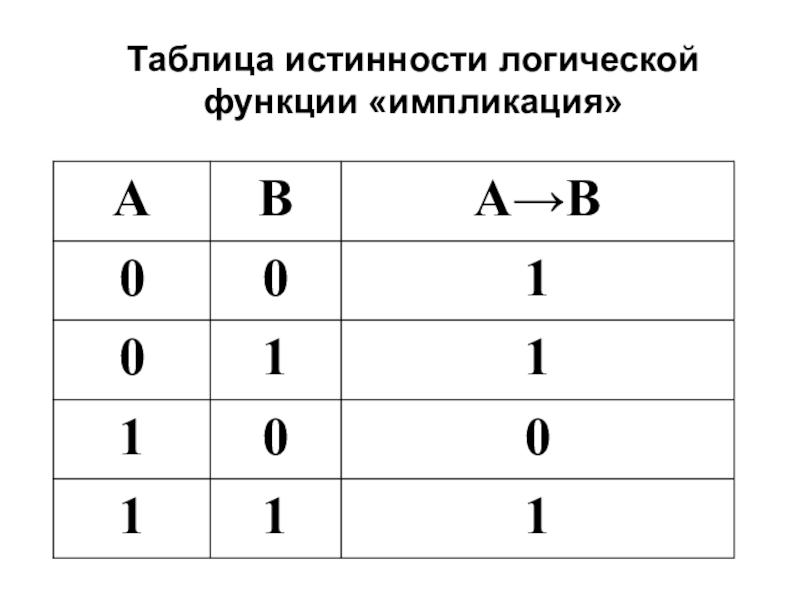
- 18. Таблица истинности логической функции «импликация»
- 19. Например, высказывание «Если число делится на 10,
- 20. Однако операция логического следования несколько отличается от
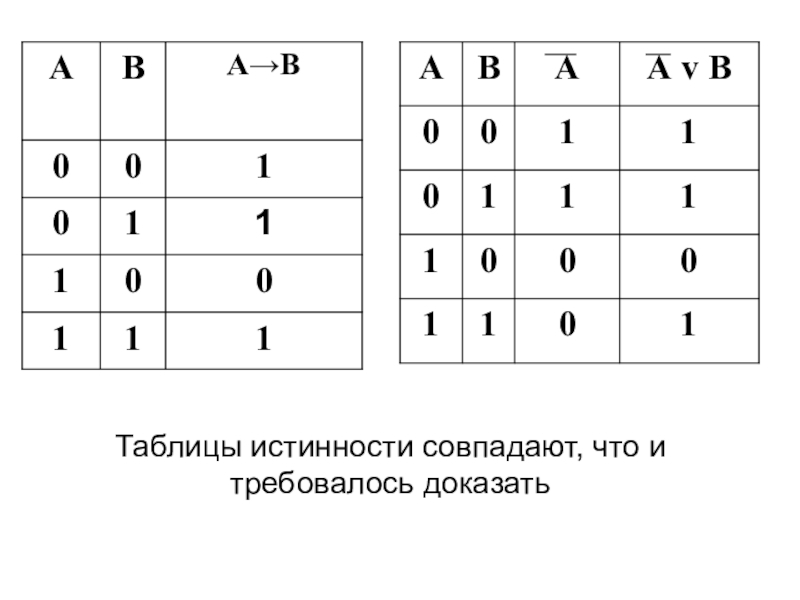
- 21. Доказать методом сравнения таблиц истинности, что операция импликации А→В равносильна логическому выражению А v В.
- 22. Таблицы истинности совпадают, что и требовалось доказать
- 23. Логическое равенство (эквивалентность)Логическое равенство (эквивалентность) образуется соединением
- 24. Составное высказывание, образованное с помощью логической операции
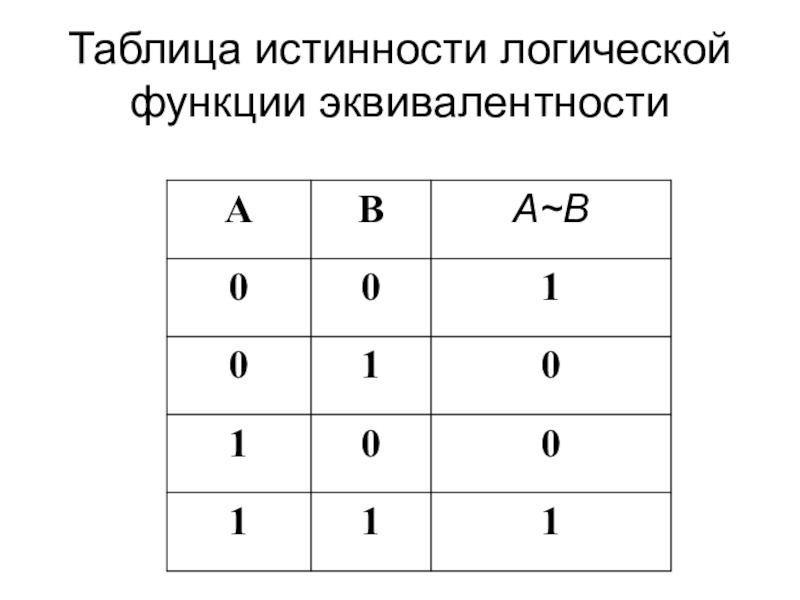
- 25. Таблица истинности логической функции эквивалентности
- 26. Рассмотрим, например, два высказывания: А = «Компьютер
- 27. Составное высказывание, полученное с помощью операции эквивалентности,
- 28. Приоритет операций:Инверсия (отрицание);Конъюнкция (умножение);Дизъюнкция (сложение);Импликация (следование) и эквивалентность (равенство).
Формы мышленияПервые учёные о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия).Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.ЛОГИКА – это наука о формах и способах мышления.
Слайд 2Формы мышления
Первые учёные о формах и способах рассуждений возникли в странах
Древнего Востока (Китай, Индия).
Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.
Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.
ЛОГИКА – это наука о формах и способах мышления.
Слайд 4ПОНЯТИЕ
ПОНЯТИЕ – это форма мышления, фиксирующая основные, сущес-твенные признаки объекта.
Например, понятие
«компьютер» объединяет множество электронных устройств, которые предназначены для обработки информации.
Слайд 5Понятие имеет 2 стороны: содержание и объём.
Содержание понятия составляет сово-купность
существенных признаков объекта. («Персональный компьютер – это универ-сальное электронное устройство для автоматической обработки информации, предназначенное для 1 пользователя»)
Объём понятия определяется совокупностью предметов, на которую оно распространяется. («персональный компьютер» выражает всю совокупность(сотни миллионов)существующих в настоящее время в мире персональных компьютеров)
Объём понятия определяется совокупностью предметов, на которую оно распространяется. («персональный компьютер» выражает всю совокупность(сотни миллионов)существующих в настоящее время в мире персональных компьютеров)
Слайд 6ВЫСКАЗЫВАНИЕ
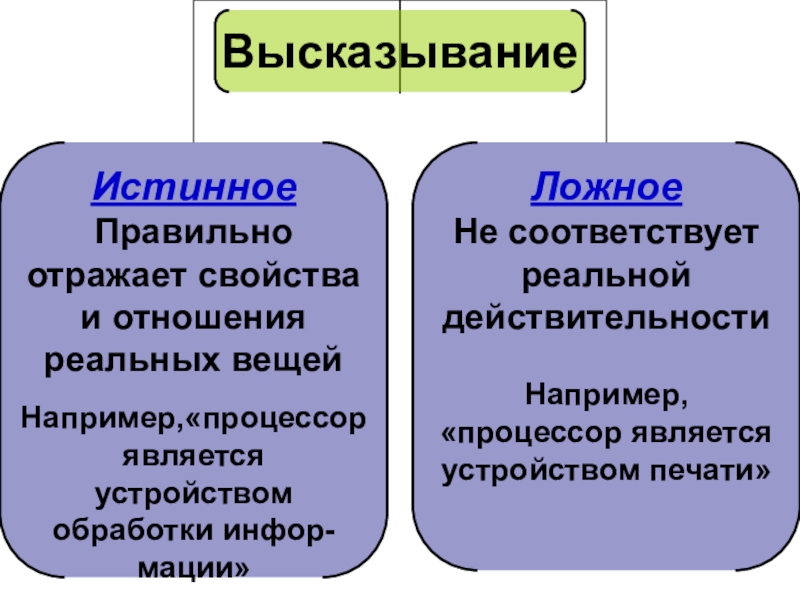
ВЫСКАЗЫВАНИЕ – это форма мышления, в котором что-либо утверждается или отрицается.
Высказывание
могут быть выражены с помощью не только естественных языков, но и формальных. Например, высказывание на естественном языке имеет вид «Два умножить на два равно четырём», а на формальном, математическом языке оно записывается в виде: «2•2=4»
Слайд 8УМОЗАКЛЮЧЕНИЕ
УМОЗАКЛЮЧЕНИЕ – это форма мышления, с помощью которой из одного или
нескольких суждений может быть получено новое суждение (заключение).
Например, Если «Все углы треугольника равны», то справедливо суждение «Этот треугольник равносторонний»
Например, Если «Все углы треугольника равны», то справедливо суждение «Этот треугольник равносторонний»
Слайд 9Алгебра высказываний
Здесь высказывания обозначаются именами логических переменных(А, В, С и т.д.),
которые могут принимать лишь 2 значения: «истина»(1) и «ложь»(0).
В алгебре высказываний над высказы-ваниями можно производить определённые логические операции, в результате которых получаются новые, составные высказывания. Для их образования используют базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
В алгебре высказываний над высказы-ваниями можно производить определённые логические операции, в результате которых получаются новые, составные высказывания. Для их образования используют базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Слайд 10Логическое умножение (конъюнкция)
Высказывания объединяются с помощью союза «И». Между высказываниями ставят
знак & либо ^
Истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
Таблица истинности функции логического умножения
Истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
Таблица истинности функции логического умножения
Слайд 11Логическое сложение (дезъюнкция)
Высказывания объединяются с помощью союза «ИЛИ». Между высказываниями ставят
знак + либо V
Истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Таблица истинности функции логического сложения
Истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Таблица истинности функции логического сложения
Слайд 12Логическое отрицание (инверсия)
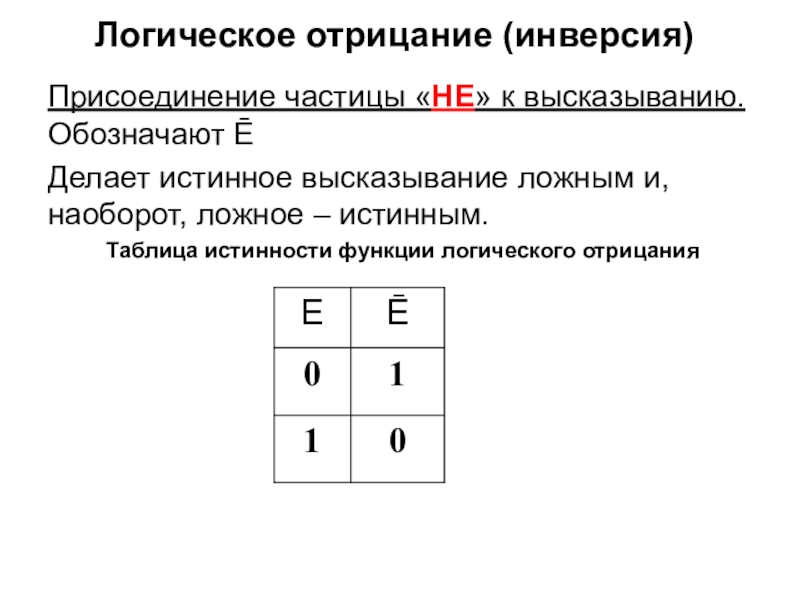
Присоединение частицы «НЕ» к высказыванию. Обозначают Ē
Делает истинное высказывание
ложным и, наоборот, ложное – истинным.
Таблица истинности функции логического отрицания
Таблица истинности функции логического отрицания
Слайд 15В обыденной и научной речи кроме базовых логических связок «и», «или»,
«не» используются и некоторые другие: «если... то...», «... тогда и только тогда, когда...» и др. Некоторые из них имеют свое название и свой символ, и им соответствуют определенные логические функции.
Слайд 16Логическое следование (импликация)
Логическое следование (импликация) образуется соединением двух высказываний в одно
с помощью оборота речи «если..., то...».
Обозначение: А →В, А В.
Пример: А={2·2=4} и В={3·3=10}.
А В={Если 2·2=4, то 3·3=10 }
Обозначение: А →В, А В.
Пример: А={2·2=4} и В={3·3=10}.
А В={Если 2·2=4, то 3·3=10 }
Слайд 17Составное высказывание, образо-ванное с помощью операции логического следования (импликации), ложно тогда
и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).
Слайд 19Например, высказывание «Если число делится на 10, то оно делится на
5» истинно, так как истинны и первое высказывание(предпосылка), и второе высказывание (вывод).
Высказывание «Если число делится на 10, то оно делится на 3» ложно, так как из истинной предпосылки делается ложный вывод.
Высказывание «Если число делится на 10, то оно делится на 3» ложно, так как из истинной предпосылки делается ложный вывод.
Слайд 20Однако операция логического следования несколько отличается от обычного понимания слова «следует».
Если первое высказывание (предпосылка) ложно, то вне зависимости от истинности или ложности второго высказывания (вывода) составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следовать что угодно.
Слайд 21Доказать методом сравнения таблиц истинности, что операция импликации А→В равносильна логическому
выражению А v В.
Слайд 23Логическое равенство (эквивалентность)
Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно
с помощью оборота речи «... тогда и только тогда, когда ...».
Обозначения: А=В; А В; А~В; А=В
А={Угол прямой}; В={Угол равен 900}
А~В ={Угол называется прямым тогда и только тогда, когда он равен 900}
Обозначения: А=В; А В; А~В; А=В
А={Угол прямой}; В={Угол равен 900}
А~В ={Угол называется прямым тогда и только тогда, когда он равен 900}
Слайд 24Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и
только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Слайд 26Рассмотрим, например, два высказывания: А = «Компьютер может производить вычисления» и
B = «Компьютер включен». Составное высказывание, полученное с помощью операции эквивалентности, истинно, когда оба высказывания либо истинны, либо ложны:
«Компьютер может производить вычисления тогда и только тогда, когда компьютер включен».
«Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен».
«Компьютер может производить вычисления тогда и только тогда, когда компьютер включен».
«Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен».
Слайд 27Составное высказывание, полученное с помощью операции эквивалентности, ложно, когда одно высказывание
истинно, а другое — ложно:
«Компьютер может производить вычисления тогда и только тогда, когда компьютер не включен».
«Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен».
«Компьютер может производить вычисления тогда и только тогда, когда компьютер не включен».
«Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен».